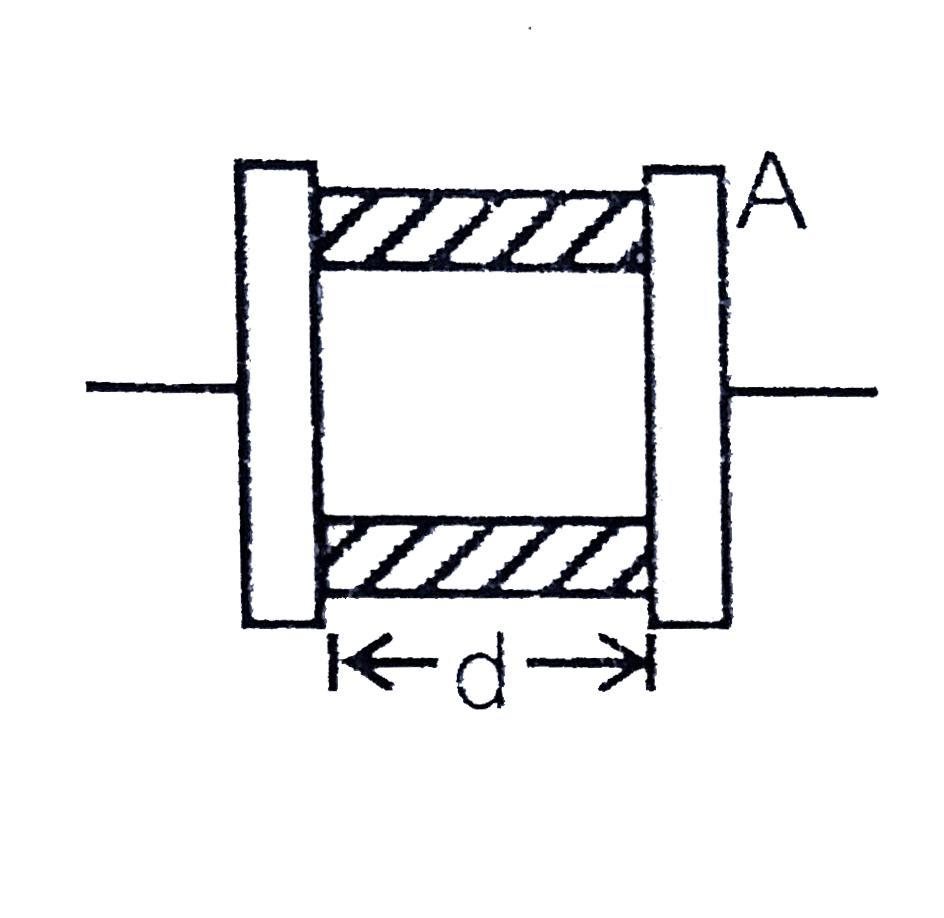
A parallel plate capacitor of area A and separation d is provided with

A parallel plate capacitor of plate area A and separation d is filled with two materials each of thickness $\frac{d}{2}$ and dielectric constants $\in_{1}$ and $\in_{2}$ respectively. The equivalent capacitance will be

A $\frac{\in_{0} A}{d} (\in_{1} + \in_{2})$
B $\frac{\in_{0} A}{d} \frac{(\in_{1} + \in_{2})}{\in_{1} \in_{2}}$
C $\frac{2 \in_{0} A}{d} \frac{\in_{1} \in_{2}}{(\in_{1} + \in_{2})}$
D $\frac{2 \in_{0} A}{d} \frac{(\in_{1} + \in_{2})}{\in_{1} \in_{2}}$
A metal plate has an area of $10 m^{2}$ . On raising its temperature by $20^{\circ} C$ . The change in area if the coefficient of linear expansion is a, will be
A $100 α$
B $200 α$
C $400 α$
D $600 α$
A fluid having a thermal coefficient of volume expansion $γ$ is filled in a cylindrical vessel up to a height $h_{0}$ . The coefficient of linear thermal expansion of the material of the vessel is $α$ . If the fluid is heated with the vessel , then find the level of liquid when temperature increases by $Δ θ$ .
A $\frac{h_{0} (1 + γ Δ θ)}{(1 + 2 α Δ θ)}$
B $\frac{h_{0} (1 + γ Δ θ)}{(1 + 3 α Δ θ)}$
C $\frac{h_{0} (1 + γ Δ θ)}{(1 + α Δ θ)}$
D $h_{0} (1 + γ Δ θ)$

The correct Answer is:C