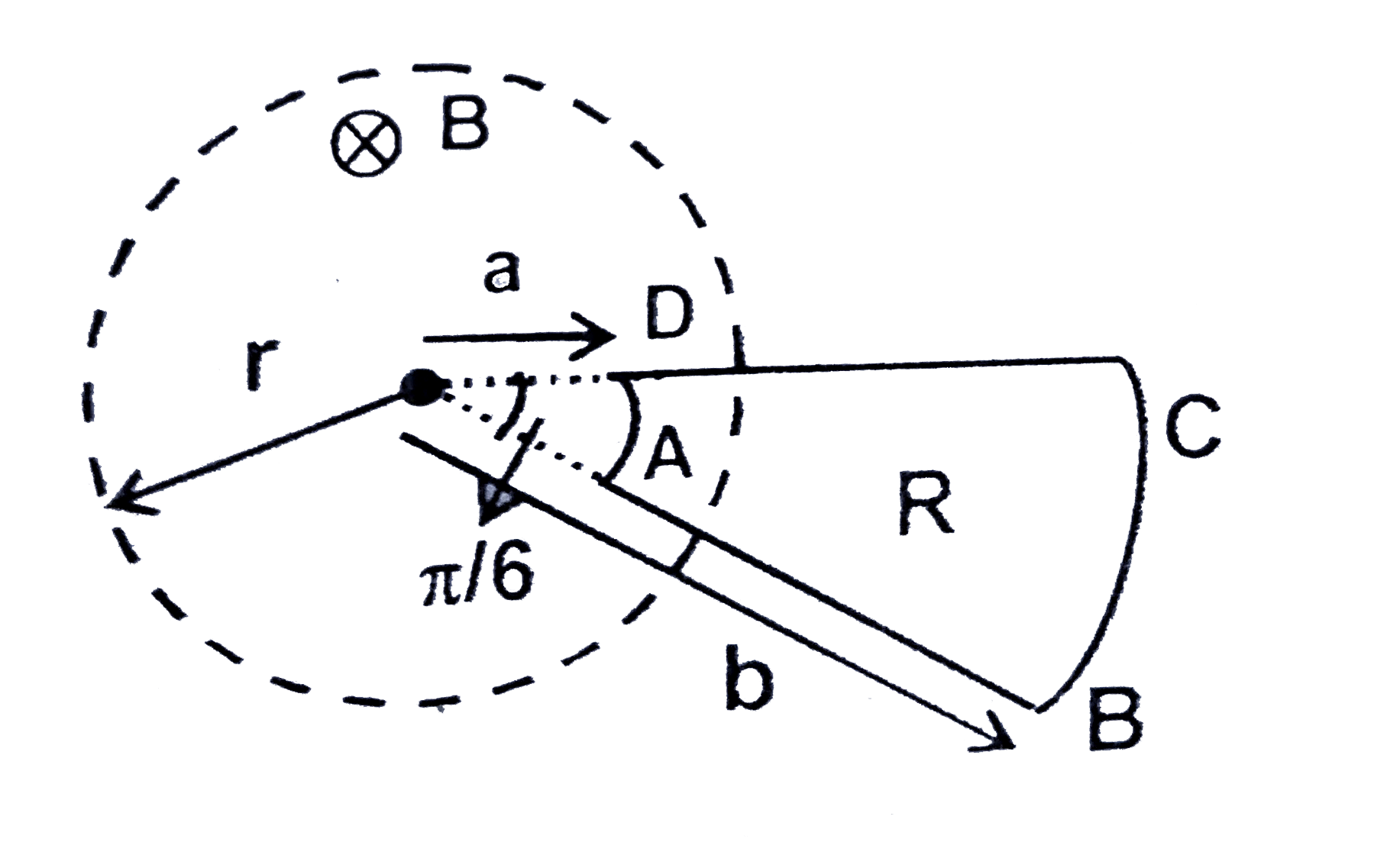
Magnetic field B in a cylindrical region of radius r varies according to the law B=B0t as shown in the figure. A fixed conducting loop ABCDA of resistance R is lying in the region as show . The current flowing through the loop is
πa2B012R
π(r2−a2)B012R
π(b2−a2)B012R
none of the above
The correct Answer is:B
e=dϕdt=(r2−a2)2π6dBdt
∴i=(r2−a2)πB012R
Topper's Solved these Questions
- TEST PAPERSBook:FIITJEEChapter:TEST PAPERSExercise:PHYSICS
Explore 747 Videos
- SIMPLE HARMONIC MOTIONBook:FIITJEEChapter:SIMPLE HARMONIC MOTIONExercise:Assignment Problems (Objective) (Level-II)
Explore 20 Videos
- WORK, ENERGY AND POWER Book:FIITJEEChapter:WORK, ENERGY AND POWER Exercise:COMPREHENSIONS ( Comprehension-II)
Explore 5 Videos
Similar Questions
A cicular current loop of radius a is placed in a radial magnetic field B as shown . The net force acting of the loop is :
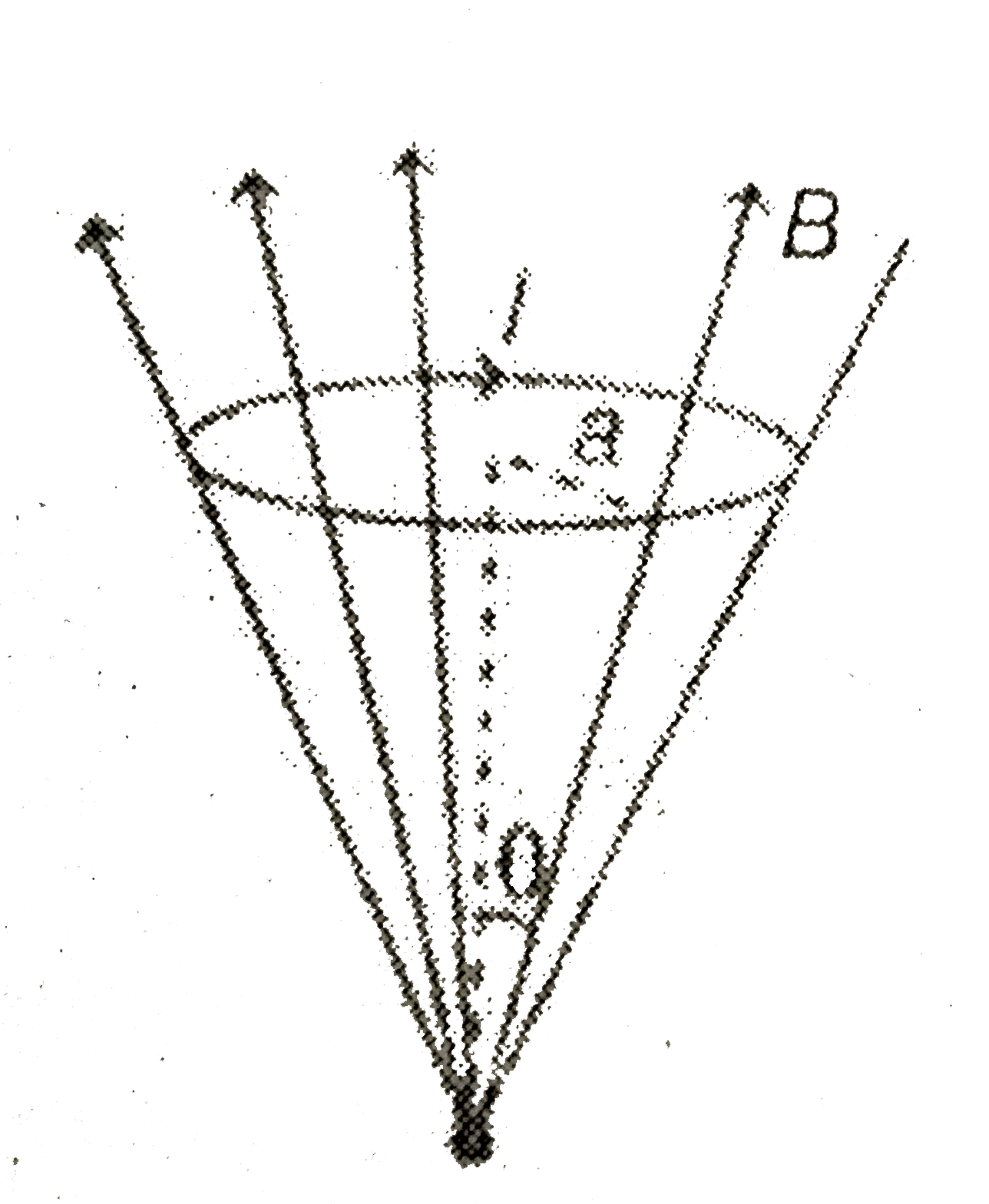
View SolutionThere exists a uniform magnetic field ¯¯¯B=B0t¯k in a region. A circular conducting loop of radius r and resistance R is placed with its plane in x-y plane. Determine the current through the loop and sense of the current.
View Solution
Knowledge Check
Magnetic field in cylindrical region of radius R in inward direction is as shown in figure.
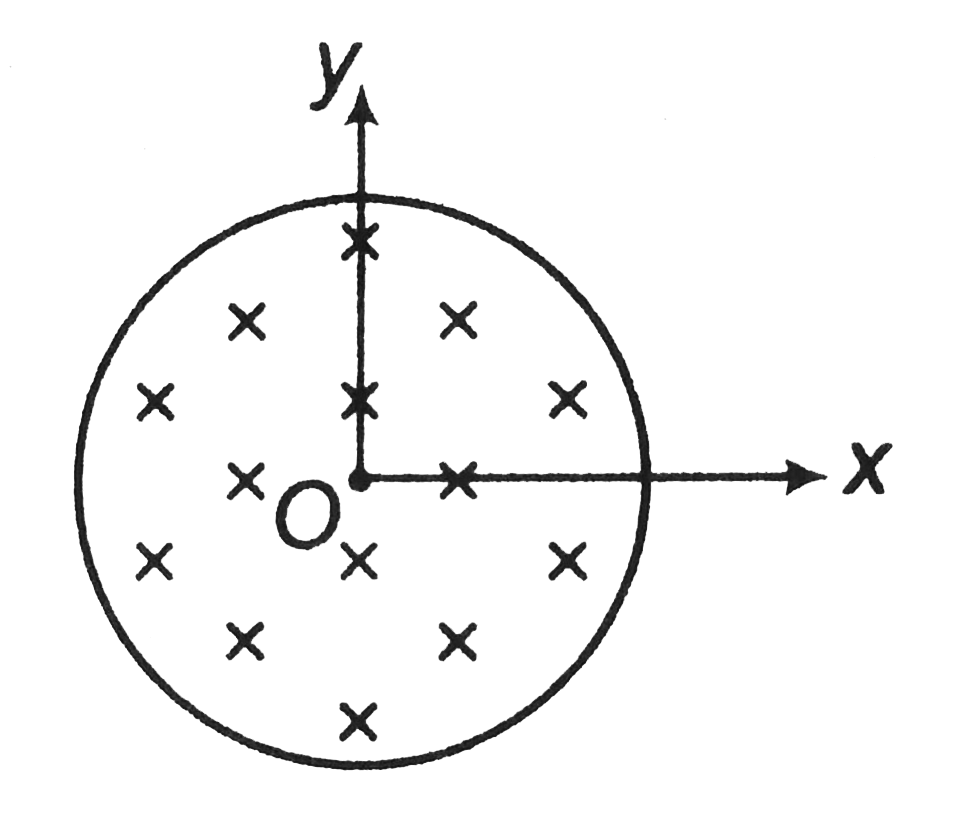 Aan electron will expereince no force kept is (2R,0,0) if magnetic field increases with timeBin the above situation, electron will experience the force in negative y-axisCif a proton is kept at (0,R2,0) and magnetic field is decreasing then it will experience the force in positive x-directionDif a proton is kept at (−R,0,0) and magnetic field is increasing then it will experience force in negative y-axis
Aan electron will expereince no force kept is (2R,0,0) if magnetic field increases with timeBin the above situation, electron will experience the force in negative y-axisCif a proton is kept at (0,R2,0) and magnetic field is decreasing then it will experience the force in positive x-directionDif a proton is kept at (−R,0,0) and magnetic field is increasing then it will experience force in negative y-axisA rod of negligible dimensions carrying a charge q falls into a conducting loop of resistance R and radius a through a height h. The current flowing through the loop will be
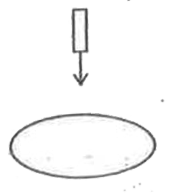 AZeroBq.(g/h)Cq√ghDq2gh
AZeroBq.(g/h)Cq√ghDq2ghA uniform but time-varying magnetic field B(t) exists in a circular region of radius a and is directed into the plane of the paper, as shown in the figure. The magnitude of the induced electric field at point P at a distance r from the centre of the circular region
 Ais zeroBdecreases as 1rCincreases as rDdecreases as 1r2
Ais zeroBdecreases as 1rCincreases as rDdecreases as 1r2
A stationary circular loop of radius a is located in a magnetic field which varies with time from t = 0 to t = T according to law B=B0t(T−t). If plane of loop is normal to the direction of field and resistance of the loop is R, calculate
magnitude of charge flown through the loop from instant t = 0 to the instant when current reverses its direction.
View SolutionA uniform but time-varying magnetic field B (t) exists in a circular region of radius a and is directed into the plane of the paper as shown . The magnitude of the induced electric field at point P at a distance r from the centre of the circular region is
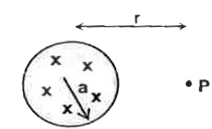
View SolutionA uniform but time varying magnetic field B(t) exists in a circular region of radius a and is directed into the plane of paper as shown. The magnitude of the induced electric field at point P at a distance r from the centre of the circular region.

View SolutionA uniform but time varying magnetic field B(t) exist in a circular region of radius a and is directed into the plane of the paper as shown. The magnitude of the induced electric field at point P at a distance r form the centre of the circular region.

View SolutionA uniform but time-varying magnetic field B(t) exists in a circular region of radius a and is directed into the plane of the paper, as shown. The magnitude of the induced electric field at point P at a distance r from the centre of the circular region
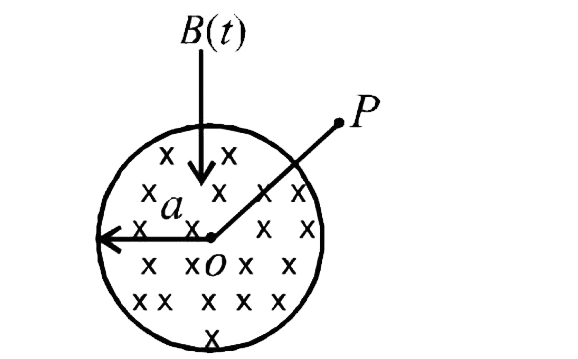
View Solution

