A hollow tube has a length l, inner radius R1 and outer radius R2 . The material has a thermal conductivity K. Find the heat flowing through the walls of the tube if
(a) the flat ends are maintained at temperature T1 and T2(T2>T1)
(b) the inside of the tube is maintained at temperature T1 and the outside is maintained at T2 .
The correct Answer is:2πKl(T2−T1)In(R2/R1)

Let an element which is hollow cyl. of Radius and width dr
dR=drK2πrlR=12πKlR2∫R1drr=12πKl
(Inr)R2R1=12πKlIn(R2R1)
iH=T2−T112πKlln(R2/R1)=2πKl(T2−T1)ln(R2/R1)
Topper's Solved these Questions
- HEAT TRANSFERBOOK - RESONANCECHAPTER - HEAT TRANSFEREXERCISE - Exercise-3
1 Videos
- HEAT TRANSFERBOOK - RESONANCECHAPTER - HEAT TRANSFEREXERCISE - Advancel Level Problems
17 Videos
- HEAT TRANSFERBOOK - RESONANCECHAPTER - HEAT TRANSFEREXERCISE - Exercise-2
1 Videos
- GRAVITATIONBOOK - RESONANCECHAPTER - GRAVITATIONEXERCISE - Exercise
21 Videos
- KINEMATICSBOOK - RESONANCECHAPTER - KINEMATICSEXERCISE - Exercise
65 Videos
Similar Questions
A spherical shell of inner radius R1 and outer radius R2 is having variable Where 'r' is the distance from the centre Two surface of the shell are maintained at temperature T1 respectively (T1<T2) The heat current flowing through the shell would be .
View SolutionFind the heat current through the frustum of a cone shown in figure-4.20. Temperature of its two ends are maintained at T1 and T2(T_(2)>T_(1)) respectively and the thermal conductivity of the material is k.
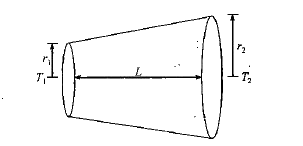
View Solution
Knowledge Check
A rod of length l and cross-section area A has a variable thermal conductivity given by K = α T, where α is a positive constant and T is temperature in kelvin. Two ends of the rod are maintained at temperature T1 and T2 (T1>T2). Heat current flowing through the rod will be
AAα(T21−T22)lBAα(T21+T22)lCAα(T21+T22)3lDAα(T21−T22)2lA slab of material has area A, thickness L, and thermal conducitivy k. One of its surface (P ) is maintained at temperature T1 and the other surface (Q ) is maintained at a lower temperature T2. The rate of heat flow from P to Q is :
AkA(T1−T2)L2BkL(T1−T2)ACkL(T1−T2)LDk(T1−T2)(LA)A solid at temperature T1 is kept in an evacuated chamber at temperature T2>T1 . The rate of increase of temperature of the body is propertional to
AT2−T1BT22−T21CT32−T31DT22−T41 .
A rod of length L with sides fully insulated is made of a material whose thermal conductivity K varies with temperature as K=αT where α is constant. The ends of rod are at temperature T1 and T2(T2>T1) Find the rate of heat flow per unit area of rod .
View SolutionA thick spherical shell of inner and outer radii r and R respectively has thermal conductivity k=ρxn , where ρ is a constant and x is distance from the centre of the shell. The inner and outer walls are maintained at temperature T1 and T2(<T1)
(a) Find the value of number n (call it n0) for which the temperature gradient remains constant throughout the thickness of the shell.
(b) For n=n0, find the value of x at which the temperature is T1+T22
(c) For n=n0, calculate the rate of flow of heat through the shell.
View SolutionTwo thin conectric shells made of copper with radius r1 and r2(r2>r1) have a material of thermal conductivity K filled between them. The inner and outer spheres are maintained at temperature TH and TC respectively by keeping a heater of power P at the centre of the two sphers. Find the value of P.
View SolutionA rod of length l with thermally insulated lateral surface is made of a material whose thermal conductivity varies as K=sc/T where c is a constant. The ends are kept at temperatures T1 and T2. Find the temperature at a distance x from te first end where the temperature is T1 and the heat flow density.
View SolutionA slab of cunductivity k is in the shape of trapezoid as shown I figure. If the two end faces be maintained at temperature T1=50∘CandT2=25∘C, then determine the thermal current through the slab by ignoring any heat loss through the lateral surfaces.
 .
.
View Solution
