A metal rod of cross sectional area 1.0cm2 is being heated at one end. At one time , the temperature gradient is 5.0∘Ccm−1 at cross section A and is 2.5∘Ccm−1 at cross section B. Calculate the rate at which the temperature is increasing in the part AB =0.40J∘C−1 , thermal conductivity of the material of the rod. =200Wm−1^(@)C^(-1) . Neglect any loss of heat to the atmosphere.
The correct Answer is:12∘C/s

(dTdx)A=5(dTdx)=2.6I=ΔTL(KA)
iA=(dTdx)AKAiB=(dTdx)BKA
I=(dQdt)Absorb=[(dTdx)A−(dTdx)B]KA=msdθdt
(5−2.6)×200×(1×10−2)=msdθdt
2.4×2=msdθdt=4.8
ms=0.4J/Cdθdt=4.80.4=12∘C/s
Topper's Solved these Questions
- HEAT TRANSFERBOOK - RESONANCECHAPTER - HEAT TRANSFEREXERCISE - Exercise-3
1 Videos
- HEAT TRANSFERBOOK - RESONANCECHAPTER - HEAT TRANSFEREXERCISE - Advancel Level Problems
17 Videos
- HEAT TRANSFERBOOK - RESONANCECHAPTER - HEAT TRANSFEREXERCISE - Exercise-2
1 Videos
- GRAVITATIONBOOK - RESONANCECHAPTER - GRAVITATIONEXERCISE - Exercise
21 Videos
- KINEMATICSBOOK - RESONANCECHAPTER - KINEMATICSEXERCISE - Exercise
65 Videos
Similar Questions
A metal rod of cross sectional area 1.0cm2 is being heated at one end. At one time , the temperature gradient is 5.0∘Ccm−1 at cross section A and is 2.5∘Ccm−1 at cross section B. calculate the rate at which the temperature is increasing in the part AB of the rod. The heat capacity of the part AB=0.40J∘C−1 , thermal conductivity of the material of the rod. K=200Wm−1C−1 . Neglect any loss of heat to the atmosphere.
View SolutionFind the rate of heat flow through a cross section of the rod shown in figure (θ2>θ1 . Thermal conductivity of the material of the rod is K.

View Solution
Knowledge Check
An irregular rod of same uniform material as shown in is conducting heat at a steady rate. The temperature gradient at varoius sections versus area of cross section graph will be
 .A
.A B
B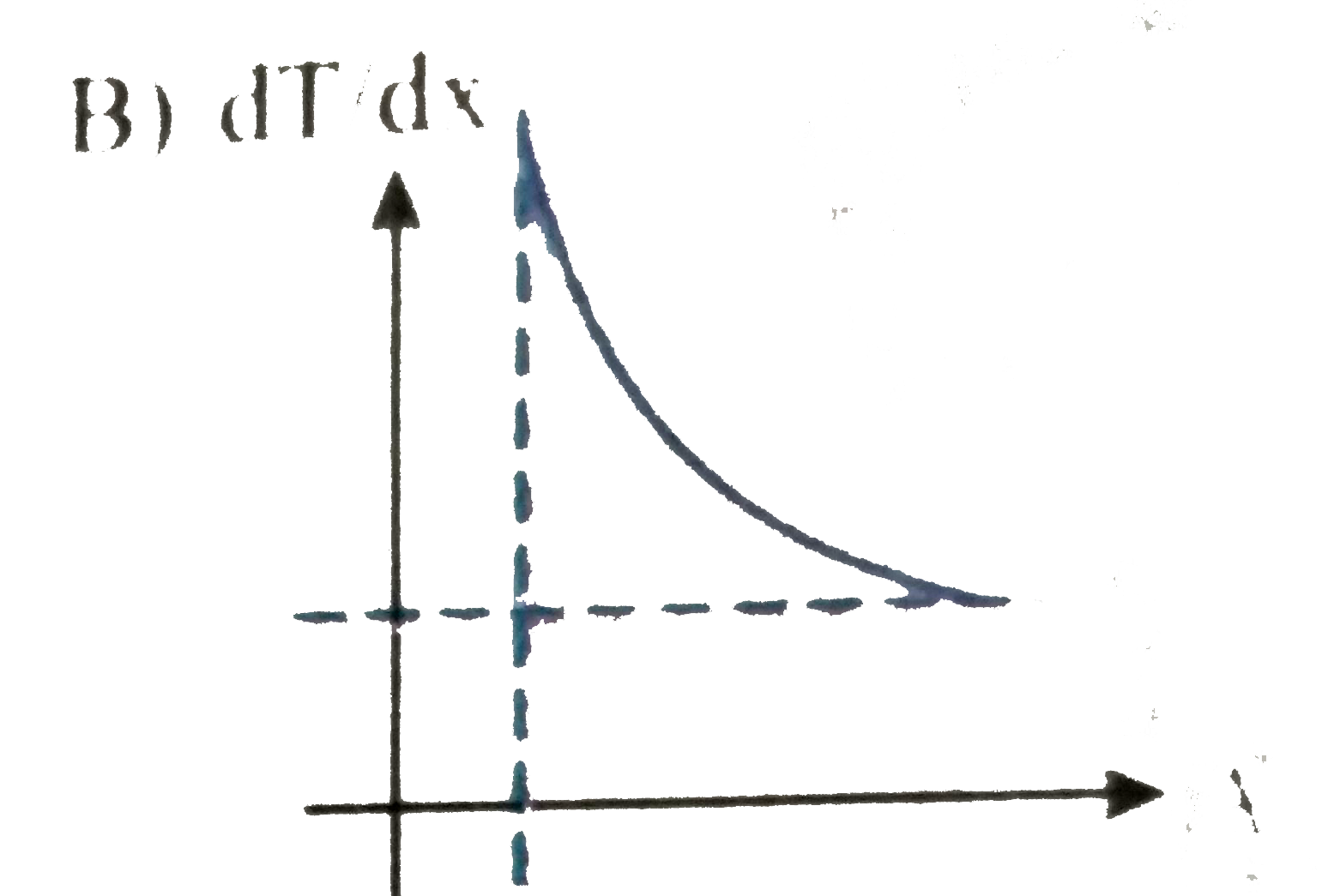 C
C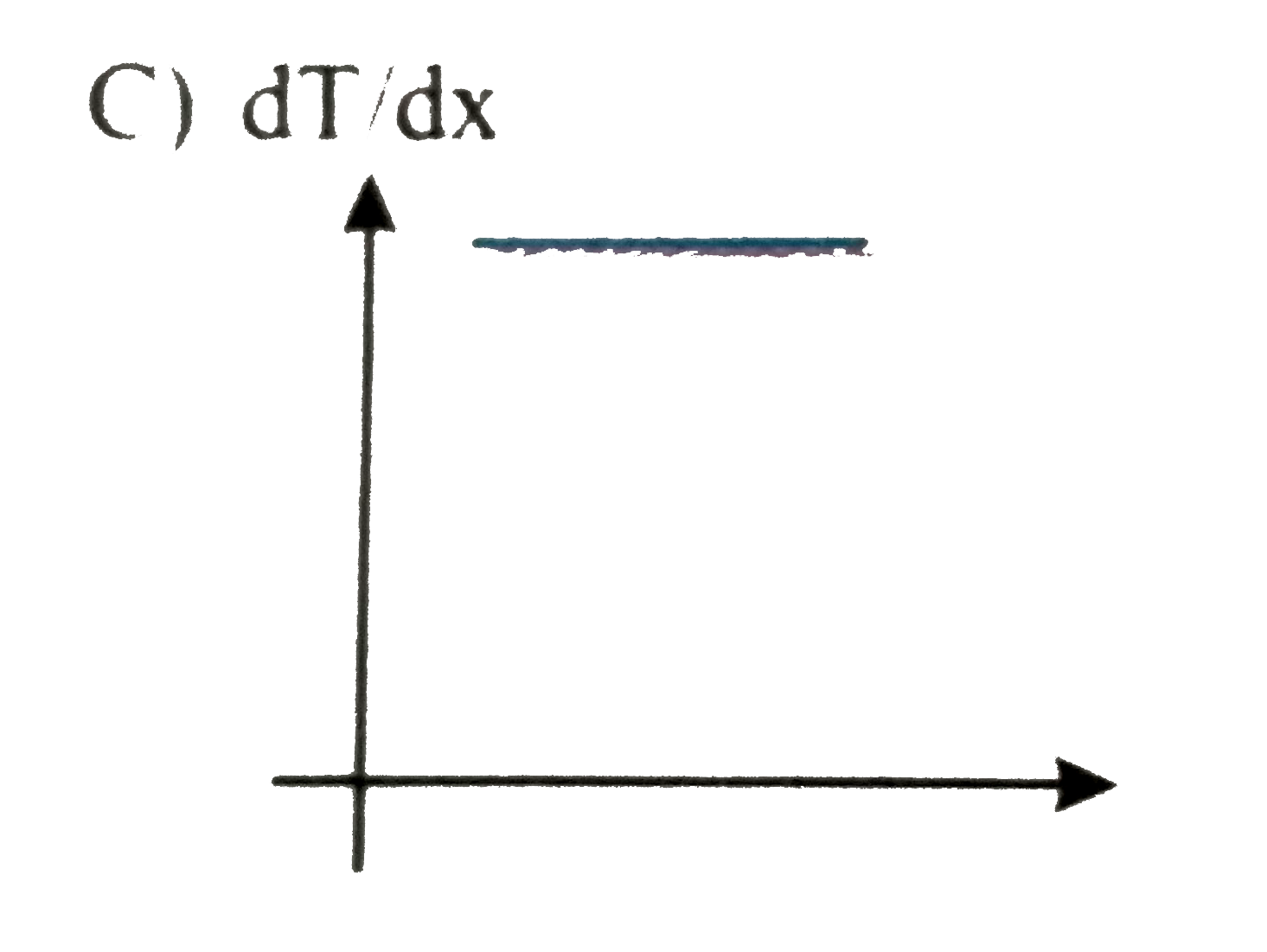 D
D
One end of a metal rod of length 1.0 m and area of cross section 100cm2 is maintained at . 100∘C. If the other end of the rod is maintained at 0∘C , the quantity of heat transmitted through the rod per minute is (Coefficient of thermal conductivity of material of rod =100W/m−K)
A3×103JB6×103JC9×103JD12×103JAn irregular rod of same uniform material as shown in figure is conducting heat at a steady rate. The temperature gradient at various sections versus area of cross section graph will be
_S01_094_Q01.png) A
A_S01_094_O01.png) B
B_S01_094_O02.png) C
C_S01_094_O03.png) D
D_S01_094_O04.png)
A rod of length1m having cross sections area 0.75m^(2), conducts heat at 6000J/sec.Then the temperature difference across the rod isK=200Wm^(-1)k^(-1)
View SolutionCalculate the thermal resistance of an aluminium rod of length 20cm and area of cross-section 4cm2. The thermal conductivity of aluminium is 210Js−1m−1K−1.
View SolutionAn aluminium rod and a copper rod of equal length 1.0m and cross-sectional area. 1cm2 are welded together as shown in figure. One end is kept at a temperature of 20∘C and the other at 60∘C Calculate the amount of heat taken out per second from the hot end. thermal conuctivity of aluminium =200Wm−1^(@)C^(-1)andofcopper=390Wm^(-1)^(∘)C−1 .

View SolutionThree rods of material x and three of material y are connected as shown in figure. All the rods are identical in length and cross sectional area. If the end A is maintained at 60∘C and the junction E at 10∘C , calculate the temperature of the junction B. The thermal conductivity of x is 800Wm−1^(@)C^(-1)andtˆofyis400Wm^(-1)^(∘)C−1 .

View Solutionmeter rod of area of cross section 4mc2 with K=0.5calg−1C−1 is observed that at steady state 360 cal of heat flows per minute The temperature gradient along the rod is .
View Solution
