A slab of cunductivity k is in the shape of trapezoid as shown I figure. If the two end faces be maintained at temperature T1=50∘CandT2=25∘C, then determine the thermal current through the slab by ignoring any heat loss through the lateral surfaces.
 .
.
i=30kln(85)J/s
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBook:AAKASH INSTITUTEChapter:THERMAL PROPERTIES OF MATTERExercise:Assignment (Section-I) Subjective Type Questions
Explore 5 Videos
- TEST 9Book:AAKASH INSTITUTEChapter:TEST 9Exercise:EXAMPLE
Explore 61 Videos
- THERMODYNAMICSBook:AAKASH INSTITUTEChapter:THERMODYNAMICSExercise:ASSIGNMENT (SECTION -D) (Assertion - Reason Type Questions)
Explore 10 Videos
Similar Questions
A hollow tube has a length l, inner radius R1 and outer radius R2 . The material has a thermal conductivity K. Find the heat flowing through the walls of the tube if (a) the flat ends are maintained at temperature T1 and T2(T_(2)gtT_(1)(b)the∈softhetubeisma∫a∈edattemperatureT_(1)andtheoutsisma∫a∈edatT_(2) .
View SolutionFind the heat current through the frustum of a cone shown in figure-4.20. Temperature of its two ends are maintained at T1 and T2(T_(2)>T_(1)) respectively and the thermal conductivity of the material is k.
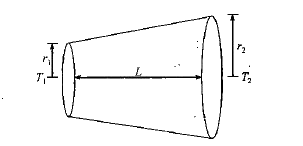
View Solution
Knowledge Check
A thin piece of thermal conductor of constant thermal conductivity insulated on the lateral sides connects two reservoirs which are maintained at temperatures T1 and T2 as shown. Assuming that the system is in steady state, which of the following plots best represents the dependence of the rate of change of entropy of the ratio of temperatures T1/T2
 A
A B
B C
C D
D
Two bars of equal length and the same cross-sectional area but of different thermal conductivities,k1 and k2, are joined end to end as shown in figure-4.36. One end of the composite bar is maintained at temperature Th whereas the opposite end is held at Tc.
If there are no heat losses from the sides of the bars, the temperature Tj of the junction is given by :
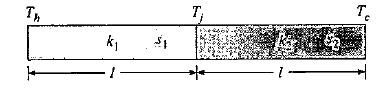 Ak2k1(Th+Tc)2Bk2k1+k2(Th+Tc)Ck1+k2k2(Th+Tc)2D1k1+k2(k1Th+k2Tc)
Ak2k1(Th+Tc)2Bk2k1+k2(Th+Tc)Ck1+k2k2(Th+Tc)2D1k1+k2(k1Th+k2Tc)A rod of length l and cross-section area A has a variable thermal conductivity given by K = α T, where α is a positive constant and T is temperature in kelvin. Two ends of the rod are maintained at temperature T1 and T2 (T1>T2). Heat current flowing through the rod will be
AAα(T21−T22)lBAα(T21+T22)lCAα(T21+T22)3lDAα(T21−T22)2l
Four thin identical rods AB,AC,BD and EF made of the same material are joined as shown. The free-ends C,D and F are maintained at temperature T1,T2 and T3 respectively. Assuming that there is no loss of heat of the surroundings, the temperature at joint E when the steady state is attained is 1K(2T1+2T2+3T3). Find K(E is mid point of AB)
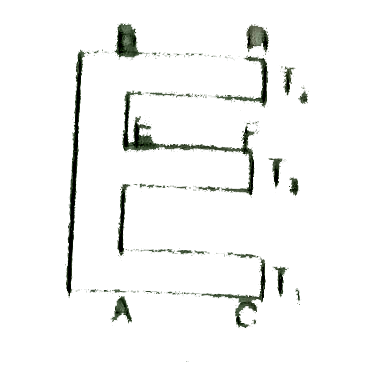
View SolutionA composite cylinder is made of two materials having thermal conductivities K1 and K2 as shown. Temperature of the two flat faces of cylinder are maintained at T1 and T2. For what ratio K1/K2 the heat current throught the two materials will be same. Assume steady state and the rod is lagged (insulated from the curved surface).
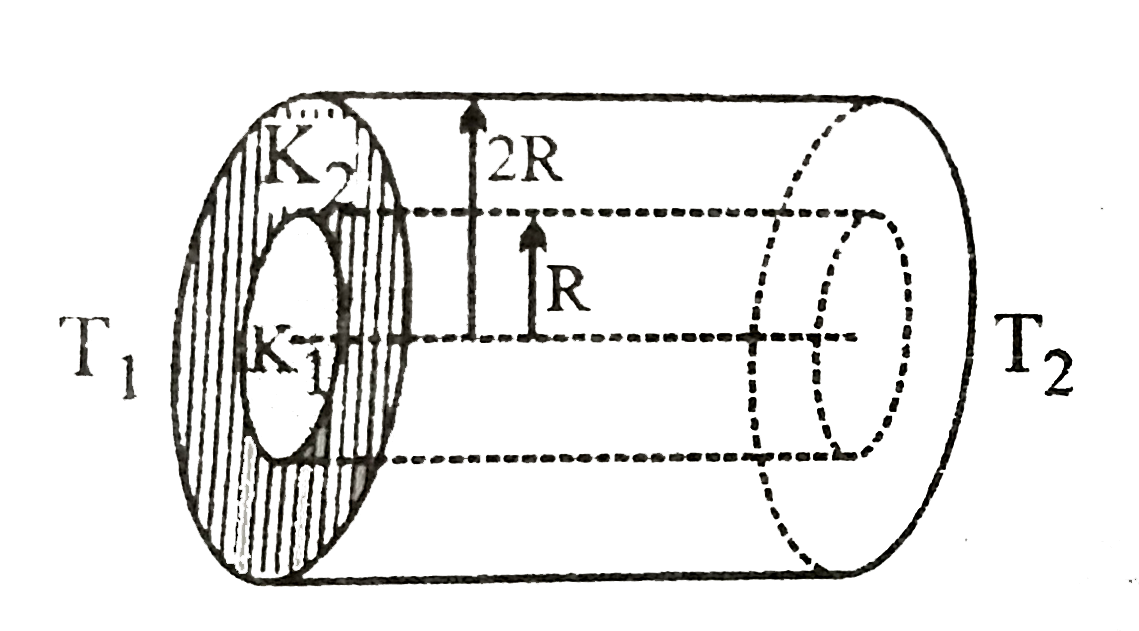
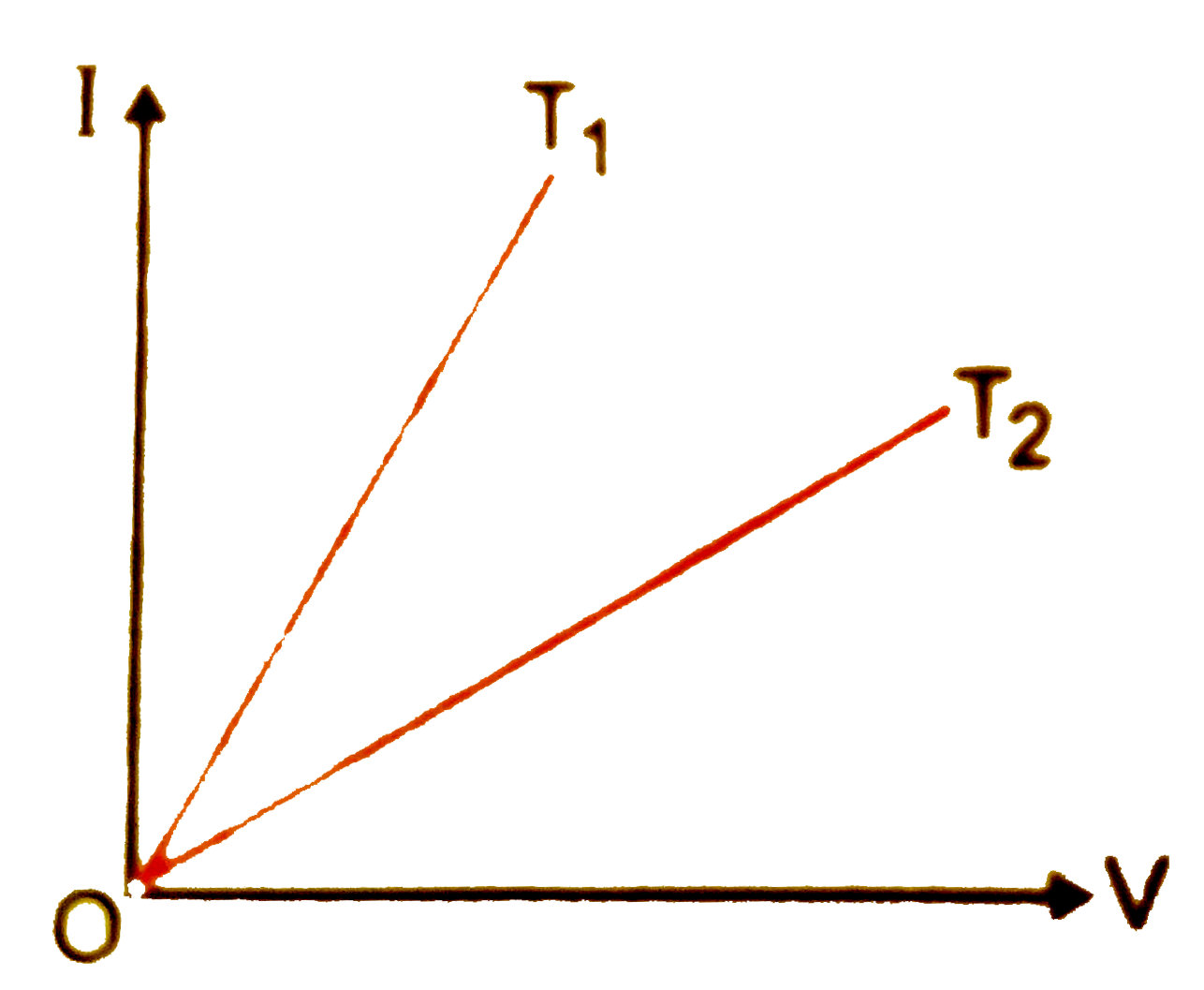
View SolutionV- I graph for a metallic wire at two different temperature T1 and T2 is shown in figure. Which of the two temperature is higher and why?
View SolutionThree rods of equal length, area of cross section and thermal conductivity are connected as shown in the figure.

There is no heat loss through lateral surface of the rods and temperature of ends are TA=100∘C,TB=70∘C and TC=50∘C. Find the temperature of junction.
View SolutionTwo ends of a rod of non uniform area of cross section are maintained at temperature T1and T2 (T1>T2) as shown in the figure
If l is heat current through the cross-section of conductor at distance x from its left face, then the variation of l with x is best represented by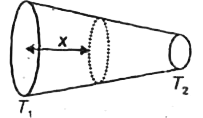
View Solution

