Three rods of equal length, area of cross section and thermal conductivity are connected as shown in the figure.

There is no heat loss through lateral surface of the rods and temperature of ends are TA=100∘C,TB=70∘C and TC=50∘C. Find the temperature of junction.
The correct Answer is:73.3∘C
Step by step video, text & image solution for Three rods of equal length, area of cross section and thermal conductivity are connected as shown in the figure. There is no heat loss through lateral surface of the rods and temperature of ends are T_(A)=100^(@)C, T_(B)=70^(@)C and T_(C)=50^(@)C. Find the temperature of junction. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- HEAT AND TEMPERATUREBook:FIITJEEChapter:HEAT AND TEMPERATUREExercise:ASSIGNMENT PROBLEMS (SUBJECTIVE) (level-1) (FILL IN THE BLANKS)
Explore 5 Videos
- HEAT AND TEMPERATUREBook:FIITJEEChapter:HEAT AND TEMPERATUREExercise:ASSIGNMENT PROBLEMS (SUBJECTIVE) (level-1) (TRUE OR FALSE QUESTIONS)
Explore 6 Videos
- HEAT AND TEMPERATUREBook:FIITJEEChapter:HEAT AND TEMPERATUREExercise:EXERCISE
Explore 9 Videos
- GRAVITATIONBook:FIITJEEChapter:GRAVITATIONExercise:Numerical based Question
Explore 2 Videos
- KINEMATICSBook:FIITJEEChapter:KINEMATICSExercise:NUMERICAL BASED QUESTIONS DECIMAL TYPE
Explore 5 Videos
Similar Questions
Three rods of same material and of equal cross sectional area and length have been connected together as shown in the figure. The temperature of the junction of the rods approximately is
View SolutionThree rods of material X and three rods of material Y are connected as shown in the figure. All the rods are of identical length and cross-sectional area. If the end A is maintained at 60∘C and the junction E at 10∘C. Calculate the temperature of the junction B, C and D. The thermal conductivity of X is 0.92cal/sec−cm∘C and that of Y is 0.46cal/sec−cm−∘C.

View Solution
Knowledge Check
Two similar rods are joined as shown in figure. Then temperature of junction is (assume no heat loss through lateral surface of rod and temperatures at the ends are shown in steady state )
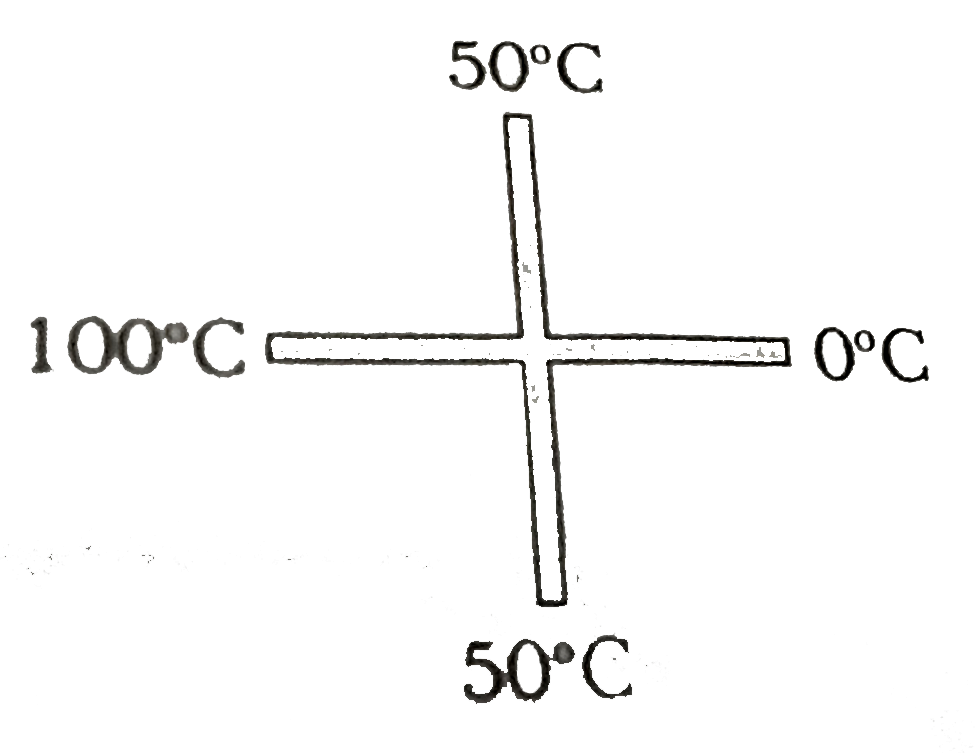 A50∘CB75∘CC66.6∘CD33.3∘C
A50∘CB75∘CC66.6∘CD33.3∘CTwo bars of same length and same cross-sectional area but of different thermal conductivites K1 and K2 are joined end to end as shown in the figure. One end of the compound bar it is at temperature T1 and the opposite end at temperature T2 (whereT1>T2). The temperature of the junction is
 AK1T1+K2T2K1+K2BK1T2+K2T1K1+K2CK1(T1+T2)K1+K2DK2T1+T2K1
AK1T1+K2T2K1+K2BK1T2+K2T1K1+K2CK1(T1+T2)K1+K2DK2T1+T2K1Two rods of similar area of cross section and length are joined as shown in the figure. The ratio of their thermal conductivity is 2:3. The free ends are maintained at 100∘C and 0∘C respectivley. THE temperature at junction in steady state is
 A50∘CB40∘CC60∘D80∘C
A50∘CB40∘CC60∘D80∘C
Three rods of material x and three of material y are connected as shown in figure. All the rods are identical in length and cross sectional area. If the end A is maintained at 60∘C and the junction E at 10∘C , calculate the temperature of the junction B. The thermal conductivity of x is 800Wm−1^(@)C^(-1)andtˆofyis400Wm^(-1)^(∘)C−1 .

View SolutionSeven identical rods of matrical of thermal conductivity k are connected as shown in All the rod are of identical length l and cross sectional area A if the one end b is kept at 100∘C and the other end is kept at 0∘C The temperatures of the junctions C,D and E(θDandθE) be in the steady state
 .
.
View SolutionSeven identical rods of material of thermal conductivity K are connected as shown in figure. All the rods are of identical length L and cross sectional area A1. If one end A is kept at 100∘C and the other end B is kept at 0∘C, what would be the temperature of the junctions C, D and E (TC,TD and TE) in the steady state?

View SolutionThree rods of the same dimensions have thermal conductivities 3k , 2k and k . They are arranged as shown, with their ends at 100∘C,50∘C and 0∘C. The temperature of their junction is :-
_E01_022_Q01.png)
View SolutionThree rods A,B and C of the same length and cross- sectional area are joined in series as shown. The temperature at the junction of A and B, in equilibriu, is
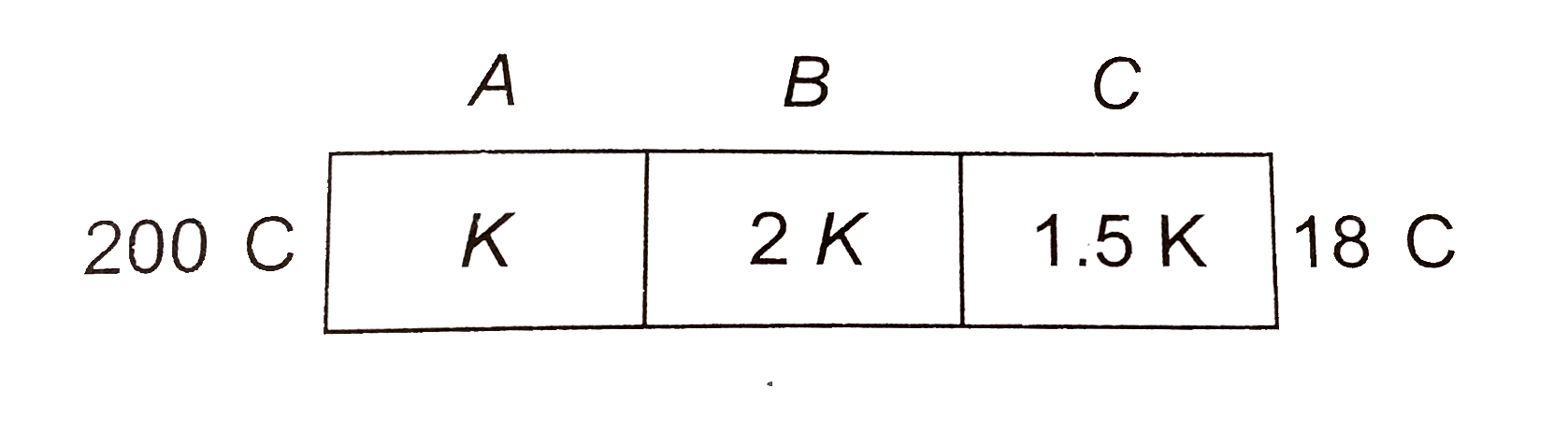
View Solution

