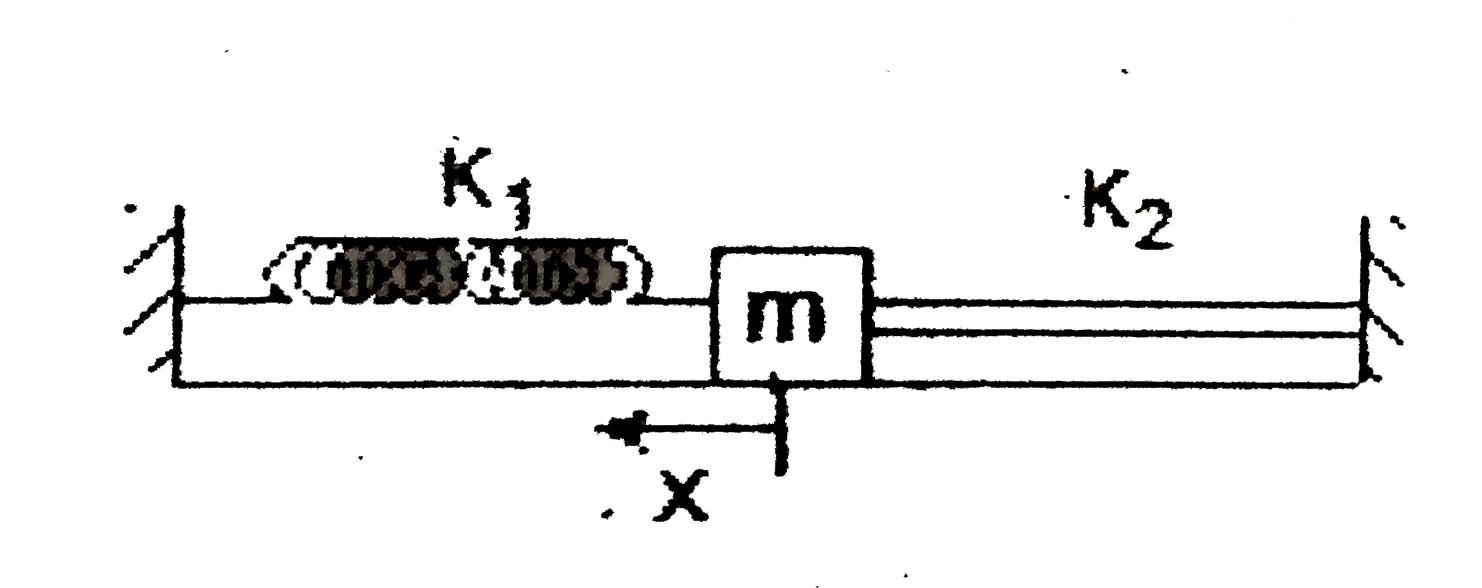
A block of mass is connected to an ideal spring of stiffness on left hand side and to an elastic strig of stiffness on right hand side as shown in figure the time period of motion if mass m is displaced by 'x' as shown in figure.
The correct Answer is:D
Note string becomes slack when mass pushes te string.
Topper's Solved these Questions
- TEST PAPERSBook:FIITJEEChapter:TEST PAPERSExercise:PHYSICS
Explore 747 Videos
- SIMPLE HARMONIC MOTIONBook:FIITJEEChapter:SIMPLE HARMONIC MOTIONExercise:Assignment Problems (Objective) (Level-II)
Explore 20 Videos
- WORK, ENERGY AND POWER Book:FIITJEEChapter:WORK, ENERGY AND POWER Exercise:COMPREHENSIONS ( Comprehension-II)
Explore 5 Videos
Similar Questions
Two identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View SolutionA block of mass m is relesed from rest from a height h onto a smooth sledge of mass M fitted with an ideal spring of stiffness k.

View Solution
Knowledge Check
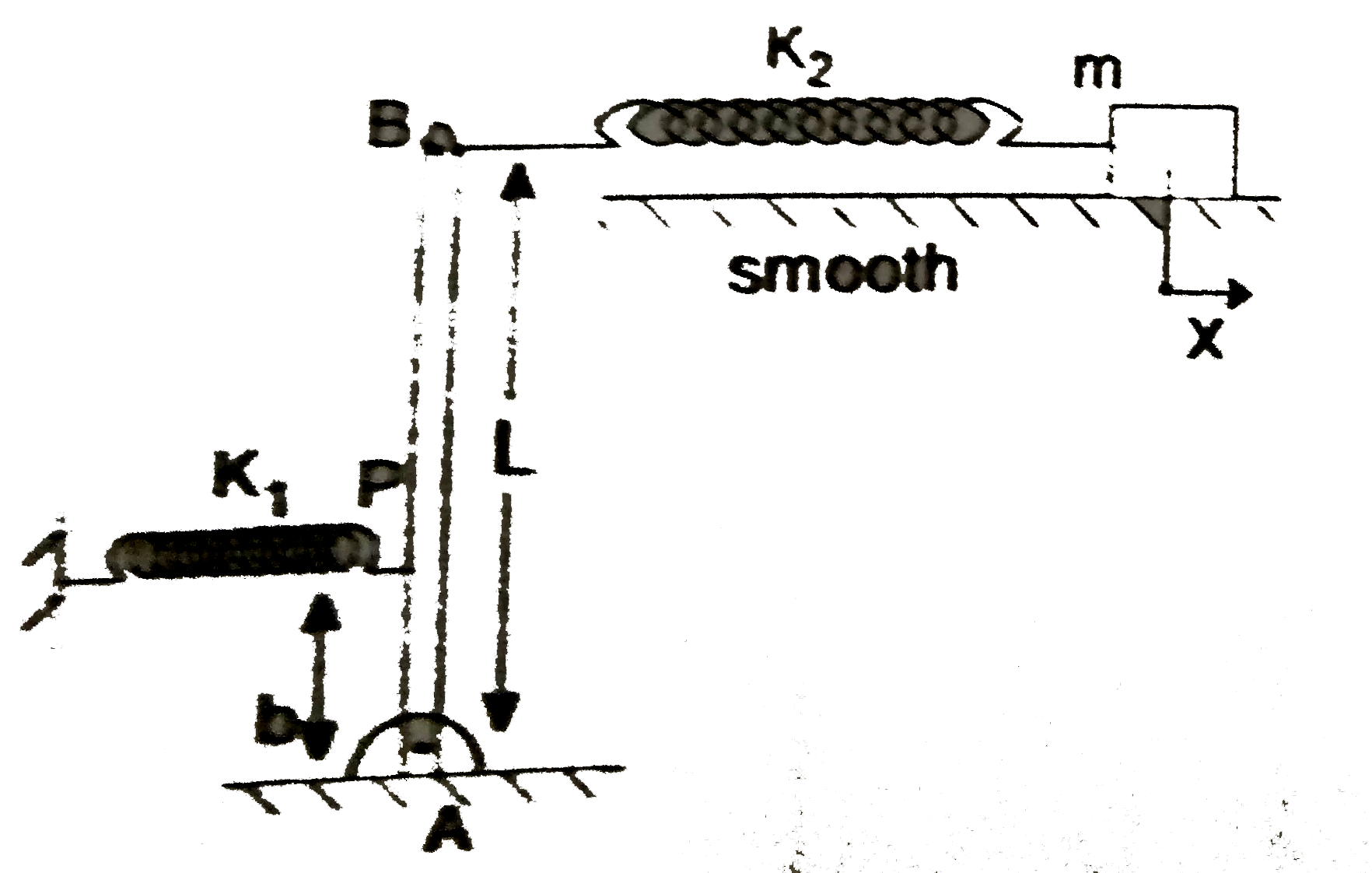
A massless Rod AB is hinged at point A. At point P, it is connected by a spring of stiffness K1 and at point B it is connected to another spring of stiffness K2 connected to mass m as shown in figure the length of Rod AB is l and displaced by a distance x from its mean position as shown in figure then the time period of S.H.M. of mass isA2π√m(K2b2+K1L2)K1K2b2B2π√m(K2L2+K1b2)K1K2b2C2π√m(K1K2b2)K2b2+K1L2D2π√m(K2L2+K1b2)K2b2A block of mass m is connected to two indentical springs of spring constant k which are in turn connected to fixed supports as shown in the figure. Find the time period for small oscillations of the block.
 A2π√mkB2π√m2kC2π√2mkDπ√m2k
A2π√mkB2π√m2kC2π√2mkDπ√m2kA spring of spring constant K is cut equal parts of which t part are places in particle and connected will mass m shown in figure The time period of oscilation motion of mass m is
AT=2π√mnrkBT=2π√nrmKCT=2π√rmnKDT=2π√nmrK
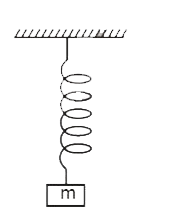
A mass m is attached to the free end of a massless spring of spring constant k with its other end fixed to a rigid support as shown in figure. Find out the time period of the mass, if it is displaced slightly by an amount x downward.
View SolutionA disc of mass m is connected with an ideal spring of stiffness k. If it is released from rest, it rolls without sliding on an inclination plane. The maximum elongation of the spring is:

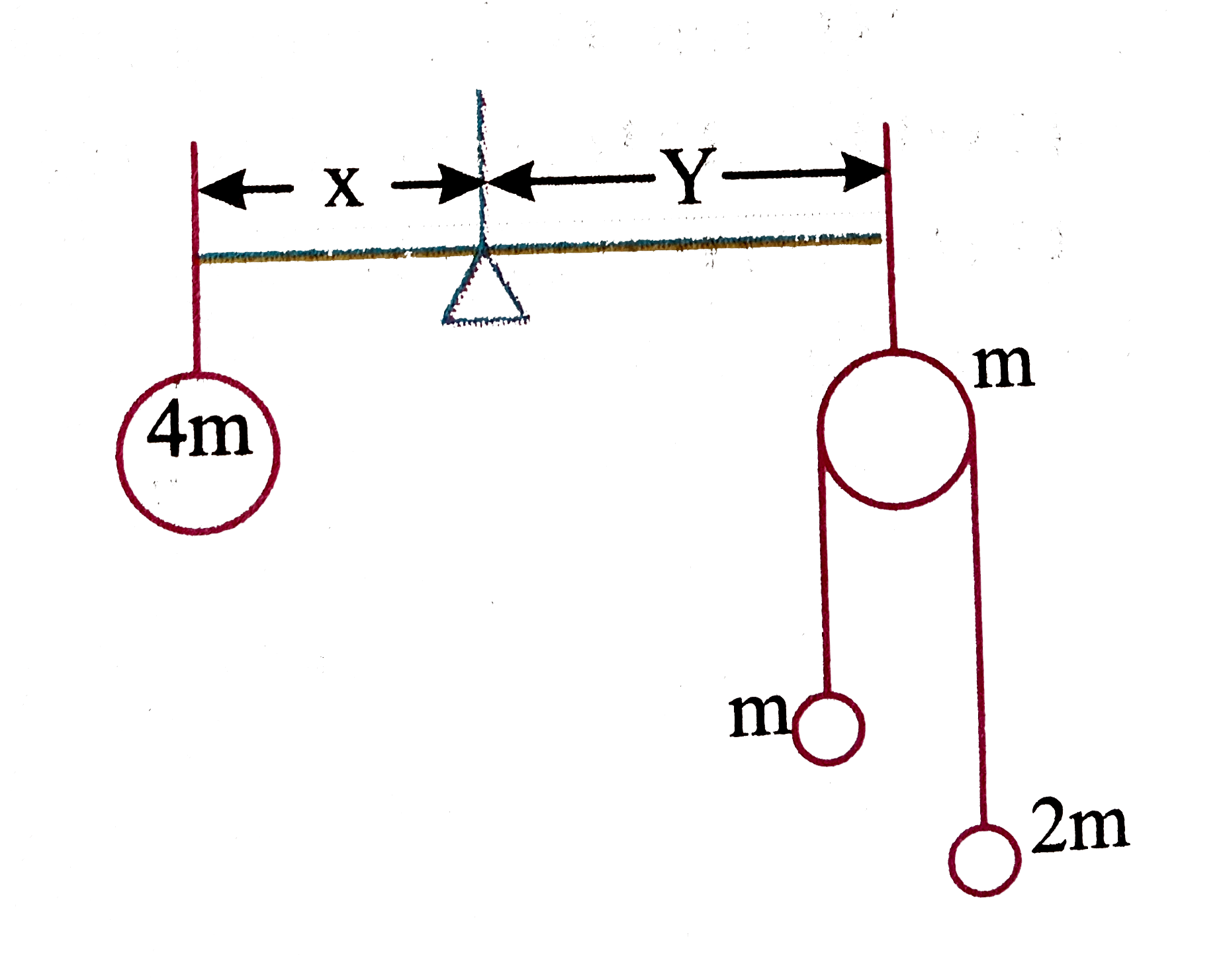
View SolutionA rigid massless beam is balanced by a particle of mass 4m in left hand side and a pulley particle system in right hand side. The value of xy is
View SolutionA block of mass m is suspended by different springs of force constant shown in figure.

View SolutionA spring of spring constant k is cut into n equal parts, out of which r parts are placed in parallel and connected with mass M as shown in figure. The time period of oscillatory motion of mass M is:

View Solution