![A planet of mass m moves in an elliptical orbit around sun with sun at its Focus. (e=eccentricity of ellipse). Then T(ACB)//T(BDA) is [T(ACB) is time taken to travel from A to C B & T(BDA) is time taken to travel from B to D to A]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/FIT_JEE_CRT_P3_E01_305_Q01.png)
A planet of mass m moves in an elliptical orbit around sun with sun at its Focus. (e=eccentricity of ellipse). Then TACB/TBDA is [TACB is time taken to travel from A to C B & TBDA is time taken to travel from B to D to A]
(π+2e)/(π−2e)
1
(π+e)/(π−e)
π/(π−1)
The correct Answer is:A
∵dAdt={Kepler's 2nd law]
∴T1T2=A1A2=πab2+12×2b×aeπab2−12×2b×ae
or T1T2=(π+2e)(π−2e)

Topper's Solved these Questions
- TEST PAPERSBOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS
747 Videos
- SIMPLE HARMONIC MOTIONBOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)
20 Videos
- WORK, ENERGY AND POWER BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)
5 Videos
Similar Questions
The figure shows the motion of a planet around the sun in an elliptical orbit with the sun at one focus. The shaded area SAB is twice that of SCD. If t1andt2 are the times taken by the planet to move from A to B and C to D respectively, then

View Solution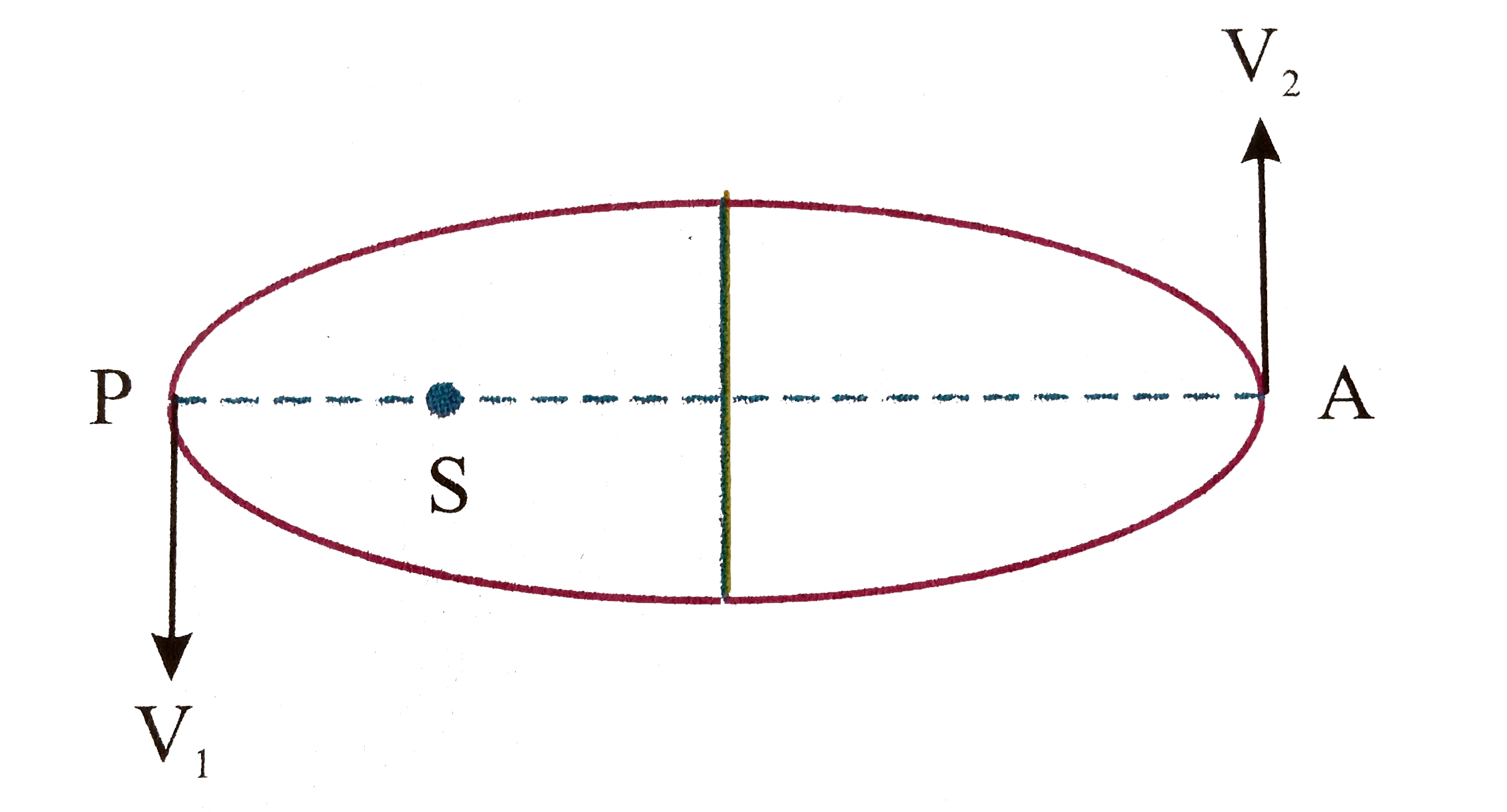
A planet of mass m is moving in an elliptical orbit around the sun of mass M. The semi major axis of its orbit is a, eccentricity is e.
Find total energy of planet interms of given parameters.
View Solution
Knowledge Check
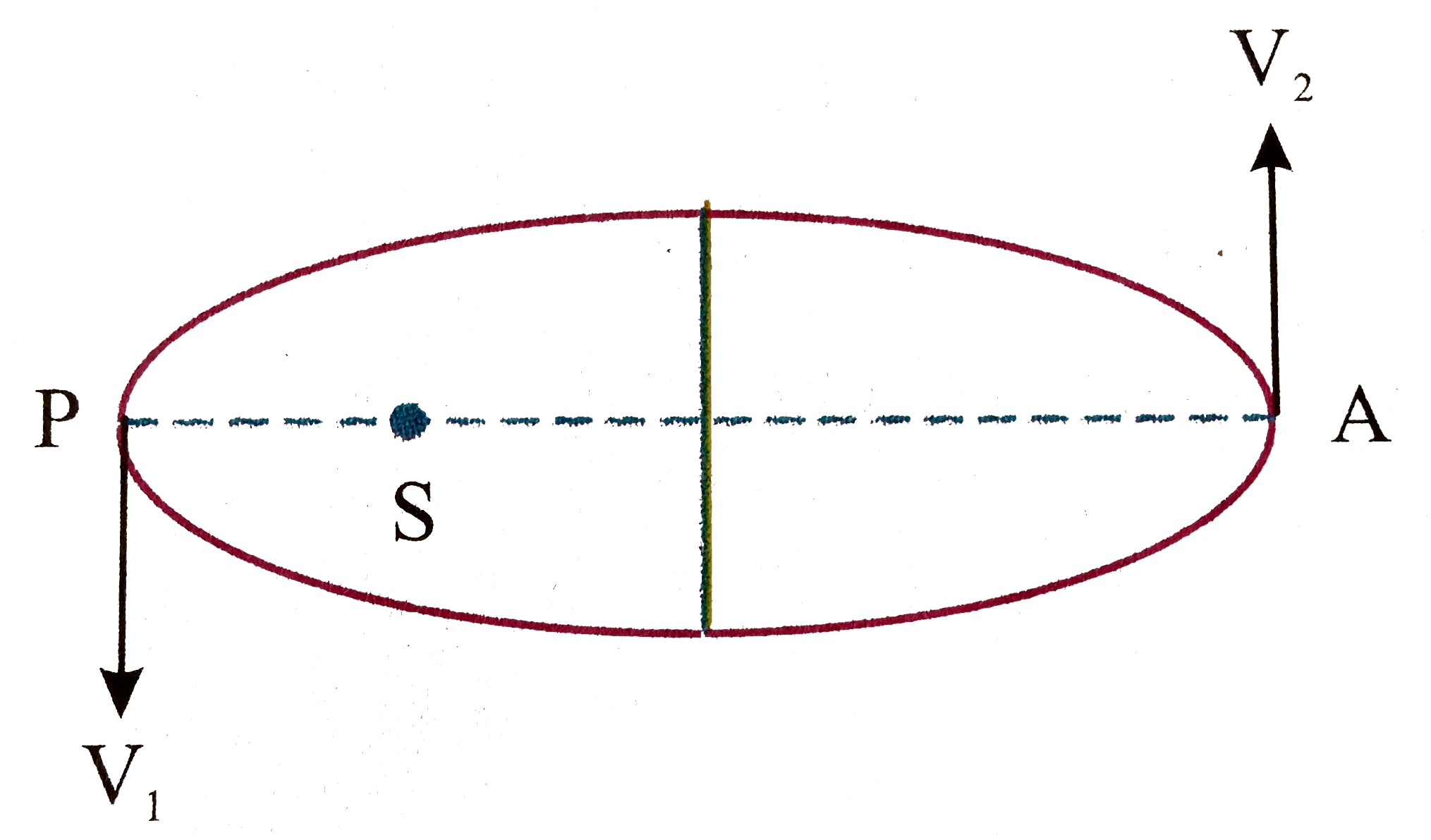
A planet of mass m is moving in an elliptical orbit around the sun of mass M. The semi major axis of its orbit is a, eccentricity is e.
Find speed of planet V2 at aphelion A.A√GMa(1+e)(1−e)B√GMa(1−e)(1+e)C√GMa3(1+e2)(1−e2)D√GMa3(1−e2)(1+e2)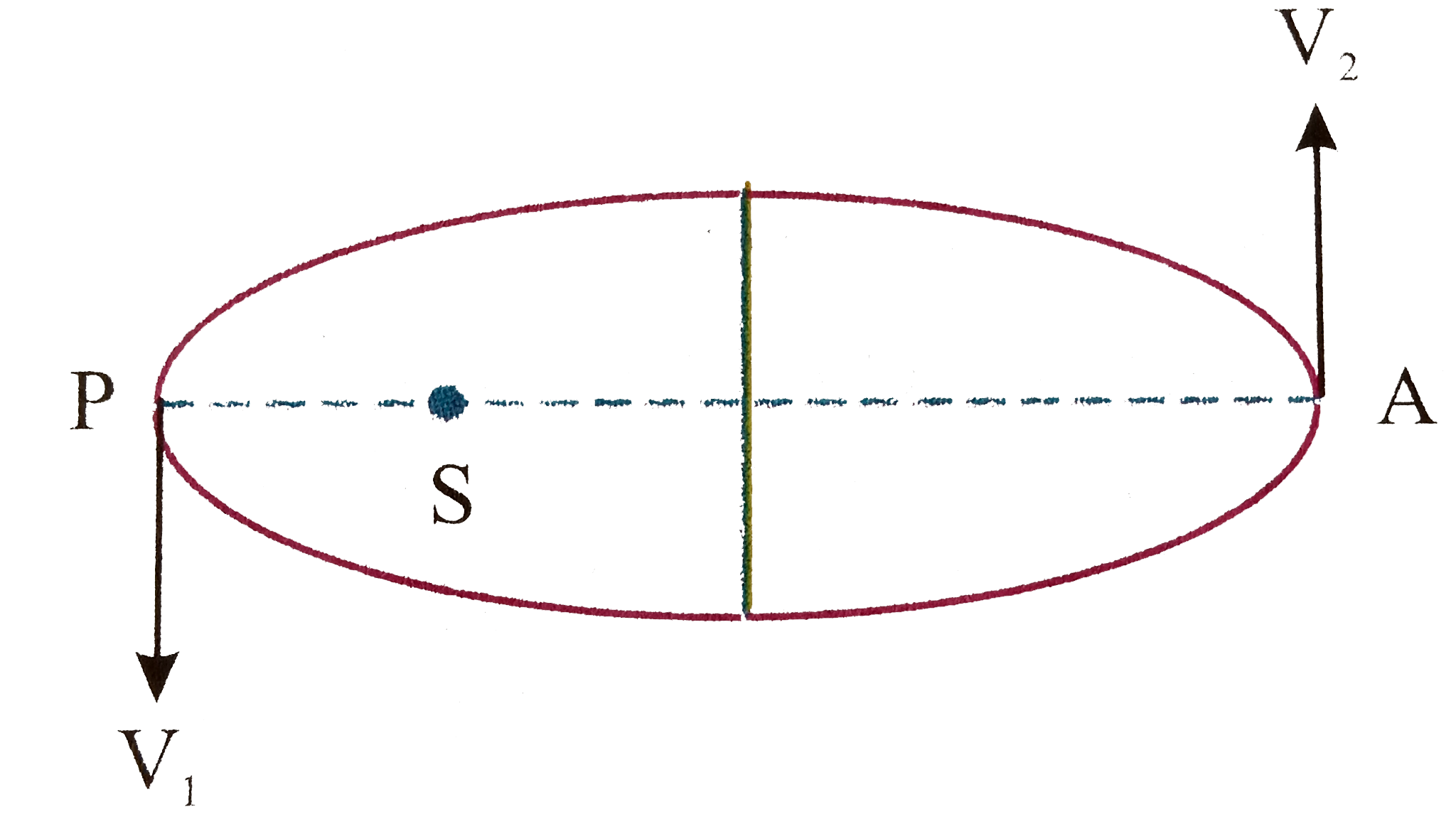
A planet of mass m is moving in an elliptical orbit around the sun of mass M. The semi major axis of its orbit is a, eccentricity is e.
Find speed of planet V1 at perihelion PA√GMa(1+e)(1−e)B1+e1−e√GMaC√GMa3(1+e)(1−e)D√GMa3(1+e2)(1−e2)A plantet is moving round the sun in an elliptical orbit as shows. As the planet moves from a to B
 Aits kinetic enargy will decreaseBits potential energy will remain unchangedCits angular momentum about centre of sun will remain unchangedDits speed is minimum at A
Aits kinetic enargy will decreaseBits potential energy will remain unchangedCits angular momentum about centre of sun will remain unchangedDits speed is minimum at A
A planet of mass m is in an elliptical orbit about the sun with an orbital period T. If A be the area of orbit, then its angular momentum would be
View SolutionTime taken by the particle to reach from A to B is t. Then the distance AB is equal to
View SolutionA planet revolves in an elliptical orbit around the sun. The semi-major and minor axes are a and b , then the time period is given by :
View SolutionIn the time taken by the projectile to reach from A to B is t. Then the distance AB is equal to.
 .
.
View Solution_S01_025_Q01.png)
The figure shows elliptical orbit of a planet m about the sun S. the shaded area SCD is twice the shaded area SAB. If t1 be the time for the planet to move from C to D and t2 is the time to move from A to B, then:
View Solution