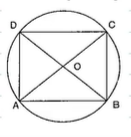
ACandBD are chords of a circle that bisect each other. Prove that: ACandBD are diameters ABCD is a rectangle.
We conclude from the given information
AB and CD are the two chords of a circle
Lets assume the point of intersection be O.
Construction
Join AB,BC,CD and AD.
In triangles AOB and COD,
∠AOB=∠COD ...(Vertically opposite angles)
OB=OD ....(O is the mid-point of BD)
OA=OC ....(O is the mid-point of AC)
△AOB≅△COD ....SAS test of congruence
∴AB=CD ....c.s.c.t.
Similarly,
we can prove
△AOD≅△BOC, then we get
AD=BC ....c.s.c.t.
So, □ABCD is a parallelogram, since opposite sides are equal in length.
So, opposite angles are equal as well.
So, ∠A=∠C
Also,
for a cyclic quadrilateral opposite angles add up to 180∘
So,
∠A+∠C=180∘
∠A+∠A=180∘
∠A=90∘
So,
BD is the diameter.
Similarly, AC is also the diameter.
(ii) Since AC and BD are diameters,
∴∠A=∠B=∠C=∠D=90∘ ...Angle inscribed in a semi circle is a right angle.
Hence, parallelogram ABCD is a rectangle..
Topper's Solved these Questions
Similar Questions
Knowledge Check
If AC and BD are two chords of a circle that bisect each other then quadrilateral ABCD is a
 ArectangleBsquareCtrapeziumDparallelogram
ArectangleBsquareCtrapeziumDparallelogram
AC and BD are chords of a circle which bisect each other. Prove that (i) AC and BD are diameters (ii) ABCD is a rectangle
View SolutionAC and BD are chords of a circle which bisect each other. Prove that (i) AC and BD arediameters, (ii) ABCD is a rectangle
View SolutionProve that the diagonals of a rectangle bisect each other and are equal.
View SolutionTwo segments AC and BD bisect each other at O . Prove that ABCD is a parallelogram.
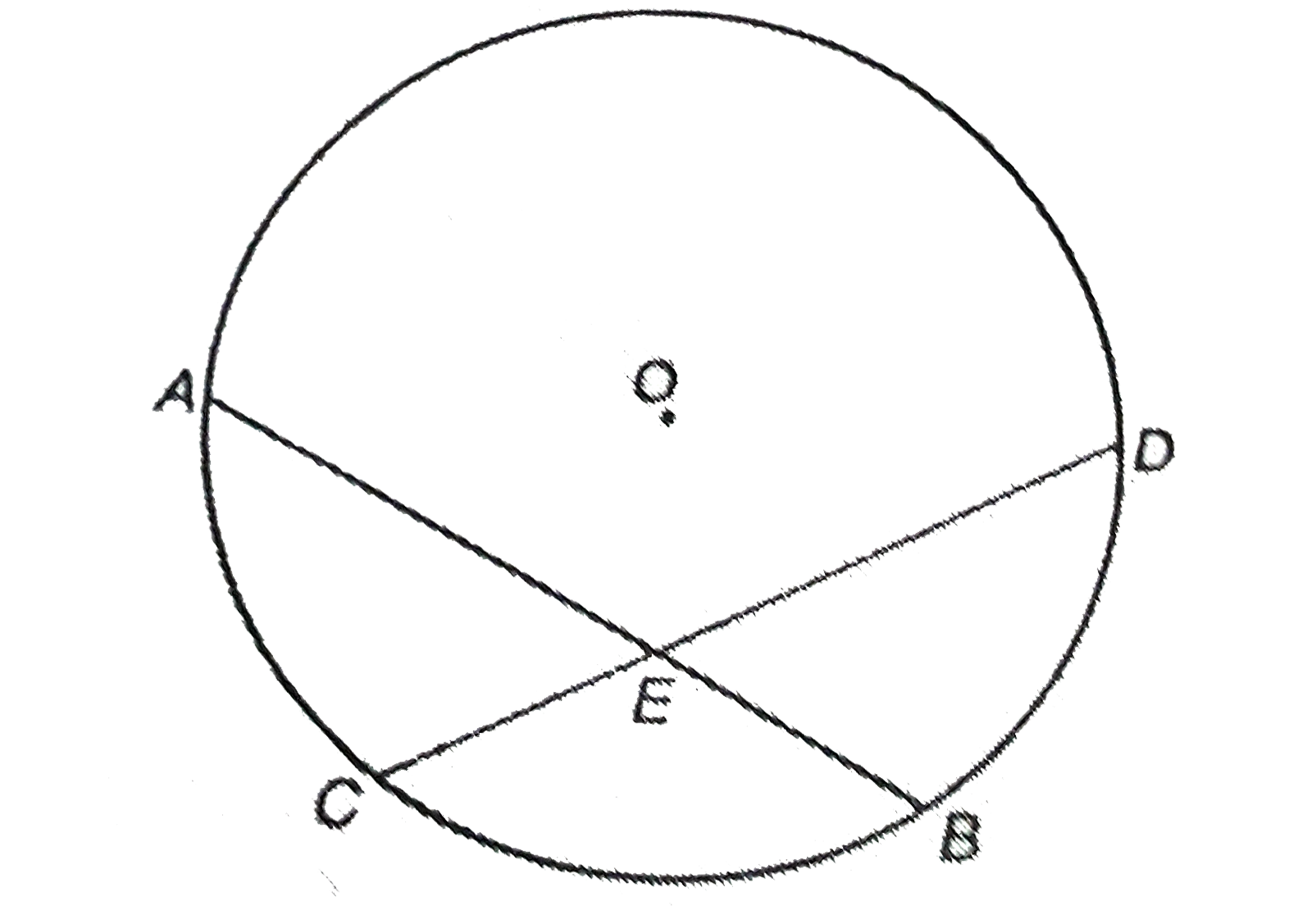
View SolutionIn the adjoining figure. If two equal chords AB and CD of a circle intersect each other at E. then prove that chords AC and DB are equal.
View SolutionIn figure, two circles intersect each other at points A and E. Their common secant through E intersects the circles at points B and D. The tangents of the circles at points B and D intersect each other at point C. Prove that □ ABCD is cyclic.

View SolutionIf a diameter of a circle bisects each of the two chords of a circle, prove that the chords are parallel.
View Solution