The bisector of ∠B of an isosceles triangle ABC with AB=AC meets the circumcircle of ABC at P as shown in Figure. If AP and BC produced meet at Q,. prove that CQ=CA
Since AB= AC, hence angle opposite to equal sides are also equal.
∠ACB=∠ABC.
Since, ext ∠ACB=∠QAC+∠AQC
Then, ∠ABC=∠QAC+∠AQC
Now, because ∠ABP=∠PBC.
Therefore,
2∠PBC=∠ABC
Hence,
2∠PBC=∠QAC+∠AQC
Now,
∠QAC=∠PAC and because APAC and APBC lie on same line segment PC.
So,
∠PAC=∠PBC
Hence
∠PBC=∠QAC
2∠PBC=∠PBC+AQC
∠PBC=∠AQC
∠PAC=∠AQC
∠QAC=∠AQC
Side opposite to equal sides are equal.
QC=AC
Hence prove.
Topper's Solved these Questions
Similar Questions
The bisector of ∠B of an isosceles triangle ABC with AB=AC meets the circumcircle of ABC at P as shown in Figure. If AP and BC produced meet at Q,. prove that CQ=CA
View SolutionThe bisector of ∠B of an isosceles triangle ABC with AB=AC meets the circumcircle of △ABC at P as shown in the figure. If AP and BC produced meet at Q prove that CQ=CA.
View Solution
Knowledge Check
In an isosceles triangle ΔABC,AB=AC and ∠A=80∘. The bisector of ∠Band∠C meet at D. The ∠BDC is equal to the
A90∘B100∘C130∘D80∘
Bisector AD of ∠BAC of ABC passes through the centre O of the circumcircle of ABC as shown in figure. Prove that AB=AC.
View SolutionABCD is a cyclic quadrilateral. ABandDC are produced to meet in E. Prove that EBC−EDA.
View SolutionIn a parallelogram ABCD, AB=10cm, AD=6cm. The bisector of ∠A meets DC in E, AE and BC produced meet at F. Find the length C Foot
View SolutionABCD is a quadrilateral. A line through D, parallel to AC, meets BC produced in P as shown in Figure. Prove that ar (ABP)=ar (Qua..ABCD).
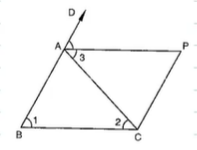
View SolutionIn Figure, ABC is an isosceles triangle in which AB=AC.CPparel≤lAB and AP is the bisector of exterior ∠CAD of ABC . Prove that ∠PAC=∠BCA and (ii) ABCP is a parallelogram.
View SolutionAn exterior angle of a triangle is 1100 , and one of the interior opposite angles is 300. Find the other two angles of the triangle.
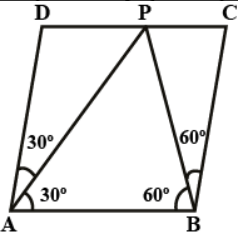
View SolutionIn Figure, ABCD is a parallelogram and ∠DAB=600. If the bisectors AP and BP of angles A and B respectively, meet at P on CD, prove that P is the mid-point of CD
View Solution

