AB is a diameter of a circle with centre O and radius OD is perpendicular to AB. If C is any point on arc DB, find ∠BAD and ∠ACD
Solution:
OA=OD
∠OAD=∠ADO(Angles opposite to equal sides are equal)
△AOD,
∠OAD+∠ADO+∠AOD=180∘
2OAD+90∘=180∘
∠OAD=902=45∘
∠AOD=2∠ACD
∠ACD=45∘
Hence the required answer is 45∘.
Topper's Solved these Questions
Similar Questions
AB is a diameter of a circle with centre O and radius OD is perpendicular to AB. If C is any point on arc DB, find ∠BAD and ∠ACD
View SolutionIn Fig. 10.36, A,B and C are three points on a circle with centre O such that ∠BOC= 30o and ∠AOB= 60o. If D is a point on the circle other than the arc ABC, find ∠ADC.
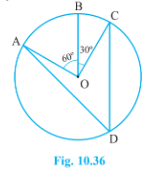
View Solution
Knowledge Check
Find the length of the tangent to a circle with centre O and radius 3 cm from a point P such that OP=5cm?
A7B4C8D1
In Fig. 71, if ABCD and CDEF, find ∠ACE
View SolutionIn Figure, AB is a diameter of the circle such that ∠A=350and ∠Q=250, find ∠PBR
View SolutionIf ABCD is a rhombus with ∠ABC=56∘, find the measure of ∠ACD
View SolutionIn Fig. 15.63, ABCD is a trapezium with ABDC and ∠BCD=60o . If BFEC is a sector of a circle with centre C and AB=BC=7 cm and DE=4 cm , then find the area of the shaded region (Use π=227 and √3=1.732) .
View SolutionIn Fig. 15.69, AB and CD are two diameters of a circle perpendicular to each other and OD is the diameter of the smaller circle. If OA=7 cm , find the area of the shaded region. (FIGURE)
View SolutionIn fig. 28.7 if the coordinates of point P are (a,b,c) then Write the coordinates of points A, B, C, D, E and F. Write the coordinates of the feet of the perpendiculars from the point P to the coordinate axes. Write the coordinates of the feet of the perpendicular from the point P on the coordinate planes XY, YZ and ZX. Find the perpendicular distances of point P from XY,YZ and ZX− planes. Find the perpendicular distances of the point P fro the coordinate axes. Find the coordinates of the reflection of P are (a,b,c) . Therefore OA=a, OB=b nd OC=⋅
View SolutionAB and CD are two parallel chords of a circle with centre O such that AB=6 cm and CD=12 cm. The chords are on the same side of the centre and the distance between them is 3 cm. The radius of the circle is 6 cm
View Solution
