AC and BD are chords of a circle which bisect each other. Prove that (i) AC and BD are diameters (ii) ABCD is a rectangle
We conclude from the given information that AB and CD are the two chords of a circle
Construction
Let the point of intersection be O.
Join AB,BC,CD and AD.
In triangles AOB and COD
,
∠AOB=∠COD ...(Vertically opposite angles)
OB=OD ....(O is the mid-point of BD)
OA=OC ....(O is the mid-point of AC)
△AOB≅△COD ....SAS test of congruence
∴AB=CD .... (by c.s.c.t.)
Similarly, we can prove
△AOD≅△BOC,
then we get
∴AD=BC ....(by c.s.c.t.)
So, □ABCD is a parallelogram, since opposite sides are equal in length.
So, opposite angles are equal as well.
So, ∠A=∠C
Also, for a cyclic quadrilateral opposite angles add up to 180∘So,
∠A+∠C=180∘
∠A+∠A=180∘
∠A=90∘
So, BD is the diameter. Similarly, AC is also the diameter.
Since AC and BD are diameters,
∴∠A=∠B=∠C=∠D=90∘ ...(Angle inscribed in a semi circle is a right angle)
Hence, parallelogram ABCD is a rectangle.
Topper's Solved these Questions
Similar Questions
AB and CD are two chords of a circle such that AB=6 cm, CD=12 cm and ABCD. If the distance between AB and CD is 3 cm, find the radius of the circle.
View SolutionIn figure AB=AC and CP∣∣BA and AP is the bisector of exterior ∠CAD of ABC . Prove that ∠PAC=∠BCA (ii) ABCP is a parallelogram
View SolutionIn Figure, AD and BE are medians of ABC and BE∣∣DF . Prove that CF=14AC
Consider △ABC Since AD is Median
⇒BD=BC⋯(1)
Since BE is Median⇒AE=EC⋯(2)
Consider △BECSince BE∣∣DF
By Basic Proportionality theorm, ⇒BDDC=EFFC
From (1)⇒CF=EF
⇒CF=12AE
From (2)⇒CF=14AC
View SolutionIf AB, BC and CD are equal chords of a circle with O as centre and AD diameter, then ∠AOB= 600 (b) 900 (c) 1200 (d) none of these
View SolutionDiagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar (AOD)=ar ( BOC). Prove that ABCD is a trapezium.
View SolutionIn Figure, ABCD is a parallelogram. E and F are the mid-points of the sides AB and CD respectively. Prove that the line segments AF and CE trisect (divide into three equal parts) the diagonal BD .
View SolutionABC and DBC are two isosceles triangles on the same bas BC and vertices A and D are on the same side of BC . If AD is extended to intersect BC at P, show that AP bisects \ ∠A as well as ∠D AP is the perpendicular bisector of BC
View SolutionABC and DBC are two isosceles triangles on the same bas BC and vertices A and D are on the same side of BC . If AD is extended to intersect BC at P, show that ABD ≅ACD (ii) ABP ≅ACP
View SolutionIn Figure, ABCD is a parallelogram and X and Y are points on the diagonal BD such that DX=BY . Prove that AXCY is a parallelogram (ii) AX=CY, AY=CX AYB ≅CXD (iv) AXD≅ CYB
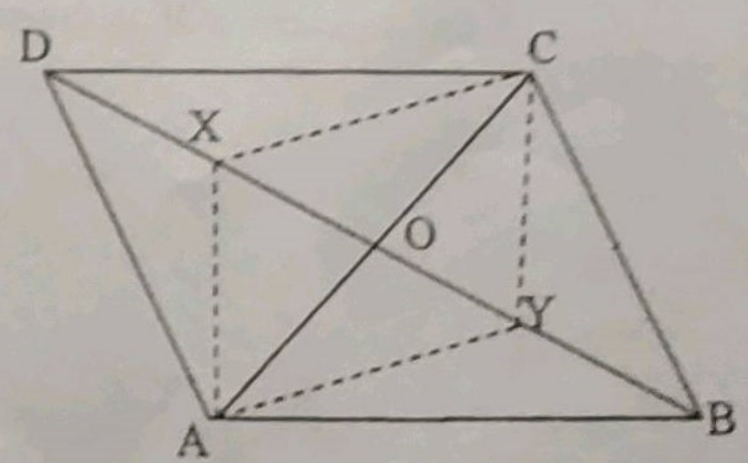
View SolutionA,B,CandD have position vectors →a,→b,→cand→d, respectively, such that →a−→b=2(→d−→c). Then a. ABandCD bisect each other b. BDandAC bisect each other c. ABandCD trisect each other d. BDandAC trisect each other
View Solution

