In any triangle ABC, if the angle bisector of ∠Aand perpendicular bisector of BCintersect, prove that they intersect on the circumcircle of the triangle ABC
Video Solution
Text Solution
Given: Angle bisector of angle A and perpendicular bisector of BC intersect.
Let the bisector of A meet the circumcircle at E.
In △ABE and △AEC,
∠BAE=∠CAE {AE Angle bisector of A}
∴BE=EC.....(1) {converse of the angle subtended by the chord of equal length at the same point are equal}
Let D be the midpoint of BC and now connect ED.
In △BDE and △CDE,
BE=CE ....from eq. (1)
BD=CD ...{D is mid point of BC}
DE=DE ...common side
∴△BDE≅△CDE ...SSS test of congruence
⇒∠BDE=∠CDE .....c.p.c.t.
Also,
∠BDE+∠CDE=180∘
...angles in linear pair
∴∠BDE=∠CDE=90∘
Therefore, DE is the right angled bisector of BC.
Hence, they intersect on the circumcircle of triangle ABC
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
In a triangle, with usual notations, the length of the bisector of angle A is
A2bcb+csinA2B2bcb+ccosA2Cabc2R(b+c)cosecA2D4Ab+ccosecA2In given triangle ABC ,AP is bisector of ∠BAC and AQ is perpendicular to BC then ∠PAQ is equal to
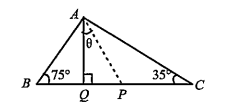 A20∘B40∘C15∘D25∘
A20∘B40∘C15∘D25∘The point of intersection of the angle bisectors of a triangle is :
AorthocentreBcentroidCincentreDcircumcentre
If in a triangle ABC,CD is the angular bisector of the angle ACB then CD is equal to
View SolutionProve that the internal bisectors of the angles of a triangle are concurrent
View SolutionIn a triangle ABC with ∠BCA=90∘, the perpendicular bisector of AB intersects segments AB and AC at X and Y, respectively. If the ratio of the area of quadrilateral BXYC be the area of triangle ABC is 13:18 and BC=12 then which is the length of AC?
View SolutionIn a triangle ABC, the bisector of angle A meets the opposite side at D. Using vectors prove that BD:DC=c:b.
View SolutionThe point of intersection of the angle bisectors of a triangle is :
View Solution

