In Figure, if ∠BAC=600 and ∠BCA=200, find ∠ADC
To solve the problem, we need to find the angle ∠ADC in the given cyclic quadrilateral ABCD where ∠BAC=60∘ and ∠BCA=20∘.
1. Identify the Angles in Triangle ABC:
- Given ∠BAC=60∘ and ∠BCA=20∘.
- Let ∠ABC=x.
2. Use the Triangle Sum Property:
- The sum of angles in triangle ABC is 180∘.
- Therefore, we can write the equation:
∠BAC+∠BCA+∠ABC=180∘
Substituting the known values:
60∘+20∘+x=180∘
- Simplifying this gives:
80∘+x=180∘
- Thus, x=180∘−80∘=100∘.
- Therefore, ∠ABC=100∘.
3. Identify the Cyclic Quadrilateral Property:
- In a cyclic quadrilateral, the opposite angles sum up to 180∘.
- Here, we have quadrilateral ABCD.
4. Apply the Cyclic Quadrilateral Property:
- We know ∠ABC+∠ADC=180∘.
- Substituting the value we found:
100∘+∠ADC=180∘
- Solving for ∠ADC:
∠ADC=180∘−100∘=80∘
Final Answer:
∠ADC=80∘
- Given ∠BAC=60∘ and ∠BCA=20∘.
- Let ∠ABC=x.
- The sum of angles in triangle ABC is 180∘.
- Therefore, we can write the equation:
∠BAC+∠BCA+∠ABC=180∘
Substituting the known values:
60∘+20∘+x=180∘
- Simplifying this gives:
80∘+x=180∘
- Thus, x=180∘−80∘=100∘.
- Therefore, ∠ABC=100∘.
- In a cyclic quadrilateral, the opposite angles sum up to 180∘.
- Here, we have quadrilateral ABCD.
- We know ∠ABC+∠ADC=180∘.
- Substituting the value we found:
100∘+∠ADC=180∘
- Solving for ∠ADC:
∠ADC=180∘−100∘=80∘
∠ADC=80∘
Topper's Solved these Questions
Similar Questions
ABCD is a cyclic quadrilateral in which: BCAD, ∠ADC=1100 and ∠BAC=500. Find ∠DAC ∠DBC=800 and ∠BAC=400. Find ∠BCD ∠BCD=1000and ∠ABD=700 find ∠ADB
View SolutionIn Figure, if EC∣∣AB, ∠ECD=700AND ∠BDO=200 , then ∠OBD is: 200 (b) 500 (c) 600 (d) 700
View SolutionThe diagonals of a parallelogram ABCD intersect at O . If ∠BOC=90∘ and ∠BDC=50∘, then ∠OAB= 40∘ (b) 50∘ (c) 10∘ (d) 900
View SolutionIn a parallelogram ABCD, the diagonals bisect each other at O. If ∠ABC=300, ∠BDC=100and ∠CAB=700, Find: ∠DAB, ∠ADC, ∠BCD, ∠AOD, ∠DOC, ∠BOC, ∠AOB, ∠ACD, ∠CAB, ∠ADB
Given that
∠ABC=302,∠ABC=∠ADC=300
[We know that measure of opposite angles are equal in a parallelogram]
∠BDC=100
∠CAB=700
∠BDA=∠ADB=∠ADC–∠BDC
302–102=202
∠DAB=1800–300=1500
∠ADB=∠DBC=200 (alternate angles)
∠BCD=∠DAB=1500
[we know, opposite angles are equal in a parallelogram]
∠DBA=∠BDC=100
[we know, Alternate interior angles are equal]
InΔABC
∠CAB+∠ABC+∠BCA=1800
[since, sum of all angles of a triangle is 180^0]
700+300+∠BCA=1800
∠BCA=1800–1000=800
∠DAB=∠DAC+∠CAB=700+800=1500
∠BCD=1500 (opposite angle of the parallelogram)
∠DCA=∠CAB=700
In ΔDOC∠BDC+∠ACD+∠DOC=1800
[since, sum of all angles of a triangle is 180^0]
100+700+∠DOC=1800
∠DOC=1800−800
∠ACB=800
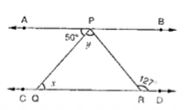
View SolutionIn Figure, if AB∣∣CD, ∠APQ=500AND ∠PRD=1270, find x and y
View SolutionIn a parallelogram ABCD , if ∠DAB=75∘and ∠DBC=60∘, then ∠BDC=(a) 75∘ (b) 60∘ (c) 45∘ (d) 55∘
View SolutionD is a point on the side BC of ABC. A line PDQ , though D , meets side AC in P and AB produced at Q . If ∠A=800, ∠ABC=600 and ∠PDC=150 find (i) ∠AQD (ii) ∠APD.
View SolutionIn Figure, PQ∣∣RS, ∠AEF=950, ∠BHS=1100 and ∠ABC=x0. Then the value of x is (a)150 (b) 250 (c) 700 (d) 350
View SolutionThe side BC of ABC is produced to a point D. The bisector of ∠A meets side BC in L. If ∠ABC=300and ∠ACD=1150, then ∠ALC= 850 (b) 72120 (c) 1450 (d) none of these
View SolutionIn Fig. 71, if ABCD and CDEF, find ∠ACE
View Solution

