ABCD is a cyclic quadrilateral in which: BCAD, ∠ADC=1100 and ∠BAC=500. Find ∠DAC ∠DBC=800 and ∠BAC=400. Find ∠BCD ∠BCD=1000and ∠ABD=700 find ∠ADB
ABCD is a cyclic quadrilateral
AD∣∣BC,∠ADC=1100
∠BAC=500
∠B+∠D=1800(Sum of opposite angles)
∠B+1100=1800
∠B=1800−1100
∠B=700
Now in △ABC,∠CAB+∠ABC+∠BCA=1800
500+700+∠BCA=1800
∠BAC=1800−1200=600
But ∠DAC=∠BCA( alternate angles)
∠DAC=600
ii) arcDC subtends ∠DBCand ∠DAC in the same segment
∠DBC=∠DAC=800
∠DBC=∠DAC+∠CAB=800+400=1200
∠DAB+∠BCD=1800(Sum of opposite angles of a cyclic quadrilateral).
1200+∠BCD=1800
∠BCD=1800−1200=600
iii) ABCD is cyclic quadrilateral and BD is joined.
∠BCD=1000and ∠ABD=700
∠A+∠C=1800(Sum of opposite angles of cyclic quadrilateral)
∠A+1000=1800
∠A=1800−100=800
Now in △ABD,∠A+∠ABD+∠ADB=1800
800+700+∠ADB=1800
∠ADB=1800−1500
∠ADB=300
Topper's Solved these Questions
Similar Questions
Knowledge Check
If ABCD is a cyclic quadrilateral with ∠A=50∘,∠B=80∘, then Cand∠D are
A100∘,130∘B115∘,115∘C110∘,120∘D130∘,100∘
In Fig.84, ABCD and AECF; ∠FCG=900 and ∠BAC=1200. Find the values of x,y and z.
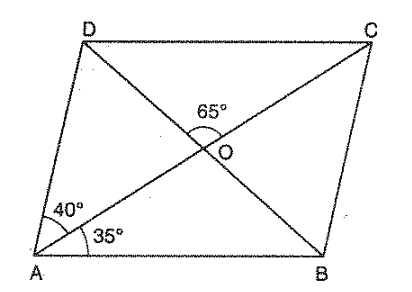
View SolutionIn Figure, ABCD is a parallelogram in which ∠DAO=400, ∠BAO=350 and ∠COD=650. Find: ∠ABO (ii) ∠ODC (iii) ∠ACB (iv) ∠CBD
View SolutionIn a parallelogram ABCD, the diagonals bisect each other at O. If ∠ABC=300, ∠BDC=100and ∠CAB=700, Find: ∠DAB, ∠ADC, ∠BCD, ∠AOD, ∠DOC, ∠BOC, ∠AOB, ∠ACD, ∠CAB, ∠ADB
Given that
∠ABC=302,∠ABC=∠ADC=300
[We know that measure of opposite angles are equal in a parallelogram]
∠BDC=100
∠CAB=700
∠BDA=∠ADB=∠ADC–∠BDC
302–102=202
∠DAB=1800–300=1500
∠ADB=∠DBC=200 (alternate angles)
∠BCD=∠DAB=1500
[we know, opposite angles are equal in a parallelogram]
∠DBA=∠BDC=100
[we know, Alternate interior angles are equal]
InΔABC
∠CAB+∠ABC+∠BCA=1800
[since, sum of all angles of a triangle is 180^0]
700+300+∠BCA=1800
∠BCA=1800–1000=800
∠DAB=∠DAC+∠CAB=700+800=1500
∠BCD=1500 (opposite angle of the parallelogram)
∠DCA=∠CAB=700
In ΔDOC∠BDC+∠ACD+∠DOC=1800
[since, sum of all angles of a triangle is 180^0]
100+700+∠DOC=1800
∠DOC=1800−800
∠ACB=800
View SolutionIn a quadrilateral ABCD, ∠A+∠C is 2 times ∠B+∠D. If ∠A=140∘ and ∠D=60∘, then ∠B= 60∘ (b) 80∘ (c) 120∘ (d) None of these
View SolutionABCD is a parallelogram in which diagonal AC bisects ∠BAD. If ∠BAC=35∘ , then ∠ABC= 70∘ (b) 110∘ (c) 90∘ (d) 120∘
View SolutionIn Fig.80, line ACl∈e DE and ∠ABD=320. Find out the angles x and y if ∠E=1220.
View SolutionThe diagonals of a parallelogram ABCD intersect at O . If ∠BOC=90∘ and ∠BDC=50∘, then ∠OAB= 40∘ (b) 50∘ (c) 10∘ (d) 900
View Solution

