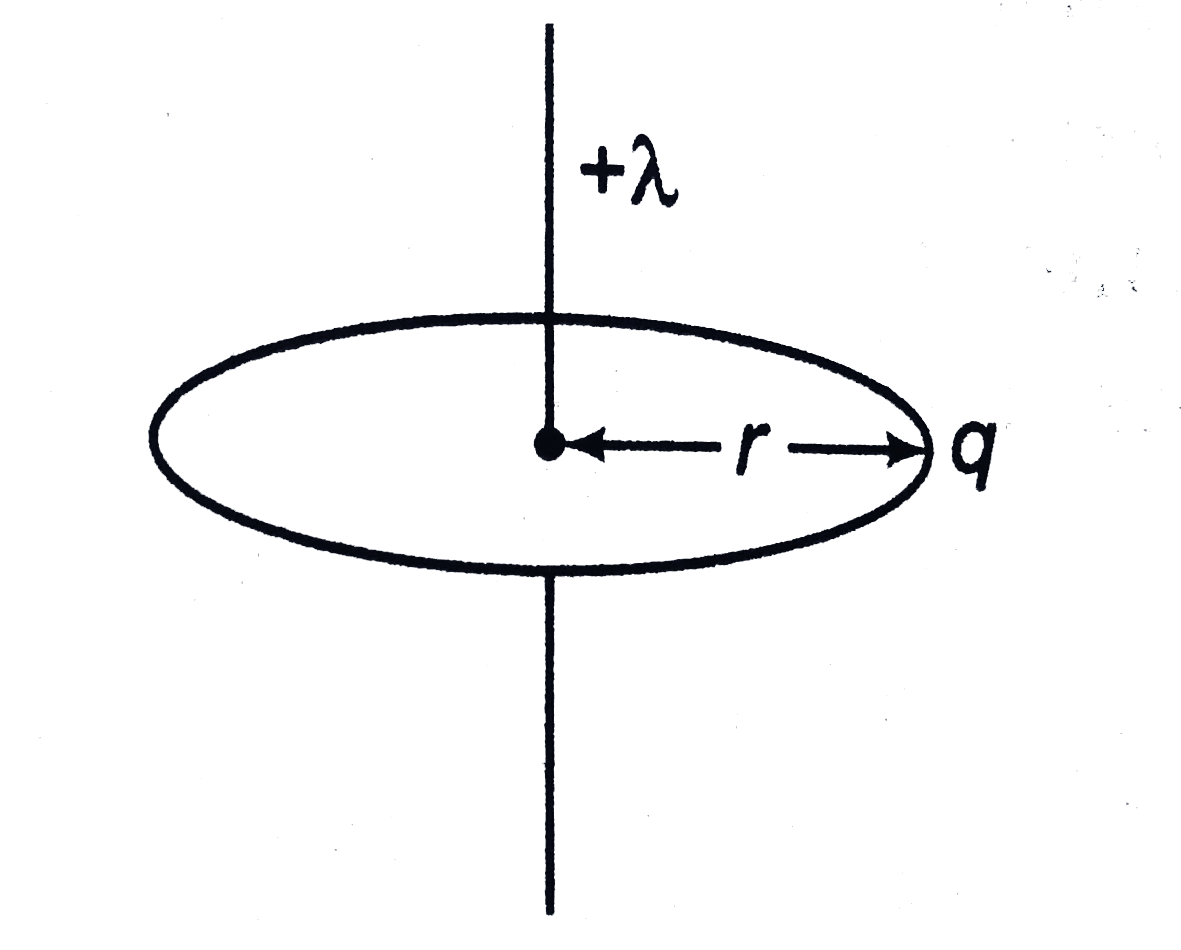
A particle of charge −q and mass m moves in a circle of radius r around an infinitely long line charge of linear charge density +λ. Then, time period will be
 where , k=14πε0)
where , k=14πε0)
T=2πr√m2kλq
T2=4π2m2kλqr3
T2=12πr√2kλqm
T=12πr√m2kλq where k=14πε0
The correct Answer is:A
We have centripetal force equation
q(2kλr)=mv2rsov=√2kqλmNow,
T=2πrv=√m2kλq where k=14πε0
Topper's Solved these Questions
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:Passage I
Explore 3 Videos
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:Passage II
Explore 3 Videos
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:NCERT based Question
Explore 14 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:NARAYNAChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:ADDITIONAL PROBLEMS
Explore 14 Videos
- EXPERIMENTAL PHYSICSBook:NARAYNAChapter:EXPERIMENTAL PHYSICSExercise:Comprehension type
Explore 6 Videos
Similar Questions
Knowledge Check
A particle of charge −q and mass m moves in a circular orbits of radius r about a fixed charge +Q.The relation between the radius of the orbit r and the time period T is
Ar=Qq16π2ε0MT3Br3=Qq16π2ε0MT2Cr2=Qq16π3ε0mT3Dr2=Qq16π3ε0mT3A charge moves with a speed v in a circular path of radius r around a long uniformly charged conductor.
Av∝rBv∝1rCv∝1√rDv∝r0Find ratio of electric at point A and B. Infinitely long uniformly charged wire with linear charge density λ is kept along z-axis:
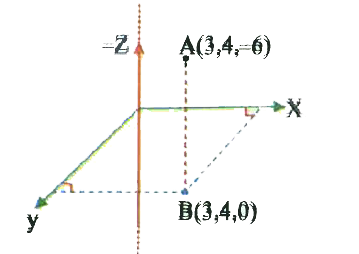 A1:2B1:6C6:1D1:1
A1:2B1:6C6:1D1:1
A particle of charge q1 and mass m is revolving around a fixed negative charge of magnitude q2 in a circular path of radius r. Find the time period of revolution.
View SolutionA charged particle q of mass m is in wquilibrium at a height h from a horizontal infinite line charge wit uniform linear charge density λ. The charge lies in the vertical plane containing the line charge. If the particle is displaced slightly (vertically) prove that the motion of the charged particle will be simple harmonic. Also find its time period.
View SolutionOn rotating a point charge g around a charge Q in a circle of radius r, the work done is
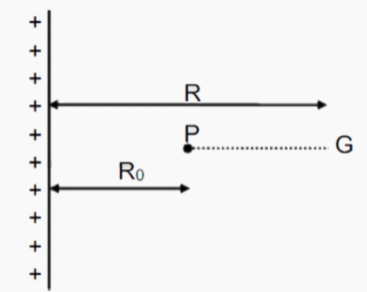
View SolutionA charge particle q is released at a distance R∘ from the infinite long wire of linear charge density λ. Then velocity will be proportional to (At distance R from the wire)
View SolutionA charge particle (charge q ) is moving in a circle of radius R with uniform speed. v The associated magnetic moment m is given by
View Solution

