In space of horizontal EF(E=(mg)/q) exist as shown in figure and a mass m is released at the end of a light rod. If mass m is releases from the position shown in figure find the angular velocity of the rod when it passes through the bottom most position
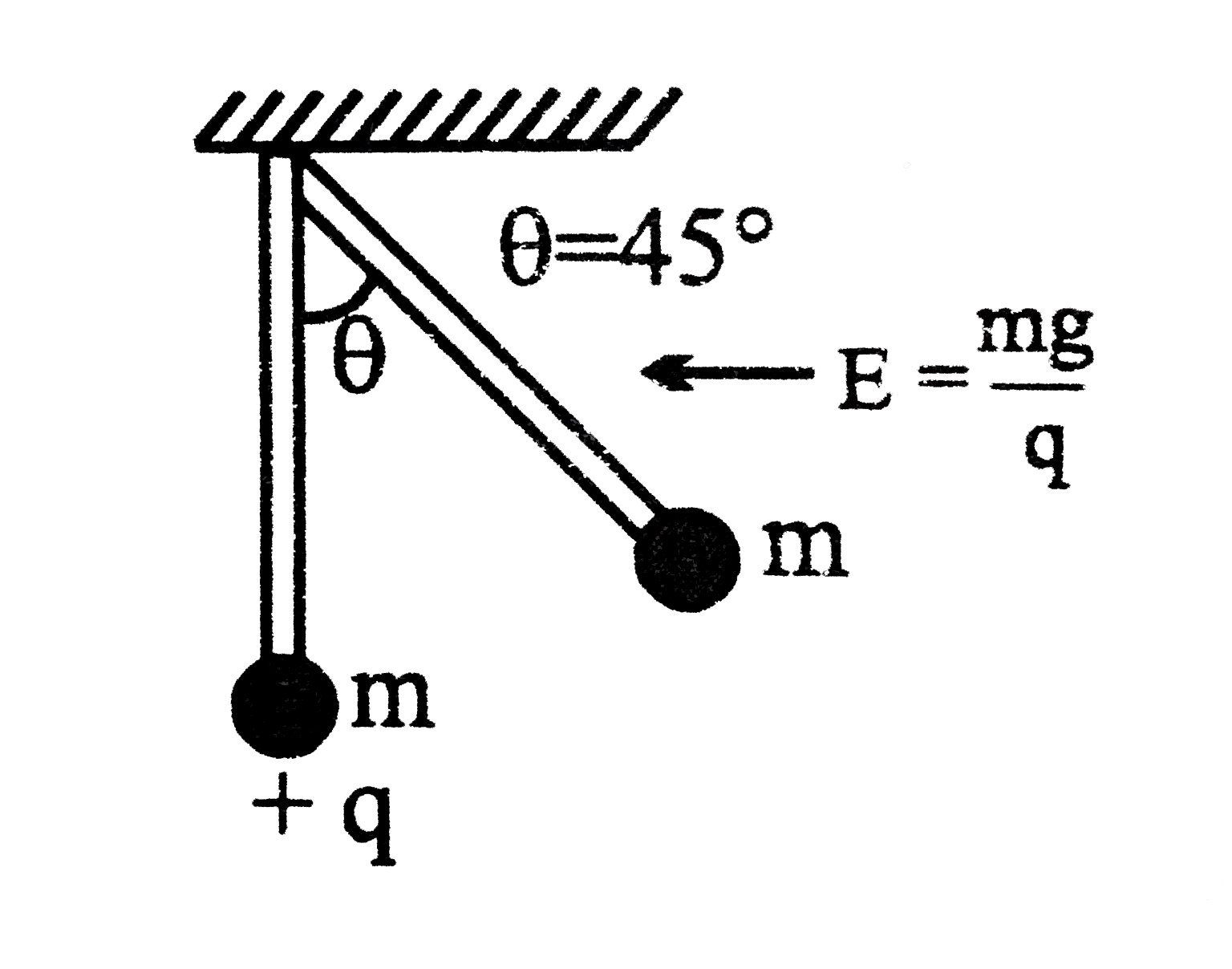 .
.
√gl
√2gl
√3gl
√5gl
The correct Answer is:B
WE+Wg=ΔK.E
Use work energy theorem
(Eq)lsinθ+mgl(1−cosθ)=12IωQ2
Topper's Solved these Questions
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:Passage I
Explore 3 Videos
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:Passage II
Explore 3 Videos
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:NCERT based Question
Explore 14 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:NARAYNAChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:ADDITIONAL PROBLEMS
Explore 14 Videos
- EXPERIMENTAL PHYSICSBook:NARAYNAChapter:EXPERIMENTAL PHYSICSExercise:Comprehension type
Explore 6 Videos
Similar Questions
A rod is released from the horizontal position as shown. It is free to rotate about hinge. Find angular velocity of rod when it become vertical?
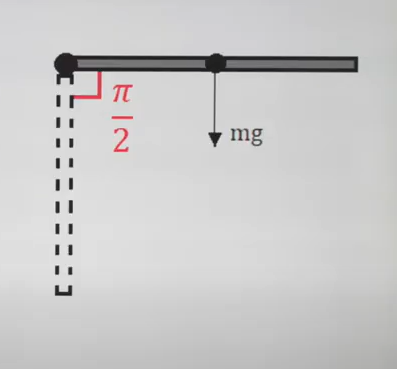
View Solution
A uniform disc of mass M and radius R is pivoted about the horizontal axis through its centre C A point mass m is glued to the disc at its rim, as shown in figure. If the system is released from rest, find the angular velocity of the disc when m reaches the bottom point B.
View Solution
Knowledge Check
If the masses are released from the position shown in figure then the speed of mass m1 just before it strikes the floor is -
 A[2m1gd/(m1+m2)]1/2B[2(m1−m2)gd/(m1+m2)]1/2C[2(m1−m2)gd/m1]1/2DNone of the above
A[2m1gd/(m1+m2)]1/2B[2(m1−m2)gd/(m1+m2)]1/2C[2(m1−m2)gd/m1]1/2DNone of the aboveA uniform thin rod of length l and mass m is hinged at a distance l/4 from one of the end and released from horizontal position as shown in Fig. The angular velocity of the rod as it passes the vertical position is
 A2√5g7lB2√6g7lC√3g7lD2√gl
A2√5g7lB2√6g7lC√3g7lD2√glIn the above problem, if the rod is released from horizontal position, the angular velocity of the rod as it passes the vertical position is (l=length fo rod)
A√12g5lB√2g3lC√3glD√3g7l
A block of mass m is released from a wedge of mass m as shown in figure . Find the time taken by the block to reach the end of the wedge.
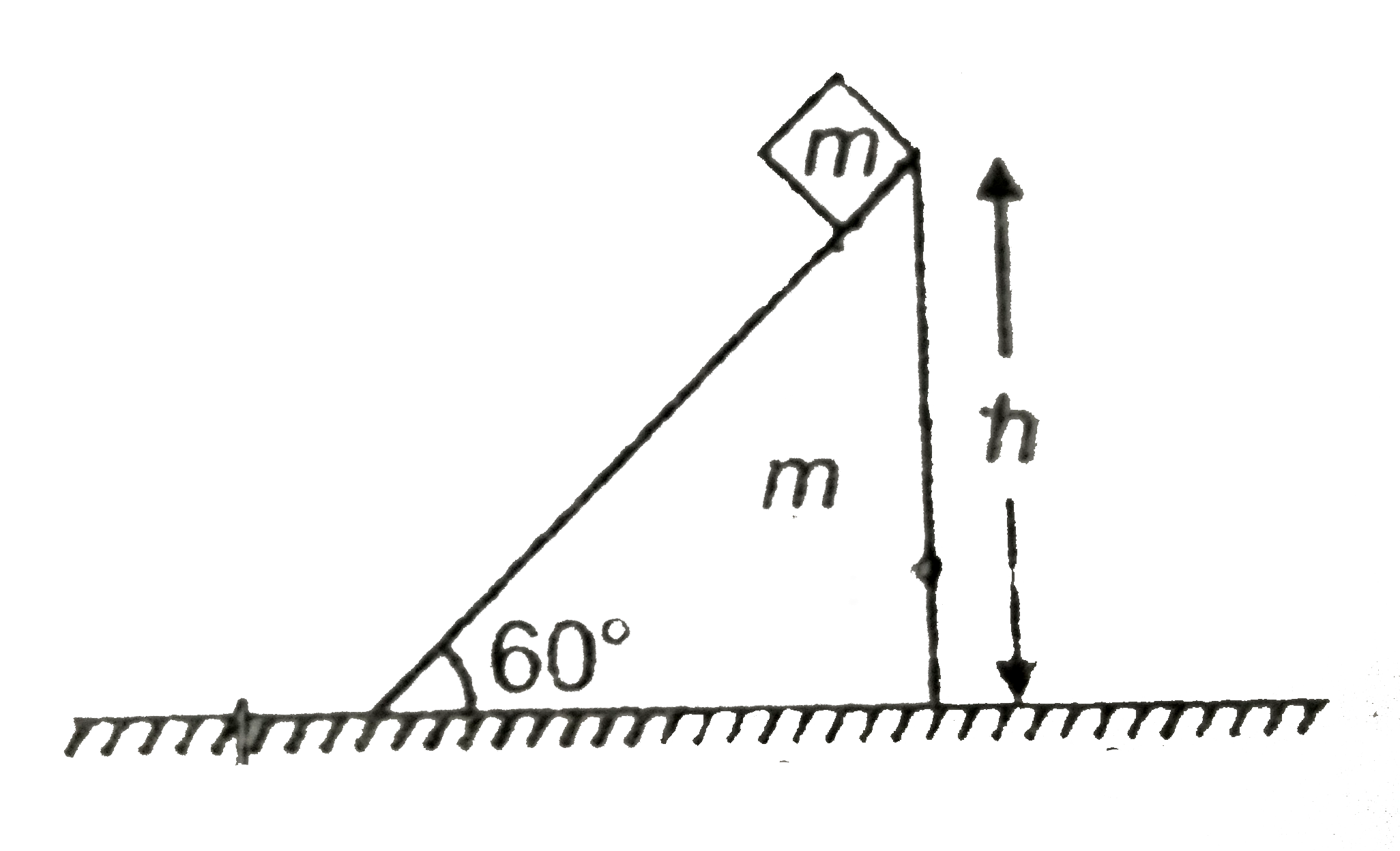
View SolutionA rod of length L is hinged from one end. It is brought to horizontal position and released. The angular velocity of the rod when it is in vertical position. Is
View SolutionA uniform thin rod of length l and mass m is hinged at a distance l/4 from one of the end and released from horizontal position as shown in Fig. The angular velocity of the rod as it passes the vertical position is

View SolutionA L shaped rod of mass M is free to rotate in a vertical plane about axis A A as shown in figure. Maximum angular acceleration of rod is

View SolutionA rod of length L is hinged from one end. It is brought to a horizontal position and released. The angular velocity of the rod, when it is in vertical position, is
View Solution

