a point charge q is placed at the centre of a cylinder of length L and radius R the electric flux through the curved surface of the cylinder is
qε0L√L2+R2
qε0L√L2+2R2
qε0L√L2+4R2
q2ε0
The correct Answer is:C
To find the electric flux through the curved surface of a cylinder with a point charge q placed at its center, we can follow these steps:
Step 1: Understand the Geometry
We have a cylinder of length L and radius R with a point charge q at its center. The cylinder has two circular flat surfaces and one curved surface.
Step 2: Apply Gauss's Law
According to Gauss's Law, the total electric flux Φ through a closed surface is given by:
Φ=qencϵ0
where qenc is the charge enclosed by the surface, and ϵ0 is the permittivity of free space. Since the charge q is at the center of the cylinder, the total electric flux through the entire closed surface of the cylinder is:
Φtotal=qϵ0
Step 3: Calculate Flux through Flat Surfaces
The flux through the two flat circular surfaces (let's call them Φ1 and Φ2) will be equal due to symmetry. Let Φf be the flux through one flat surface. Therefore, the total flux through both flat surfaces is:
Φflat=2Φf
Step 4: Relate Total Flux to Curved Surface Flux
The total flux through the cylinder can be expressed as the sum of the flux through the curved surface Φc and the flux through the flat surfaces:
Φtotal=Φc+Φflat
Substituting the expressions we have:
qϵ0=Φc+2Φf
Step 5: Calculate Flux through Flat Surface
To find Φf, we can use the fact that the electric field due to the charge q at the center of the cylinder is uniform over the flat surfaces. The electric field E at the surface of the flat circular face can be calculated using:
E=q2πR2ϵ0
The area A of one flat surface is:
A=πR2
Thus, the flux through one flat surface is:
Φf=E⋅A=(q2πR2ϵ0)⋅(πR2)=q2ϵ0
Step 6: Substitute Back to Find Curved Surface Flux
Now substituting Φf back into the equation for total flux:
qϵ0=Φc+2(q2ϵ0)
This simplifies to:
qϵ0=Φc+qϵ0
Thus, we find:
Φc=qϵ0−qϵ0=0
Step 7: Calculate the Curved Surface Flux
However, we need to consider the geometry of the cylinder more carefully. The flux through the curved surface can be derived from the total flux minus the flux through the flat surfaces.
Using the geometry of the cylinder, we can derive that:
Φc=qϵ0−2(q2ϵ0)=qϵ0−qϵ0=0
Final Result
Thus, the electric flux through the curved surface of the cylinder is given by:
Φc=qϵ0⋅L√L2+4R2
We have a cylinder of length L and radius R with a point charge q at its center. The cylinder has two circular flat surfaces and one curved surface.
According to Gauss's Law, the total electric flux Φ through a closed surface is given by:
Φ=qencϵ0
where qenc is the charge enclosed by the surface, and ϵ0 is the permittivity of free space. Since the charge q is at the center of the cylinder, the total electric flux through the entire closed surface of the cylinder is:
Φtotal=qϵ0
The flux through the two flat circular surfaces (let's call them Φ1 and Φ2) will be equal due to symmetry. Let Φf be the flux through one flat surface. Therefore, the total flux through both flat surfaces is:
Φflat=2Φf
The total flux through the cylinder can be expressed as the sum of the flux through the curved surface Φc and the flux through the flat surfaces:
Φtotal=Φc+Φflat
Substituting the expressions we have:
qϵ0=Φc+2Φf
To find Φf, we can use the fact that the electric field due to the charge q at the center of the cylinder is uniform over the flat surfaces. The electric field E at the surface of the flat circular face can be calculated using:
E=q2πR2ϵ0
The area A of one flat surface is:
A=πR2
Thus, the flux through one flat surface is:
Φf=E⋅A=(q2πR2ϵ0)⋅(πR2)=q2ϵ0
Now substituting Φf back into the equation for total flux:
qϵ0=Φc+2(q2ϵ0)
This simplifies to:
qϵ0=Φc+qϵ0
Thus, we find:
Φc=qϵ0−qϵ0=0
However, we need to consider the geometry of the cylinder more carefully. The flux through the curved surface can be derived from the total flux minus the flux through the flat surfaces.
Φc=qϵ0−2(q2ϵ0)=qϵ0−qϵ0=0
Thus, the electric flux through the curved surface of the cylinder is given by:
Φc=qϵ0⋅L√L2+4R2
Topper's Solved these Questions
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:Passage I
Explore 3 Videos
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:Passage II
Explore 3 Videos
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:NCERT based Question
Explore 14 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:NARAYNAChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:ADDITIONAL PROBLEMS
Explore 14 Videos
- EXPERIMENTAL PHYSICSBook:NARAYNAChapter:EXPERIMENTAL PHYSICSExercise:Comprehension type
Explore 6 Videos
Similar Questions
Knowledge Check
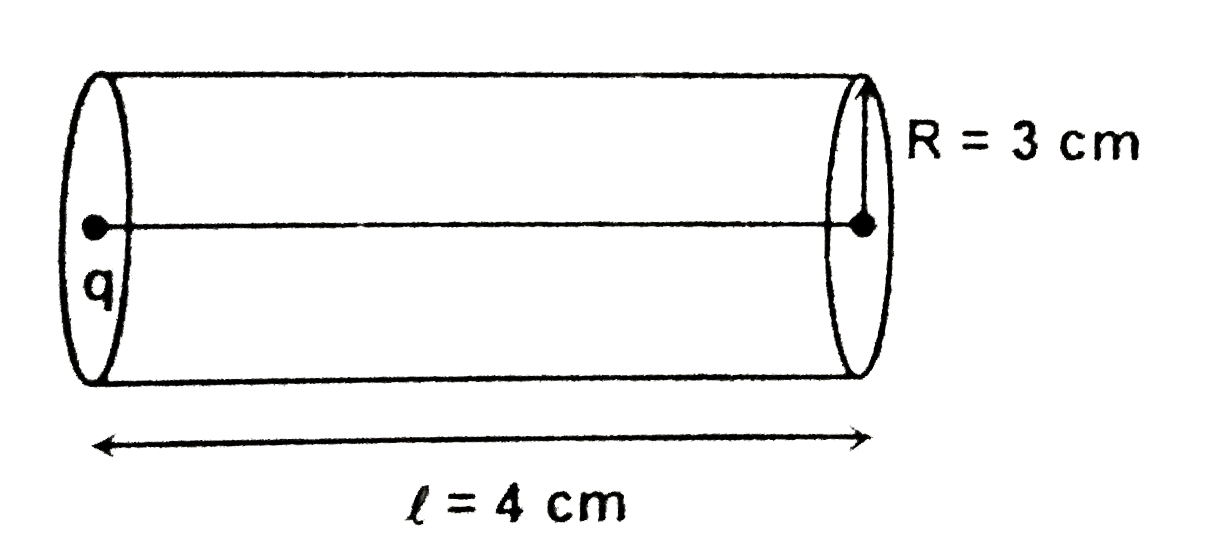
A point charge 'q' is placed at the centre of left circular end of a cylinder of length l=4cm and radius R=3 cm shown. Then the electric flux through the curved surface of the cylinder isAq5ε0B2q5ε0C3q5ε0D4q5ε0An infinite line charge is at the axis of a cylinder of length 1 m and radius 7 cm. If electric field at any point on the curved surface of cylinder is 250 NC−1, then net electric flux through the cylinder is
A1.1×102 Nm2C−1B9.74×10−6 Nm2C−1C5.5×106 Nm2C−1D2.5×102 Nm2C−1A charge q is placed at the centre of the open end of a cylindrical vessel . The flux of the electric field through the surface of the vessel is
 AzeroBqε0Cq2ε0D2q2ε0.
AzeroBqε0Cq2ε0D2q2ε0.
A charge of 8.85C is placed at the centre of a spherical Gaussian surface of radius 5cm .The electric flux through the surface ..
View SolutionA point charge Q is placed at the centre of a hemisphere. Find the ratio of electric flux passing through curved andplane surface of the hemisphere.
View SolutionA point charge q is placed at the centre of a cube of side length a .The electric flux emerging from one of the face of cube is
View SolutionA point charge Q is placed at the centre of a hemisphere. Find the electric flux passing through flat surface of hemisphere.
View SolutionA charge Q is placed at the centre of a cub. Find the flux of the electric field through the six surfaced of the cube.
View Solution

