N fundamental charges each of charge q are to be distributed as two point charges separated by a fixed distance ,then the maximum to minimum force bears a ratio (N is even and greater than 2)
(N−1)24N2
4N2(N−1)
N24(N−1)
2N2(N−1)
The correct Answer is:3
To solve the problem, we need to find the ratio of the maximum to minimum force between two point charges formed by distributing N fundamental charges, each of charge q, separated by a fixed distance r.
1. Understanding the Charges Distribution:
- We have N fundamental charges, each of charge q.
- We can distribute these charges into two groups: one group with n charges and the other with N−n charges.
2. Calculating the Force Between the Charges:
- The force between two point charges is given by Coulomb's Law:
\(
F = k \frac{q_1 q_2}{r^2}
\)
- Here, \( q_1 = n \cdot q \) and \( q_2 = (N - n) \cdot q \).
- Substituting these into the formula gives:
\(
F = k \frac{(n \cdot q)((N - n) \cdot q)}{r^2} = k \frac{n(N - n)q^2}{r^2}
\)
3. Finding Maximum and Minimum Forces:
- The expression for force can be rewritten as:
\(
F = k \frac{q^2}{r^2} \cdot n(N - n)
\)
- To maximize and minimize \( n(N - n) \), we recognize that this is a quadratic function in terms of \( n \).
4. Using AM-GM Inequality:
- The maximum value of \( n(N - n) \) occurs when \( n = \frac{N}{2} \) (since \( N \) is even).
- At this point:
\(
F_{\text{max}} = k \frac{q^2}{r^2} \cdot \left(\frac{N}{2}\right)\left(N - \frac{N}{2}\right) = k \frac{q^2}{r^2} \cdot \frac{N^2}{4}
\)
5. Finding the Minimum Force:
- The minimum value occurs when \( n = 1 \):
\(
F_{\text{min}} = k \frac{q^2}{r^2} \cdot 1(N - 1) = k \frac{q^2}{r^2} \cdot (N - 1)
\)
6. Calculating the Ratio of Maximum to Minimum Force:
- Now we find the ratio:
\(
\text{Ratio} = \frac{F_{\text{max}}}{F_{\text{min}}} = \frac{k \frac{q^2}{r^2} \cdot \frac{N^2}{4}}{k \frac{q^2}{r^2} \cdot (N - 1)} = \frac{\frac{N^2}{4}}{N - 1}
\)
- Simplifying this gives:
\(
\text{Ratio} = \frac{N^2}{4(N - 1)}
\)
Final Answer:
The ratio of the maximum to minimum force is:
\(
\frac{N^2}{4(N - 1)}
\)
- We have N fundamental charges, each of charge q.
- We can distribute these charges into two groups: one group with n charges and the other with N−n charges.
- The force between two point charges is given by Coulomb's Law:
\(
F = k \frac{q_1 q_2}{r^2}
\)
- Here, \( q_1 = n \cdot q \) and \( q_2 = (N - n) \cdot q \).
- Substituting these into the formula gives:
\(
F = k \frac{(n \cdot q)((N - n) \cdot q)}{r^2} = k \frac{n(N - n)q^2}{r^2}
\)
- The expression for force can be rewritten as:
\(
F = k \frac{q^2}{r^2} \cdot n(N - n)
\)
- To maximize and minimize \( n(N - n) \), we recognize that this is a quadratic function in terms of \( n \).
- The maximum value of \( n(N - n) \) occurs when \( n = \frac{N}{2} \) (since \( N \) is even).
- At this point:
\(
F_{\text{max}} = k \frac{q^2}{r^2} \cdot \left(\frac{N}{2}\right)\left(N - \frac{N}{2}\right) = k \frac{q^2}{r^2} \cdot \frac{N^2}{4}
\)
- The minimum value occurs when \( n = 1 \):
\(
F_{\text{min}} = k \frac{q^2}{r^2} \cdot 1(N - 1) = k \frac{q^2}{r^2} \cdot (N - 1)
\)
- Now we find the ratio:
\(
\text{Ratio} = \frac{F_{\text{max}}}{F_{\text{min}}} = \frac{k \frac{q^2}{r^2} \cdot \frac{N^2}{4}}{k \frac{q^2}{r^2} \cdot (N - 1)} = \frac{\frac{N^2}{4}}{N - 1}
\)
- Simplifying this gives:
\(
\text{Ratio} = \frac{N^2}{4(N - 1)}
\)
The ratio of the maximum to minimum force is:
\(
\frac{N^2}{4(N - 1)}
\)
Topper's Solved these Questions
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:Level III (C.W)
Explore 55 Videos
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:Level 1
Explore 8 Videos
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:Level 1(C.W)
Explore 24 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:NARAYNAChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:ADDITIONAL PROBLEMS
Explore 14 Videos
- EXPERIMENTAL PHYSICSBook:NARAYNAChapter:EXPERIMENTAL PHYSICSExercise:Comprehension type
Explore 6 Videos
Similar Questions
Knowledge Check
Two point charges Q and −Q/4 are separated by a distance X. Then
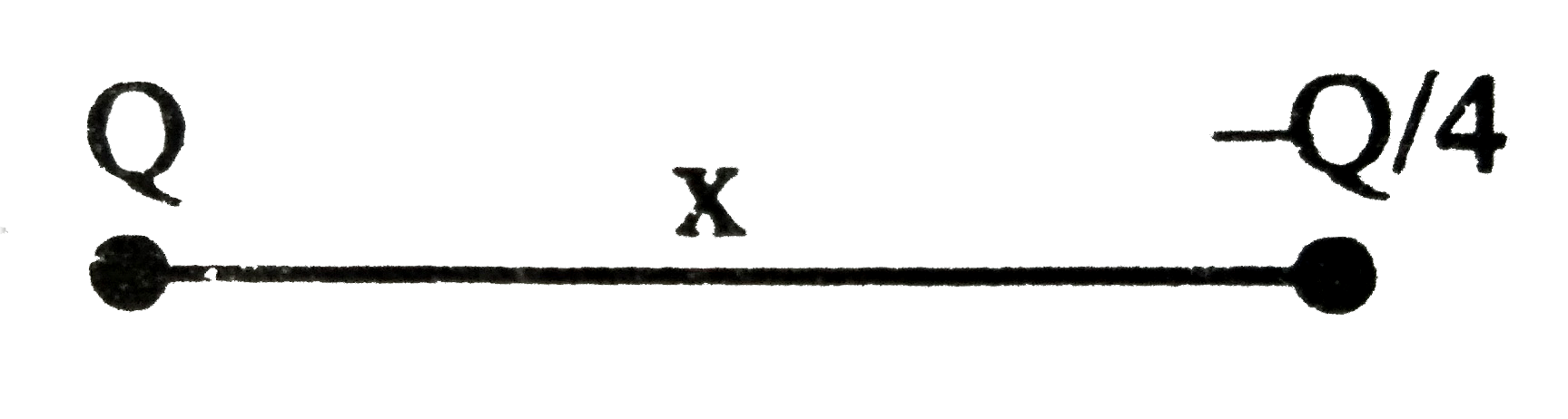 .Apotential is zero at a point on the axis which is x/3 on the right side of the cahrge −q/4Bpotential is zero at a point on the axis which is x/5 on the left side fo the charge −Q/4Celectric field is zero at a point on the axis which is at a distance x on the right side fo the charge −Q/4Dthere exist two points on the axis where electric field is zero.
.Apotential is zero at a point on the axis which is x/3 on the right side of the cahrge −q/4Bpotential is zero at a point on the axis which is x/5 on the left side fo the charge −Q/4Celectric field is zero at a point on the axis which is at a distance x on the right side fo the charge −Q/4Dthere exist two points on the axis where electric field is zero.Magnitude of force between two point charges q1 and q2 which are separated by a distance r is given by
AF=k|q1q2|rBF=k|q1q2|rr2CF=k(|q1q2|r)2DF=k|q1q2|r2Each of the two point charges are doubled and their distance is halved. Force of interaction becomes n times where n is
A5B1C0.16666666666667D16
Find out potential energy of the two point charge system having charges q1 and q2 separated by distance r.
View SolutionTwo point charge separeted by a distance d repel each other with a force of 9 N. If the separat becomes 3d, the force of repulsion will be
View SolutionF is the force and r is the distance between two charges q. If charges are halved and distance is doubled, then the new force will
View SolutionThere are two charges +1 μC and +5μC, separated by a distance of 0.2 m in air, the ratio of forces acting in them will be:
View SolutionA charge Q exerts a 12 N force on another charge q. If the distance between the charges is doubled, what is the magnitude of the force exerted on Q by q?
View Solution

