Find out potential energy of the two point charge system having charges $q_{1}$ and $q_{2}$ separated by distance r.

Video Solution

Text Solution

Generated By DoubtnutGPT

To find the potential energy of a two-point charge system with charges $q_{1}$ and $q_{2}$ separated by a distance $r$ , we can follow these steps:
1. Understanding the System:
We have two point charges, $q_{1}$ and $q_{2}$ , separated by a distance $r$ . The potential energy of this system is related to the work done in bringing these charges from infinity to their positions.
2. Work Done on Charge $q_{1}$ :
When charge $q_{1}$ is brought from infinity to a point in space where charge $q_{2}$ is already present, we need to calculate the work done, $W_{1}$ . Since $q_{2}$ is present, the potential $V$ at the location of $q_{2}$ due to $q_{1}$ is given by:
$V = k \frac{q_{1}}{r}$
where $k$ is Coulomb's constant.
3. Work Done on Charge $q_{2}$ :
Now, we bring charge $q_{2}$ from infinity to the position where charge $q_{1}$ is located. The work done, $W_{2}$ , in this case is:
$W_{2} = q_{2} \cdot V = q_{2} \cdot (k \frac{q_{1}}{r}) = k \frac{q_{1} q_{2}}{r}$
4. Total Work Done:
The total work done $W$ to assemble the two charges from infinity is the sum of the work done on both charges:
$W = W_{1} + W_{2}$
Since $W_{1}$ is effectively zero (as we consider bringing $q_{1}$ from infinity in the absence of $q_{2}$ ), we focus on $W_{2}$ :
$W = 0 + k \frac{q_{1} q_{2}}{r} = k \frac{q_{1} q_{2}}{r}$
5. Potential Energy of the System:
Thus, the potential energy $U$ of the two-point charge system is given by:
$U = k \frac{q_{1} q_{2}}{r}$
Final Answer:
The potential energy of the two-point charge system is:
$U = k \frac{q_{1} q_{2}}{r}$

Updated on:7/8/2024

Two point charges Q and $- Q / 4$ are separated by a distance $X$ . Then .
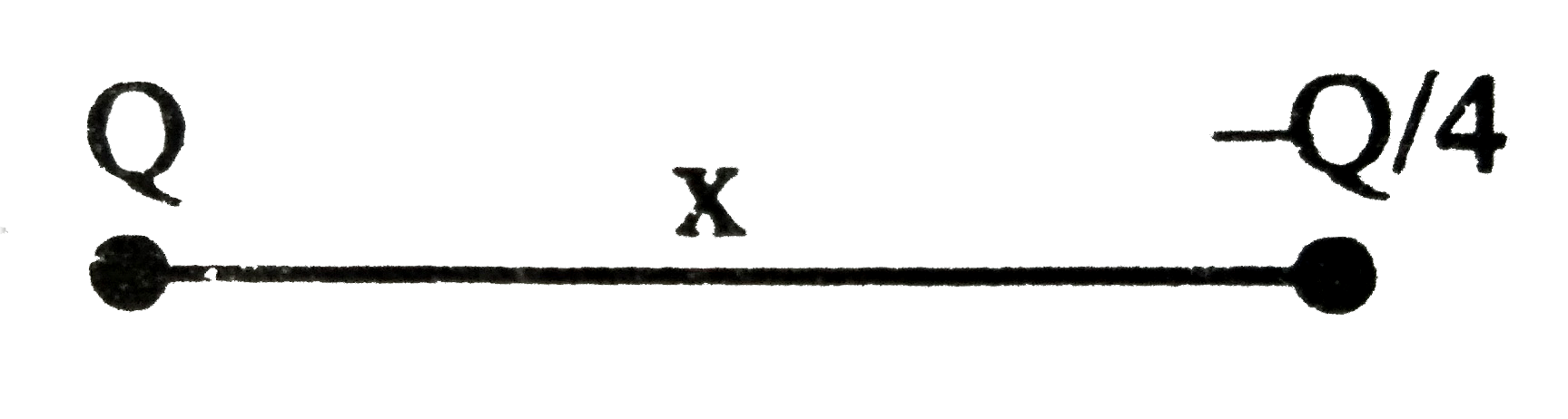Apotential is zero at a point on the axis which is $x / 3$ on the right side of the cahrge $- q / 4$
Bpotential is zero at a point on the axis which is $x / 5$ on the left side fo the charge $- Q / 4$
Celectric field is zero at a point on the axis which is at a distance $x$ on the right side fo the charge $- Q / 4$
Dthere exist two points on the axis where electric field is zero.
Magnitude of force between two point charges $q_{1}$ and $q_{2}$ which are separated by a distance r is given by
A $F = \frac{k | q_{1} q_{2} |}{r}$
B $F = \frac{k | q_{1} q_{2} | r}{r^{2}}$
C $F = k {(\frac{| q_{1} q_{2} |}{r})}^{2}$
D $F = \frac{k | q_{1} q_{2} |}{r^{2}}$