Point charge of 3×10−9C are situated at each of three corners of a square whose side is 15cm. The magnitude and direction of electric field at the vacant corner of the square is
2296V/m along the diagonal
9622V/m along the diagonal
22.0V/m along the diagonal
Zero
The correct Answer is:1
To solve the problem of finding the electric field at the vacant corner of a square with three point charges at the other corners, we can follow these steps:
Step 1: Understand the Configuration
We have a square with side length a=15cm=0.15m. There are three point charges of q=3×10−9C located at three corners of the square. Let's label the corners as A, B, C, and D, where D is the vacant corner.
Step 2: Calculate the Electric Field Due to Each Charge
The electric field E due to a point charge is given by the formula:
E=k⋅|q|r2
where k=9×109N m2/C2 is Coulomb's constant, q is the charge, and r is the distance from the charge to the point where we are calculating the electric field.
Electric Field at Corner D due to Charge at A (E_A)
- Distance rAD=a=0.15m
EA=9×109×3×10−9(0.15)2=27×1000.0225=1200N/C
- Direction: Away from charge A (towards corner D).
Electric Field at Corner D due to Charge at B (E_B)
- Distance rBD=a=0.15m
EB=9×109×3×10−9(0.15)2=1200N/C
- Direction: Away from charge B (towards corner D).
Electric Field at Corner D due to Charge at C (E_C)
- Distance rCD=√2a=0.15√2m
EC=9×109×3×10−9(0.15√2)2=27×1000.045=600N/C
- Direction: Away from charge C (towards corner D).
Step 3: Resolve the Electric Fields into Components
Since the electric fields due to charges at A and B are directed along the sides of the square, and the electric field due to charge C is directed diagonally, we can resolve these vectors.
- EA and EB are along the x and y axes respectively:
- EAx=1200N/C (to the right)
- EBy=1200N/C (upward)
- The electric field EC can be resolved into components:
ECx=EC⋅1√2=600⋅1√2=300√2N/C
ECy=EC⋅1√2=600⋅1√2=300√2N/C
Step 4: Sum the Components
Now we can sum the x and y components:
- Total Ex=EAx+ECx=1200+300√2
- Total Ey=EBy+ECy=1200+300√2
Step 5: Calculate the Resultant Electric Field
The magnitude of the resultant electric field E can be calculated using the Pythagorean theorem:
E=√(Ex)2+(Ey)2
Step 6: Calculate the Magnitude and Direction
Substituting the values:
Ex=1200+300√2≈1200+424.26≈1624.26N/C
Ey=1200+300√2≈1624.26N/C
E=√(1624.26)2+(1624.26)2=1624.26√2≈2297.0N/C
Step 7: Determine the Direction
The direction of the resultant electric field is along the diagonal of the square, pointing from the center towards the vacant corner D.
Final Answer
The magnitude of the electric field at corner D is approximately 2297N/C directed along the diagonal towards corner D.
---
We have a square with side length a=15cm=0.15m. There are three point charges of q=3×10−9C located at three corners of the square. Let's label the corners as A, B, C, and D, where D is the vacant corner.
The electric field E due to a point charge is given by the formula:
E=k⋅|q|r2
where k=9×109N m2/C2 is Coulomb's constant, q is the charge, and r is the distance from the charge to the point where we are calculating the electric field.
- Distance rAD=a=0.15m
EA=9×109×3×10−9(0.15)2=27×1000.0225=1200N/C
- Direction: Away from charge A (towards corner D).
- Distance rBD=a=0.15m
EB=9×109×3×10−9(0.15)2=1200N/C
- Direction: Away from charge B (towards corner D).
- Distance rCD=√2a=0.15√2m
EC=9×109×3×10−9(0.15√2)2=27×1000.045=600N/C
- Direction: Away from charge C (towards corner D).
Since the electric fields due to charges at A and B are directed along the sides of the square, and the electric field due to charge C is directed diagonally, we can resolve these vectors.
- EAx=1200N/C (to the right)
- EBy=1200N/C (upward)
ECx=EC⋅1√2=600⋅1√2=300√2N/C
ECy=EC⋅1√2=600⋅1√2=300√2N/C
Now we can sum the x and y components:
- Total Ex=EAx+ECx=1200+300√2
- Total Ey=EBy+ECy=1200+300√2
The magnitude of the resultant electric field E can be calculated using the Pythagorean theorem:
E=√(Ex)2+(Ey)2
Substituting the values:
Ex=1200+300√2≈1200+424.26≈1624.26N/C
Ey=1200+300√2≈1624.26N/C
E=√(1624.26)2+(1624.26)2=1624.26√2≈2297.0N/C
The direction of the resultant electric field is along the diagonal of the square, pointing from the center towards the vacant corner D.
The magnitude of the electric field at corner D is approximately 2297N/C directed along the diagonal towards corner D.
Topper's Solved these Questions
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:Level III (C.W)
Explore 55 Videos
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:Level 1
Explore 8 Videos
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:Level 1(C.W)
Explore 24 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:NARAYNAChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:ADDITIONAL PROBLEMS
Explore 14 Videos
- EXPERIMENTAL PHYSICSBook:NARAYNAChapter:EXPERIMENTAL PHYSICSExercise:Comprehension type
Explore 6 Videos
Similar Questions
Charges q,2q,3q and 4q are placed at the corners A,B,C and D of a square as shown in the following figure. The directon of electric field at the centre of the square is along
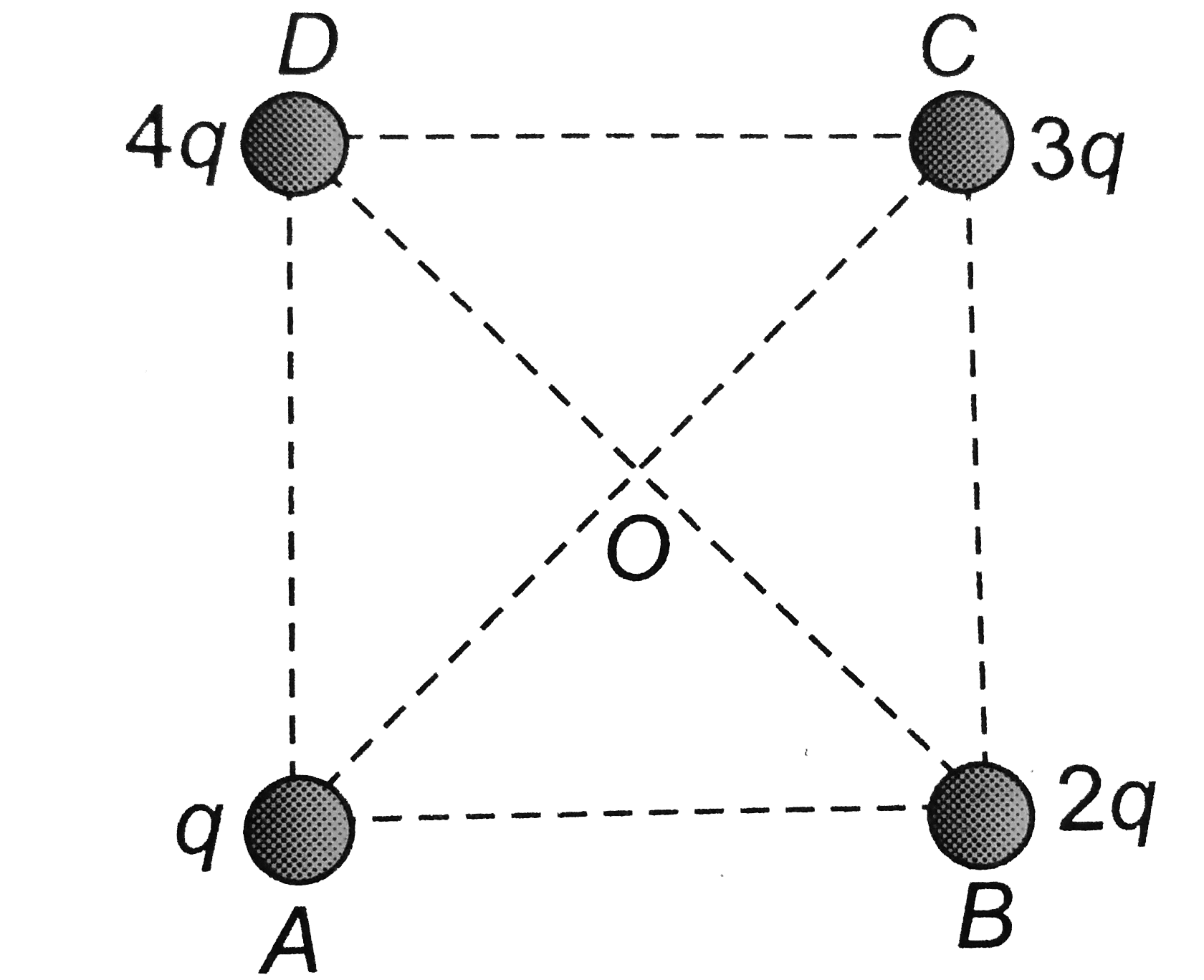
View SolutionThree charges, each equal to q, are placed at the three. corners of a square of side a . Find the electric field at. the fourth corner.
View Solution
Knowledge Check
Four charges are arranged at the corners of a square as shown in the figure. The direction of electric field at the centre of the square is along
 ADCBBCCABDAD
ADCBBCCABDADCharges of +103×10−9C are placed at each of the four corners of a square of side 8cm. The potential at the intersection of the diagonals is
A150√2 voltB1500√2 voltC900√2 voltD900 voltFour point charge are placed at the corners of a square with diagonal 2a as shown. What is the total electric field at the center of the squre?
 Akq/a2 at an angle 45∘ above the +x-axisBkq/a2 at an angle 45∘ above the -x-axisC3kq/a2 at an angle 45∘ above the -x-axisD3kq/a2 at an angle 45∘ above the +x-axis
Akq/a2 at an angle 45∘ above the +x-axisBkq/a2 at an angle 45∘ above the -x-axisC3kq/a2 at an angle 45∘ above the -x-axisD3kq/a2 at an angle 45∘ above the +x-axis
Equal charges of +4μC are placed at the three corners of an equilateral triangle of side 2m. Calculate the magnitude and direction of the force on one of the charges.
View SolutionFour charges of same magnitude and same sign are placed at the corners of a square, of each side0⋅1m. What is electric field intensity at the center of the square?
View SolutionFour charges are placed at the corners of a square of side 10 cm as shown in figure. If q is 1μC, then what will be electric field intensity at the centre of the square?

View SolutionFour point charges of +1μc each are placed on the four corners of a square of side 1 m. Calculate the electric potential at the centre of the square.
View SolutionConsider four equal charges (q, each) placed on the corners of a square with side a. Determine the magnitude and direction of the resultant force on the charge on lower right corner.
View Solution

