Two identical particles of charge q each are connected by a masless spring of force cosntant k .They are placed over a smoothe horizontal surface .They are released wheen unstretched .If maximum extneison of the spring is r,the value of k is :(neglect gravitational effect)
k=qr√1πε0r
k=14πε0q2l2×1r
k=2qr√1πε0r
k=qr√2πε0r
The correct Answer is:2
To solve the problem, we will analyze the forces acting on the two identical charged particles connected by a massless spring when they are released from an unstretched position.
1. Understanding the Setup:
- We have two identical particles, each with charge q, connected by a massless spring of spring constant k.
- The particles are placed on a smooth horizontal surface and are released from an unstretched position.
2. Identifying Forces:
- When the particles are released, they will repel each other due to the electrostatic force (Coulomb's force) between them.
- The electrostatic force Fc acting on each particle is given by Coulomb's law:
Fc=ke⋅q2r2
where ke=14πϵ0 is Coulomb's constant, and r is the distance between the two charges when the spring is maximally extended.
3. Maximum Extension of the Spring:
- Let r be the maximum extension of the spring. At this point, the spring force Fs is equal to the electrostatic force Fc.
- The spring force is given by Hooke's law:
Fs=k⋅r
4. Setting Forces Equal:
- At maximum extension, the spring force equals the electrostatic force:
k⋅r=ke⋅q2r2
5. Rearranging the Equation:
- Rearranging the equation gives:
k=ke⋅q2r3
6. Substituting for Coulomb's Constant:
- Substitute ke=14πϵ0:
k=14πϵ0⋅q2r3
7. Final Expression:
- Therefore, the value of the spring constant k in terms of the charges and the maximum extension is:
k=14πϵ0⋅q2r3
Summary:
The final expression for the spring constant k is:
k=14πϵ0⋅q2r3
- We have two identical particles, each with charge q, connected by a massless spring of spring constant k.
- The particles are placed on a smooth horizontal surface and are released from an unstretched position.
- When the particles are released, they will repel each other due to the electrostatic force (Coulomb's force) between them.
- The electrostatic force Fc acting on each particle is given by Coulomb's law:
Fc=ke⋅q2r2
where ke=14πϵ0 is Coulomb's constant, and r is the distance between the two charges when the spring is maximally extended.
- Let r be the maximum extension of the spring. At this point, the spring force Fs is equal to the electrostatic force Fc.
- The spring force is given by Hooke's law:
Fs=k⋅r
- At maximum extension, the spring force equals the electrostatic force:
k⋅r=ke⋅q2r2
- Rearranging the equation gives:
k=ke⋅q2r3
- Substitute ke=14πϵ0:
k=14πϵ0⋅q2r3
- Therefore, the value of the spring constant k in terms of the charges and the maximum extension is:
k=14πϵ0⋅q2r3
The final expression for the spring constant k is:
k=14πϵ0⋅q2r3
Topper's Solved these Questions
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:Level III (C.W)
Explore 55 Videos
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:Level 1
Explore 8 Videos
- ELECTROSTATICS AND GAUSS LAWBook:NARAYNAChapter:ELECTROSTATICS AND GAUSS LAWExercise:Level 1(C.W)
Explore 24 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:NARAYNAChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:ADDITIONAL PROBLEMS
Explore 14 Videos
- EXPERIMENTAL PHYSICSBook:NARAYNAChapter:EXPERIMENTAL PHYSICSExercise:Comprehension type
Explore 6 Videos
Similar Questions
Two blocks A and B of mass m and 2m respectively are connected by a light spring of force constant k. They are placed on a smooth horizontal surface. Spring is stretched by a length x and then released. Find the relative velocity of the blocks when the spring comes to its natural length

View SolutionTwo blocks A and B of masses m and 2m, respectively , are connected by a massless spring of force constant k and are placed on a smooth horizontal plane. The spring is stretched by an amount x and then released . The relative velocity of the blocks when the spring comes to its natural length is

View Solution
Knowledge Check
Two identical particles of charge q each are connected by a massless spring of force constant k. They are placed over a smooth horizontal surface. They are released when the separation between them is r and spring is unstretched. If maximum extension of the spring is r, the value of k is (neglect gravitational effect)
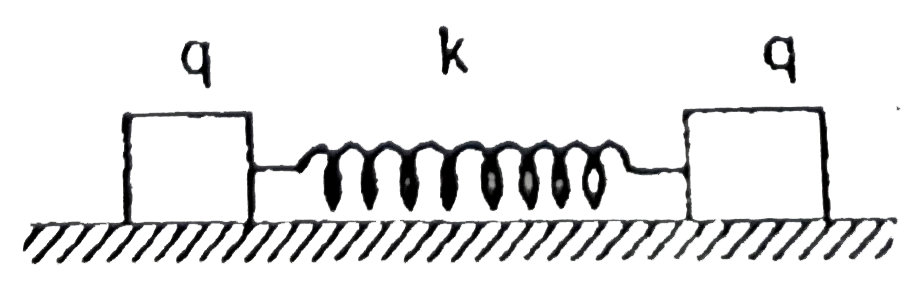 Aq24πε0r2Bq22πε0r3Cq2πε0r3Dnone of these
Aq24πε0r2Bq22πε0r3Cq2πε0r3Dnone of theseTwo identical particle each of mass m are inter connects by a light spring of stiffness k ,the time period for small oscillation is equal to
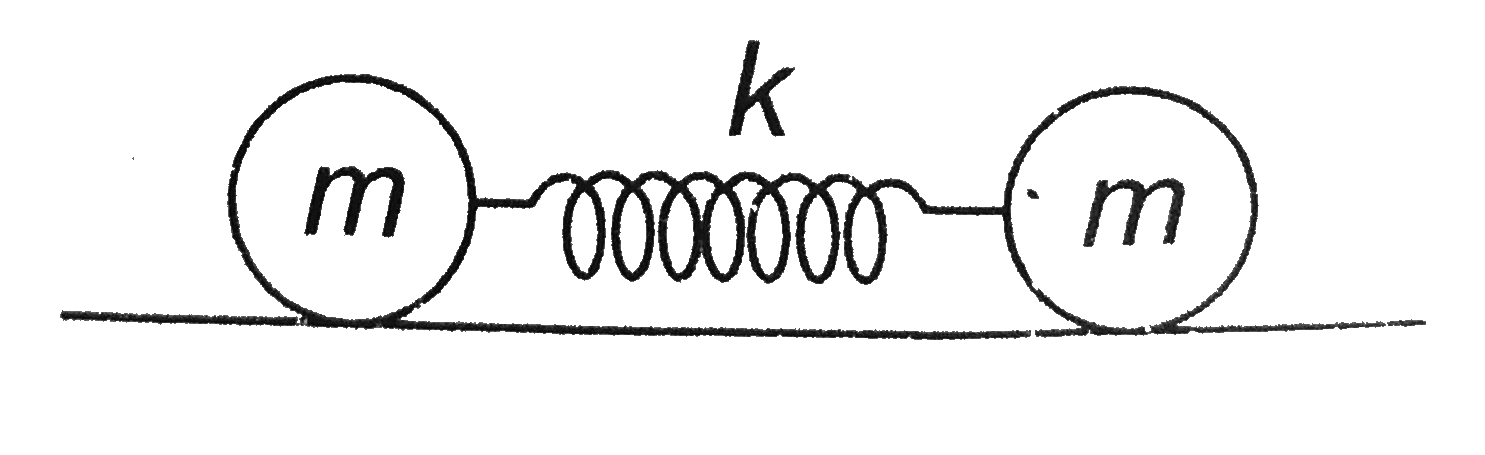 A2π√mkBπ2√mkCπ√m2kDπ√2mk
A2π√mkBπ2√mkCπ√m2kDπ√2mkTwo blocks of masses m1 and m2 are connected by a massless spring and placed on smooth surface. The spring initially stretched and released. Then :
Athe momentum of each particle remains constant separatelyBthe magnitude of momentums of each body are equal to each otherCthe mechanical energy of system remains constantDboth (C) and (B) are correct
Two blocks A and B of mass m and 2m respectively are connected by a massless spring of spring constant K. This system lies over a smooth horizontal surface. At t=0 the bolck A has velocity u towards right as shown while the speed of block B is zero, and the length of spring is equal to its natural length at that at that instant.

Column IColumn II(A)The velocity of block A(P)can never be zero(B)The velocity of block B(Q)may be zero at certain instants of time(C)The kinetic energy of system of two block(R)is minimum at maximum compression of spring(D)The potential energy of spring(S)is maximum at maximum extension of spring
View SolutionTwo blocks of masses m1 and m2 are connected by an ideal sprit, of force constant k. The blocks are placed on smooth horizontal surface. A horizontal force F acts on the block m1. Initially spring is relaxed, both the blocks are at rest.

What is acceleration of centre of mass of system at the instant of maximum elongation of spring
View SolutionTwo blocks of masses m1 and m2 are connected by an ideal sprit, of force constant k. The blocks are placed on smooth horizontal surface. A horizontal force F acts on the block m1. Initially spring is relaxed, both the blocks are at rest.
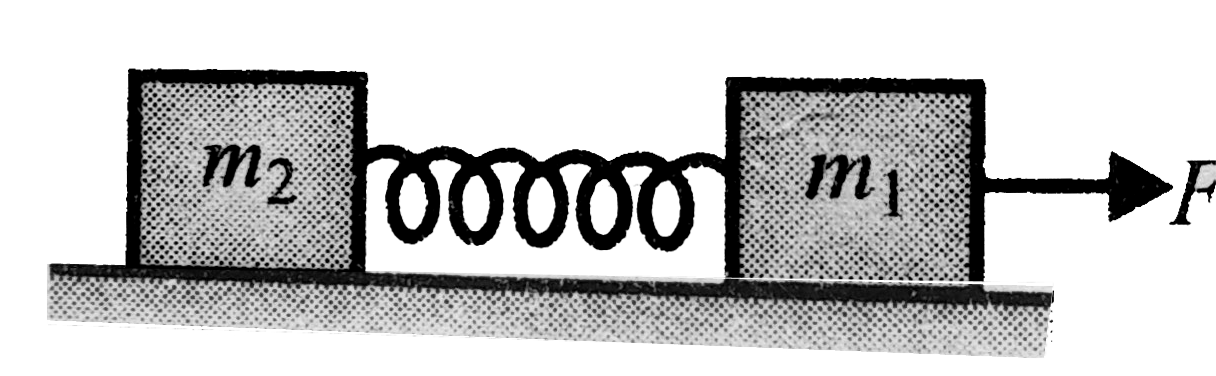
What is maximum elongation of spring.
View SolutionBlocks A&B of mass m each are connected with spring of constant k both blocks lie on frictionless ground and are imparted horizontal velocity v as shown when spring is unstretched find the maximum stretch of spring.

View SolutionA solid uniform cylinder of mass M attached to a massless spring of force constant k is placed on a horizontal surface in such a way that cylinder can roll without slipping. If system is released from the stretched position of the spring, then the period will be-
_E01_059_Q01.png)
View Solution

