Three charge −q,+q and −q are kept at the veticles of an equllateral triangle of 10cm side.The potential at the mid point in between −q,−q, if q=5μC is
−6.4×105V
−12.8×104V
−6.4×104V
−12.8×105V
The correct Answer is:4
To find the electric potential at the midpoint between the two charges −q in an equilateral triangle configuration, we can follow these steps:
Step 1: Understand the Configuration
We have three charges located at the vertices of an equilateral triangle:
- Charge A=−q
- Charge B=+q
- Charge C=−q
The side length of the triangle is L=10cm=0.1m. We need to find the potential at the midpoint D of the line segment joining charges B and C.
Step 2: Calculate Distances
The distance from point D to charge B and charge C is:
BD=CD=L2=0.12=0.05m
The distance from point D to charge A can be calculated using the properties of the equilateral triangle:
AD=L⋅sin(60∘)=0.1⋅√32=0.05√3m
Step 3: Calculate the Electric Potential
The electric potential V at point D due to a point charge is given by:
V=kqr
where k=9×109N m2/C2 is Coulomb's constant, q is the charge, and r is the distance from the charge to the point where we are calculating the potential.
Potential at D due to each charge:
1. Due to charge A (which is −q):
VA=k−qAD=9×109⋅−5×10−60.05√3=−45×103√3V
2. Due to charge B (which is +q):
VB=kqBD=9×109⋅5×10−60.05=9×109⋅10−4=90V
3. Due to charge C (which is −q):
VC=k−qCD=9×109⋅−5×10−60.05=−90V
Step 4: Total Potential at Point D
Now, we sum the potentials due to all three charges:
VD=VA+VB+VC
Substituting the values:
VD=(−45×103√3+90−90)V
Since VB and VC cancel each other out:
VD=−45×103√3V
Step 5: Calculate the Numerical Value
Calculating VD:
VD≈−45×103⋅0.577≈−26.9×103V≈−26.9kV
Final Answer
Thus, the potential at the midpoint D is approximately:
−26.9kV
We have three charges located at the vertices of an equilateral triangle:
- Charge A=−q
- Charge B=+q
- Charge C=−q
The distance from point D to charge B and charge C is:
BD=CD=L2=0.12=0.05m
The distance from point D to charge A can be calculated using the properties of the equilateral triangle:
AD=L⋅sin(60∘)=0.1⋅√32=0.05√3m
The electric potential V at point D due to a point charge is given by:
V=kqr
where k=9×109N m2/C2 is Coulomb's constant, q is the charge, and r is the distance from the charge to the point where we are calculating the potential.
1. Due to charge A (which is −q):
VA=k−qAD=9×109⋅−5×10−60.05√3=−45×103√3V
VB=kqBD=9×109⋅5×10−60.05=9×109⋅10−4=90V
VC=k−qCD=9×109⋅−5×10−60.05=−90V
Now, we sum the potentials due to all three charges:
VD=VA+VB+VC
Substituting the values:
VD=(−45×103√3+90−90)V
Since VB and VC cancel each other out:
VD=−45×103√3V
Calculating VD:
VD≈−45×103⋅0.577≈−26.9×103V≈−26.9kV
Thus, the potential at the midpoint D is approximately:
−26.9kV
Topper's Solved these Questions
- ELECTROSTATICS AND GAUSS LAWBOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Level III (C.W)
55 Videos
- ELECTROSTATICS AND GAUSS LAWBOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Level 1
8 Videos
- ELECTROSTATICS AND GAUSS LAWBOOK - NARAYNACHAPTER - ELECTROSTATICS AND GAUSS LAWEXERCISE - Level 1(C.W)
24 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBOOK - NARAYNACHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCEEXERCISE - ADDITIONAL PROBLEMS
14 Videos
- EXPERIMENTAL PHYSICSBOOK - NARAYNACHAPTER - EXPERIMENTAL PHYSICSEXERCISE - Comprehension type
6 Videos
Similar Questions
Knowledge Check
Three charges 2q,−q,and−q are located at the vertices of an equilateral triangle. At the center of the triangle,
Athe field is zero but potential is nonzero.Bthe field is nonzero but potential is zero.Cboth field and potential are zero.Dboth field and potential are nonzero.Three charge −q,+q and −q are placed at the cornors of an equilateral triangle of side a The resultant electric froce an a charge +q placed at a the centroid O of the triangle is
A3q24πε0a2Bq24πε0a2Cq22πε0a2D3q22πε0a2Three charges Q,(+q) and (+q) are placed at the vertices of an equilateral triangle of side l as shown in the figure. It the net electrostatic energy of the system is zero, then Q is equal to
 A(−q2)B(−q)C(+q)DZero
A(−q2)B(−q)C(+q)DZero
Three charges +q,2qand−4q are placed on the three vertices of an equale-laterail triangle of each side0⋅1m. Calculate electrostatic potential energy of the system, take q=10−7C
View SolutionThree point charges q,−4q and 2q are placed at the vertices of an equilateral triangle ABC of side 'l' as shown in the Fig. Obtain the experssion for the magnitude of the resultant electric force acting on the charge q.
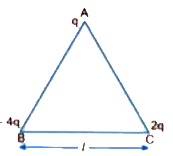
View SolutionThree charges -q +q and +q are placed at the corner of the equilateral triangle of side a as shown in the figure.The net electric potential at the centroid of the triangle will be (k=(1)/(4 pi varepsilon_(0)))
View Solution(a) Three point charges q,-4q and 2q are placed at the vertices of an equilateral triangle ABC of side 'l' as shown in the figure. Obtain the expression for the magnitude of the resultant electric force acting on the charge q.
(b) Find out the amount of the work 4one to separate the charges at infinite distance.

View SolutionCharges +q−4q and +2q are arranged at the corners of an equilatoral triangle of side 0.15m.If the q=1μC their mutual potential energy is
View Solution
