In the previous problem , sphere A is moving with speed u1 and sphere B with speed u2 in opposite direction. After the collision , sphere A comes to rest , then u1/u2 is
1−e1+e
1+e1−e
e1+e
2e1+e
The correct Answer is:B
mu1−mu2=mv1+mv2 (i)
v1−v2=−e(u1−u2) [use velocities with sign]
v1−v2=−e{u1−u2} (ii)
v1+v2=u1−u2 (i)
v1−v2=−e(u1+u2) (ii)
Given , v1=0 , by solving , we get
u1u2=1+e1−e
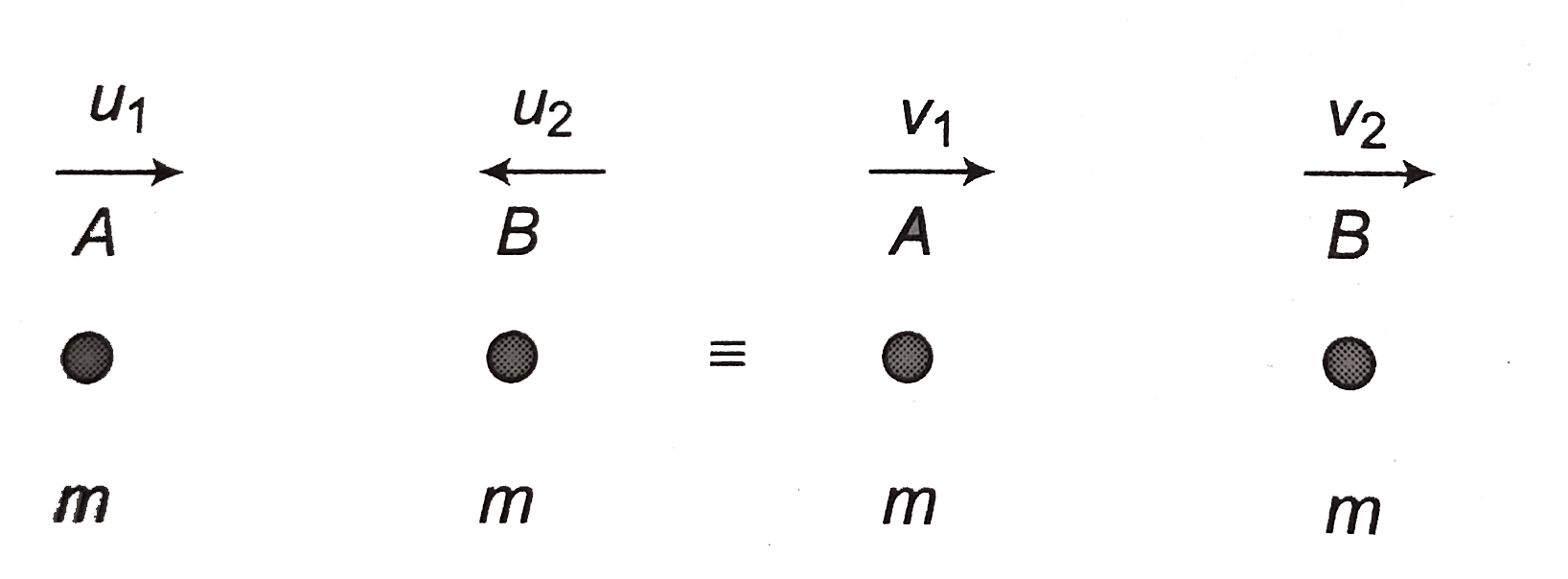
Topper's Solved these Questions
Similar Questions
Knowledge Check
An object of mass 500 g moving with a speed of 10 m s−1 collides with another object of mass 250 g moving with a speed of 2 m s−1 in the opposite direction. After collision both the objects move in the same direction with common velocity. Write the proper order of steps to find out their common velocity after collision.
(a) Calculate the total momentum of two bodies before collision as m1u1+m2u2.
(b) Write down the given values of m1 and m2 in SI system
(c ) Write the expression for their total momentum after collision as (m1+m2) v where v is their common velocity.
(d) Assign proper signs to the initial velocities u1 and u2.
(e) Using law of conservation of momentum Equate the above two expressions and determine the value of v as m1u1+m2u2m1+m2Ab d a c eBb d c e aCa d b c eDc d e b aA particle of mass m moving with velocity u1 collide elastically with another particle of same mass moving with velocity u2 in the same direction. After collision their speeds are v1 and v2 respectively then
(A) u1+v1=v2+u2, (B) u1−v1=v2+u2ABoth the equations A and B are correctBBoth the equation A and B are incorrectCEquation A is correct but not BDEquation B is correct but not AAn object of mass 500 g moving with a speed of 10 m s−1 collides with another object of mass 250 g moving with a speed of 2 m s−1 in the opposite direction. After collision both the objects move in the same direction with common velocity. Write the proper order of steps to find out their common velocity after collision.
(a) Calculate the total momentum of two bodies before collision as m1u1+m2u2.
(b) Write down the given values of m1 and m2 in SI system
(c ) Write the expression for their total momentum after collision as (m1+m2) v where v is their common velocity.
(d) Assign proper signs to the initial velocities u1 and u2.
(e) Using law of conservation of momentum Equate the above two expressions and determine the value of v as m1u1+m2u2m1+m2AB D A C EBA D B C ECB D C E ADC D E B A
A ball A moving with velocity u, impinges directly on an equal ball B moving with velocity v in the opposite direction. If the coefficient of elasticity is e and after impact ball A comes to rest, then uv=1+e1−e.
View SolutionRelative speed of two persons moving with u m/s and v m/s in same direction where u>v
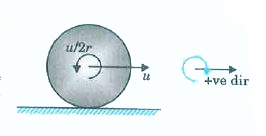
View SolutionState of motion of the sphere at t = 0 is described in figure, Centre of the sphere is moving towards right with a speed u and angular velocity of the sphere is u/2r in the anticlockwise sense. Here is the radius of sphere. We can understand that it is a case of slipping and after some time sphere starts pure rolling due to friction from the surface. We can assume direction towards right as positive and thus clockwise sense should be treated positive for rotational motion. Assume ng coefficient of friction between sphere and the surface. Mass of sphere is m.

What will be the speed of sphere when it starts pure rolling?
View SolutionState of motion of the sphere at t = 0 is described in figure, Centre of the sphere is moving towards right with a speed u and angular velocity of the sphere is u/2r in the anticlockwise sense. Here r is the radius of sphere. We can understand that it is a case of slipping and after some time sphere starts pure rolling due to friction from the surface. We can assume direction towards right as positive and thus clockwise sense should be treated positive for rotational motion. Assuming coefficient of friction between sphere and the surface. Mass of sphere is m.
At what time sphere stops rotating for a moment?
View SolutionState of motion of the sphere at t = 0 is described in figure, Centre of the sphere is moving towards right with a speed u and angular velocity of the sphere is u/2r in the anticlockwise sense. Here is the radius of sphere. We can understand that it is a case of slipping and after some time sphere starts pure rolling due to friction from the surface. We can assume direction towards right as positive and thus clockwise sense should be treated positive for rotational motion. Assume ng coefficient of friction between sphere and the surface. Mass of sphere is m.
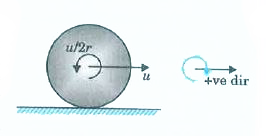
At what time sphere starts pure rolling?
View Solution

