Particle 1 experiences a perfectly collision with a staionary particle 2. Determine their mass ratio , if the particles move perpendicularly to each other.
Momentum conservation
x−axis:m1u+m2×0=m1v1cosθ+m2v2cos(90−θ) (i)
y−axis:0=m1v1sinθ−m2v2sin(90−θ) (ii)
Ki=Kf
12m1u2=12m1v21+12m2v22 (iii)
Solving , m1m2=1
The calculations will be simple if we do not break momentum in two directions.
We know , p=mv,K=12mv2,K=p22m
Resultant momentum after the collision should be along the x-axis.
By the momentum conservation :
p=√p21+p22⇒p2=p21+p22 (i)
Since the collision is elastic , Ki=Kf
p22m1=p212m1+p222m2 (iii)
p21+p222m1=p212m1+p222m2⇒m1m2=1


Topper's Solved these Questions
Similar Questions
Particle 1 experiences a perfectly elastic collision with a stationary particle 2. Determine their mass ratio , if the particles fly symmetrically relative to the initial motion direction particle 1 with angle of divergence θ=60∘.
View SolutionParticle 1 experiences a perfectly elastic collision with a stationary particle 2. Determine their mass ratio, if
(a) after a head-on collision the particles fly apart in the opposite directions with equal velocities,
(b) the particles fly apart symmetrically relative to the initial motion direction of particle I with the angle of divergence θ=60∘.
View Solution
Knowledge Check
Particle A makes a perfectly elastic collision with another particle B at rest. They fly apart in opposite directions with equal speeds. The ratio of their masses mA/mB is
A12B13C14D1√3A particle of mass m1 moving with a velocity of 5 ms−1 collides head on with a stationary particle of mass m2. After collision both the particle move with a common velocity of 4ms−1then the value of m1/m2is :
A4:1B2:1C1:8D1:1
A particle of mass m1 experienced a perfectly elastic collision with a stationary particle of mass m2. What fraction of the kinetic energy does the striking particle lose, if
(a) it recoils at right angles to its original motion direction,
(b) the collision is a head-on one?
View SolutionA particle of mass m1 experiences a perfectlly elastic collision with a stationary particle of mass m2. Match the entires in column I to all the entires in column II.
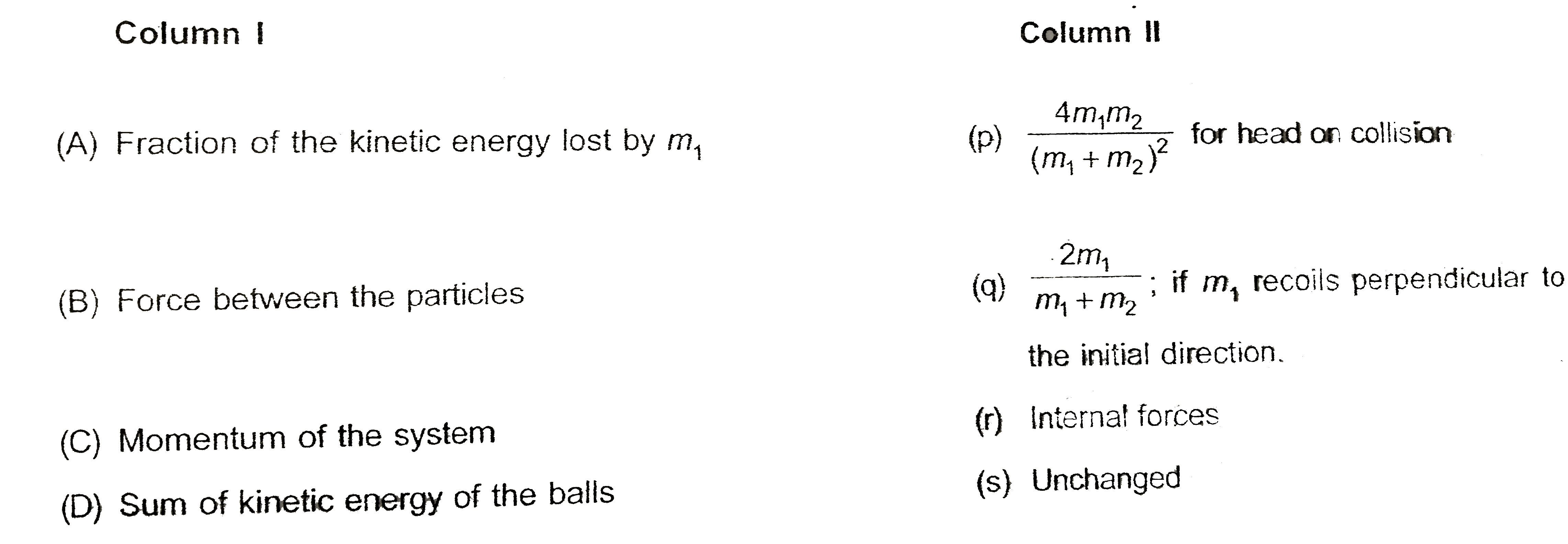
View SolutionParticle 1 moving with velocity v=10m/s experienced a head-on collision with a stationary particle 2 of the same mass. As a result of the collision, the kinetic energy of the system decreased by η=1.0%. Find the magnitude and direction of the velocity of particle 1 after the collision.
View SolutionIn a perfectly elastic collision in two dimensions between two particles of ………………….mass,the two particles move at …………………..to each other.
View SolutionA particle 1 moving with velocity v=10m/s experienced a head on collision with a stationary particle 2 of the same mass. As a result of collision, the kinetic energy of the system decreased by 50%. Find the magnitude and direction of the velocity of the particle 1 after collision.
View SolutionA particle of mass m1, hits another particle in rest of mass m2, obliquely, If both the particles after elastic collision moves perpendicular to each other then m1m2 is
View Solution
