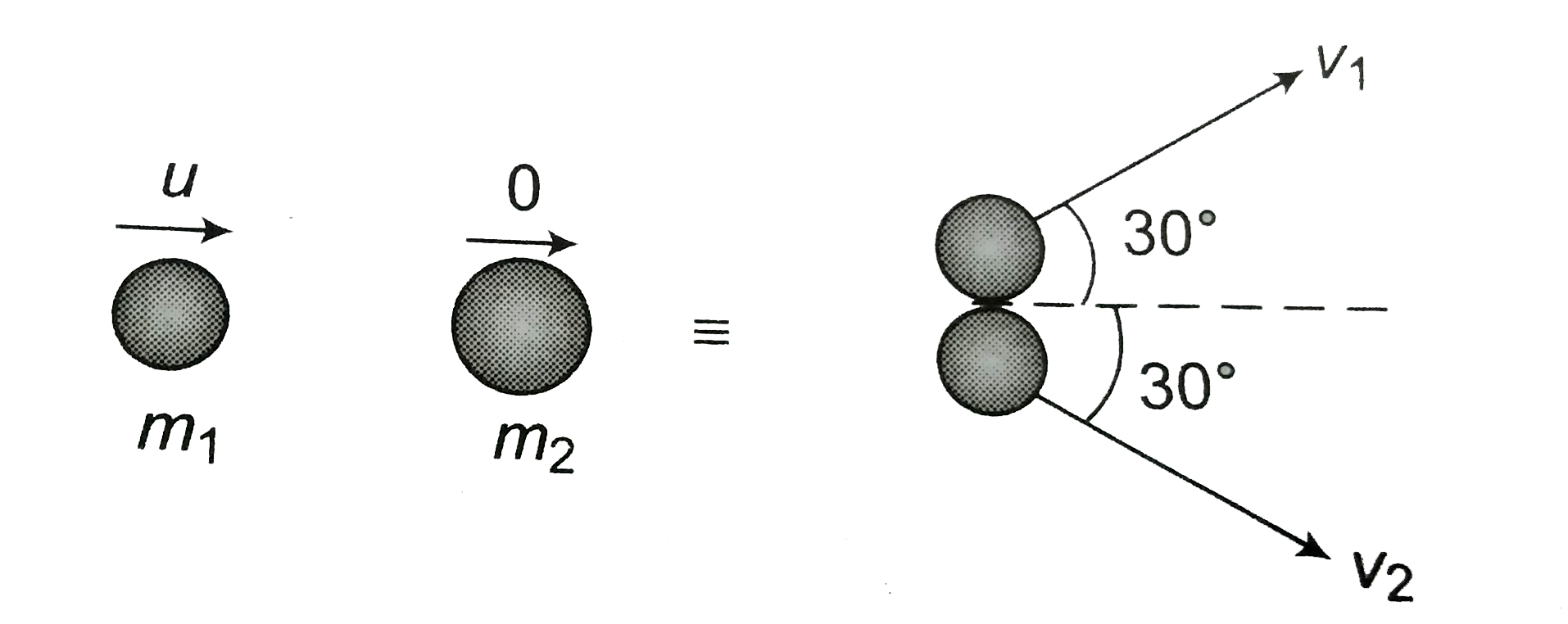
Particle $1$ experiences a perfectly elastic collision with a stationary particle $2$ . Determine their mass ratio , if the particles fly symmetrically relative to the initial motion direction particle $1$ with angle of divergence $θ = 60^{\circ}$ .

Video Solution

Text Solution

Verified by Experts

By the momentum conservation :
$x - a x i s : m_{1} u = m_{1} v_{1} {cos 30}^{\circ} + m_{2} v_{2} {cos 30}^{\circ}$ (i)
$y - a x i s : 0 = m_{1} v_{1} {sin 30}^{\circ} - m_{2} v_{2} {sin 30}^{\circ}$ (ii)
$\Rightarrow m_{1} v_{1} = m_{2} v_{2}$ in (i)
$m_{1} u = m_{1} u = m_{1} v_{1} {cos 30}^{\circ} + m_{1} v_{1} {cos 30}^{\circ}$
$= 2 m_{1} v_{1} {cos 30}^{\circ} = \sqrt{3} m_{1} v_{1}$
$v_{1} = \frac{μ}{\sqrt{3}}$
$v_{2} = \frac{m_{1}}{m_{2}} v_{1} = (\frac{m_{1}}{m_{2}}) \frac{u}{\sqrt{3}}$
Since the collision is elastic , $K_{i} = K_{f}$
$\frac{1}{2} m_{1} u^{2} = \frac{1}{2} m_{1} v_{1}^{2} + \frac{1}{2} m_{2} v_{2}^{2}$
$m_{1} u^{2} = m_{1} {(\frac{u}{\sqrt{3}})}^{2} + m_{2} \times {(\frac{m_{1}}{m_{2}})}^{2} {(\frac{u}{\sqrt{3}})}^{2}$

Updated on:21/07/2023