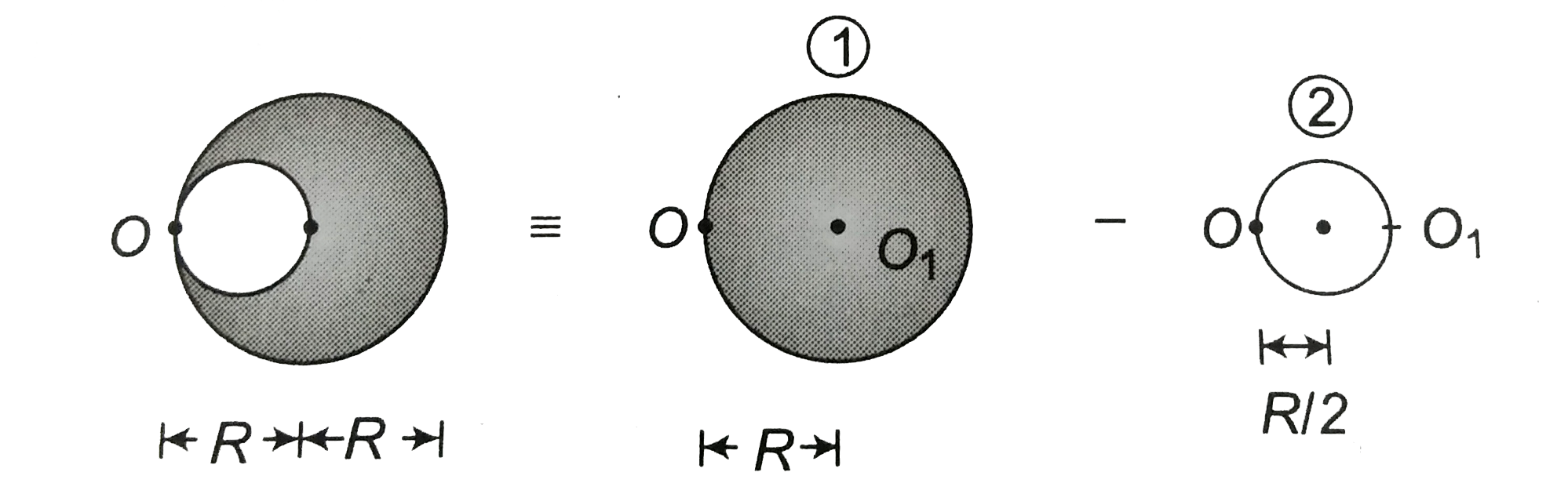
From a circular disc of radius R, another disc of diameter R is remove

From a circular disc of mass $M$ and radius $R$ , a part of $60^{\circ}$ is removed. The $M . I .$ of the remaining portion of disc about an axis passing through the center and perpendicular to plane of disc is

A $\frac{5}{6} M R^{2}$
B $\frac{5}{3} M R^{2}$
C $\frac{5}{12} M R^{2}$
D $\frac{5}{24} M R^{2}$
Out of a disc of mass M and radius R a concentric disc of mass m and radius r is removed. The M.I. of the remaining part about the symmetric axis will be :
A $(M - m) {(R + r)}^{2} / 2$
B $(M - m) (R^{2} - r^{2}) / 2$
C $(M - m) {(R - r)}^{2} / 2$
D $(M - m) (R^{2} + r^{2}) / 2$
From a circular disc of radius R and mass 9M, a small disc of radius R/3 is removed from the disc. The moment of inertia of the remaining disc about an axis perpendicular to the plane of the disc and passing through O is

A $4 M^{2}$
B $\frac{40}{9} M R^{2}$
C $10 M R^{2}$
D $\frac{37}{9} M R^{2}$

From a circular disc of radius $R$ , another disc of diameter $R$ is removed. Locate $c . m .$ of the remaining portion.