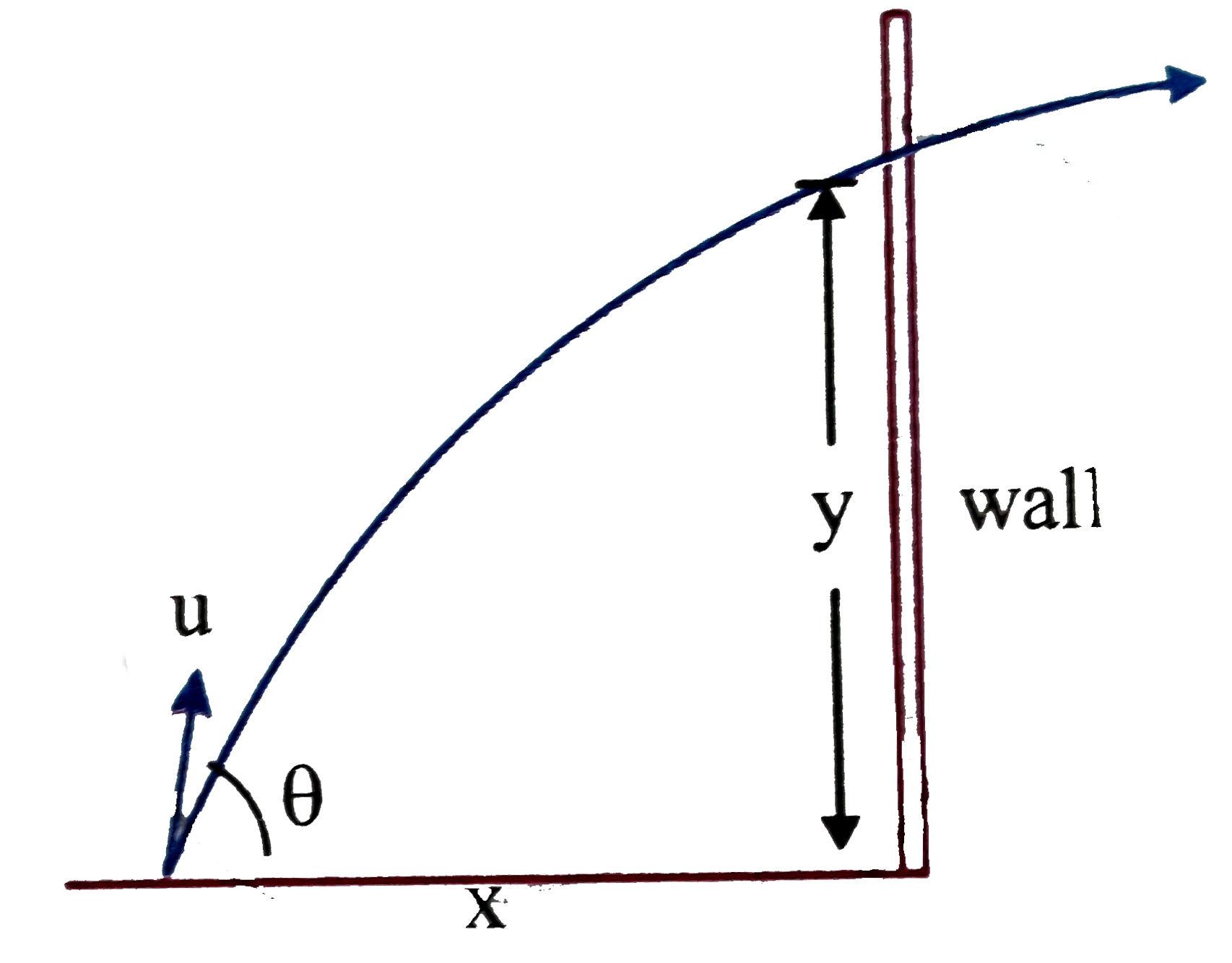
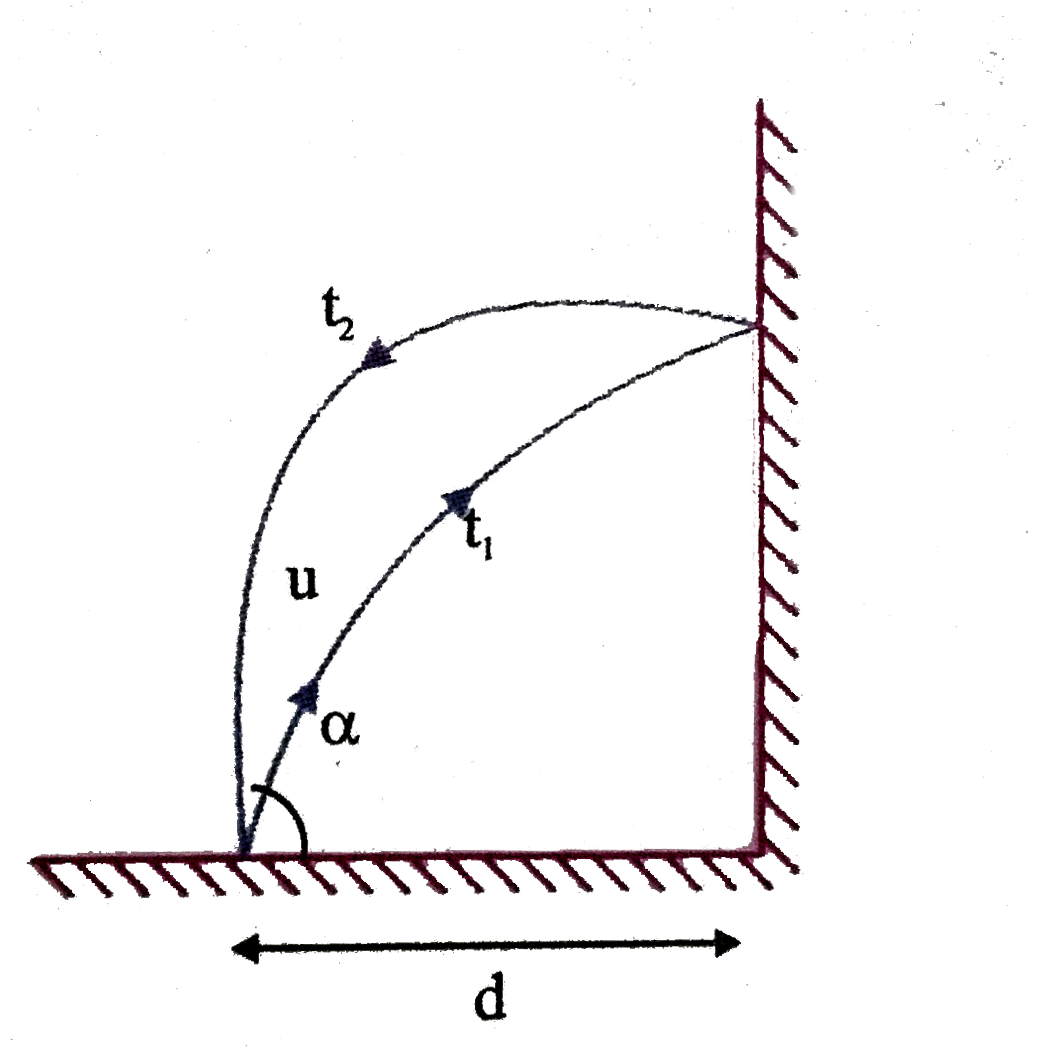
A shot is fired with a velocity $u$ at a very high vertical wall whose distance from the point of projection is $x$ .The greatest height above the level of the point of projection at which the bullet can hit the wall is.

$\frac{u^{4} + g^{2} x^{2}}{2 g u^{2}}$

$\frac{u^{4} - g^{2} x^{2}}{g u^{2}}$

$\frac{u^{4} - g^{2} x^{2}}{4 g u^{2}}$

$\frac{u^{4} - g^{2} x^{2}}{2 g u^{2}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Let $θ$ the angle of projection, suppose $y$ is the height at which bullet hit the wall.We have, from equation of trajectory.
$y = x \tan θ - \frac{g x^{2} \sec^{2} θ}{2 u^{2}}$ ----(i)
$\frac{d y}{d θ} = x \sec^{2} θ - \frac{g x^{2}}{2 u^{2}} 2 \sec θ (\sec θ \tan θ)$
$= x \sec^{2} θ [1 - \frac{x g \tan θ}{u^{2}}] = 0 or \tan θ = \frac{u^{2}}{g x}$
Substituting this value in equation (i), we get
$y_{max} = x \frac{u^{2}}{g x} - \frac{1}{2} \frac{g x^{2}}{u^{2}} [1 - \frac{u^{4}}{x^{2} g^{2}}]$
$= \frac{u^{2}}{g} - \frac{g x^{2}}{2 u} - \frac{u^{2}}{2 g} = \frac{2 u^{4} - g^{2} x^{2} - u^{4}}{2 u^{2} g}$ or $y_{max} = \frac{u^{4} - g^{2} x^{2}}{2 g u^{2}}$

Updated on:21/07/2023

Class 11 PHYSICS PROJECTILE MOTION

Topper's Solved these Questions

Knowledge Check

A ball is projected from the ground with speed u at an angle $α$ with horizontal. It collides with a wall at some distance from the point of projection and returns on the same level. Coefficient of restitution between the ball and the wall is e, then time taken in path AB and maximum height attained by the ball is

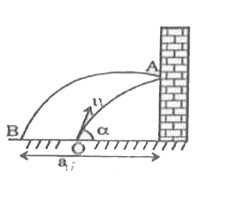A $\frac{a}{e u cos α}, \frac{u^{2} {sin}^{2} α}{2 g}$
B $\frac{a}{u cos α}, \frac{u^{2} {sin}^{2} α}{2 g}$
C $\frac{a}{e u cos α}, \frac{u^{2} {sin}^{2} α}{2 g}$
D $\frac{a}{u cos α}, \frac{u^{2} {sin}^{2} α}{2 g}$
An inelastic ball is projetced with a velocity $' u'$ at an angle $' α'$ to the horizontal, towards a wall distant $' d'$ from the point of projection. After collision the ball returns to the point of projection (Co-efficient of restitution between sphere and wall is $' e'$ )

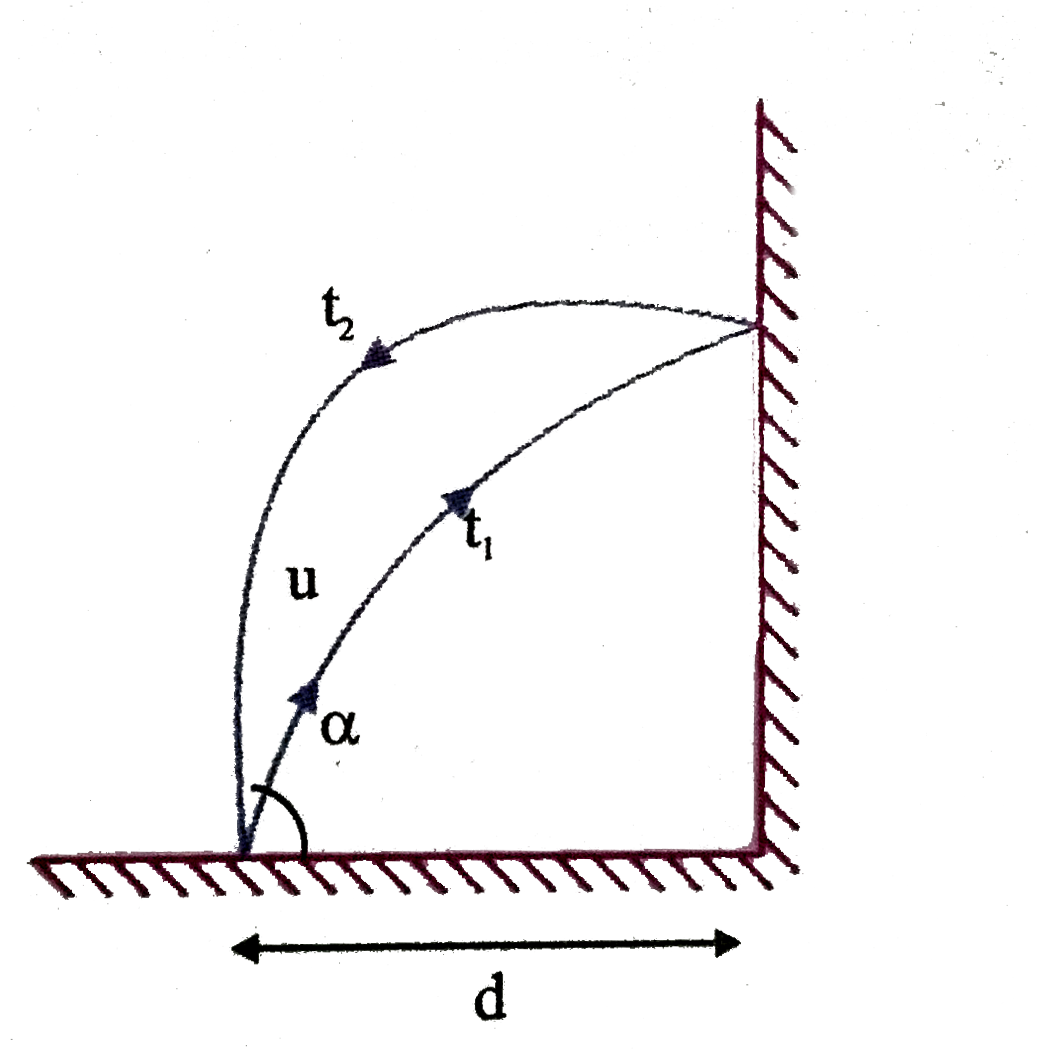
The horizontal distance $' d'$ from the wall is
A $\frac{u^{2} sin 2 α}{g} (\frac{e}{1 + e})$
B $\frac{u^{2} sin α}{g} (\frac{e}{1 + e})$
C $\frac{u^{2} cos 2 α}{g} (\frac{e}{1 + e})$
D $\frac{u^{2} sin 2 α}{2 g} (\frac{e}{1 + e})$
An inelastic ball is projetced with a velocity $' u'$ at an angle $' α'$ to the horizontal, towards a wall distant $' d'$ from the point of projection. After collision the ball returns to the point of projection (Co-efficient of restitution between sphere and wall is $' e'$ )

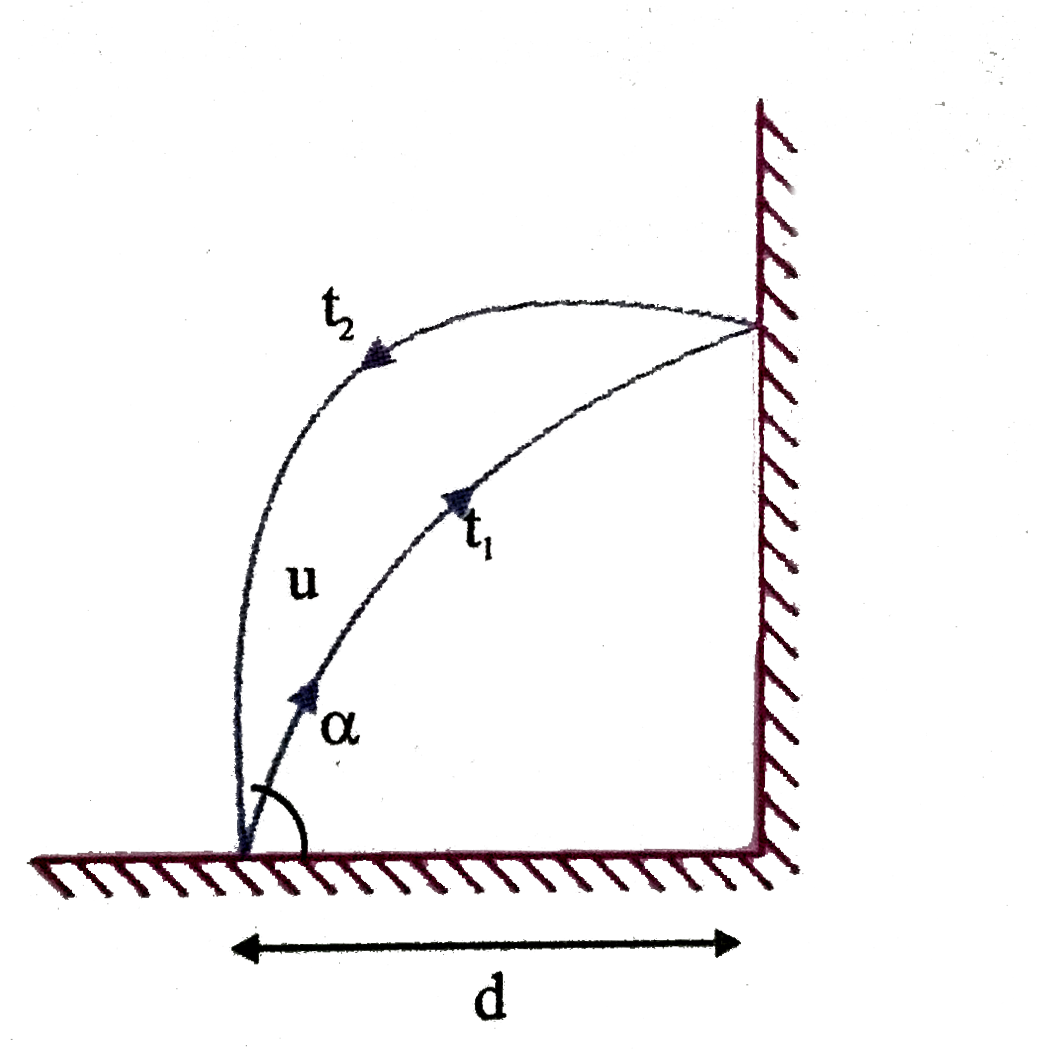
If the line joining the point of projection and the point of impact makes an angle $' θ'$ with the horizontal, then $tan θ$ is
A $e tan α$
B $(1 + e) tan α$
C $\frac{(1 + e)}{tan α}$
D $\frac{tan α}{(1 + e)}$