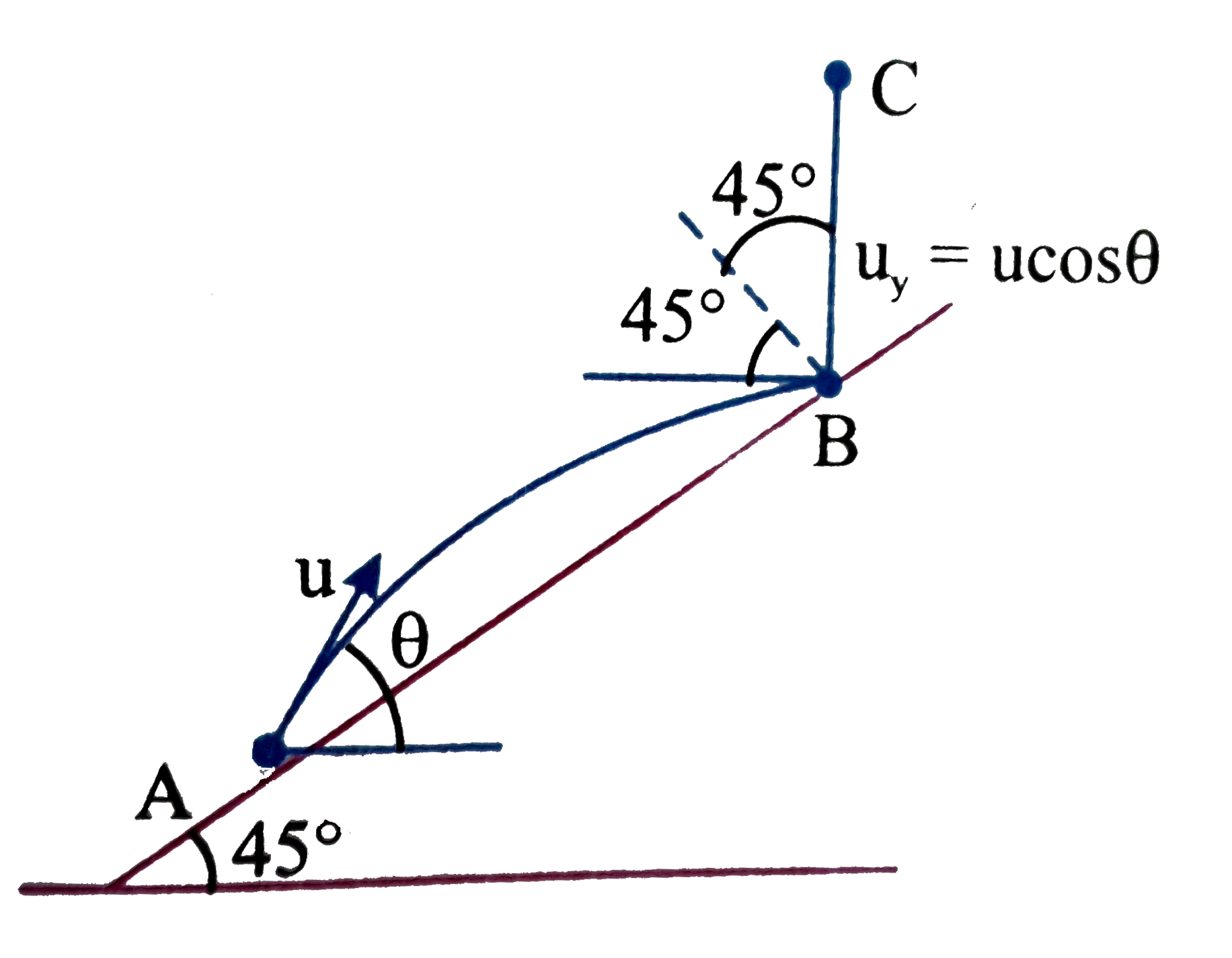
A particle is projected from surface of the inclined plane with speed u and at an angle $θ$ with the horizontal. After some time the particle collides elastically with the smooth fixed inclined plane for the first time and subsequently moves in vertical direction. Starting from projection, find the time taken by the particle to reach maximum height. (Neglect time of collision).

$\frac{2 u \cos θ}{g}$

$\frac{2 u \sin θ}{g}$

$\frac{u (\sin θ + \cos θ)}{g}$

$\frac{2 u}{g}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Updated on:21/07/2023

A particle is projected on an inclined plane with a speed $u$ as shown in (Fig. 5.61). Find the range of the particle on the inclined plane.
.
A $\frac{2 u^{2} \sqrt{3 + 1}}{3 g}$ .
B $\frac{4 u^{2} \sqrt{3 - 1}}{9 g}$ .
C $\frac{2 u^{2} \sqrt{5 - 1}}{8 g}$ .
D $\frac{2 u^{2} \sqrt{3 - 1}}{3 g}$
A particle is projected from ground with speed u and at an angle $θ$ with horizontal. If at maximum height from ground, the speed of particle is $1 / 2$ times of its initial velocity of projection, then find its maximum height attained.
A $\frac{u^{2}}{g}$
B $\frac{2 u^{2}}{g}$
C $\frac{u^{2}}{2 g}$
D $\frac{3 u^{2}}{8 g}$
A particle is projected with a velocity u from the foot of an inclined plane whose inclination to the horizon is $β$ . It strikes. the plane at right angles if
A $tan (α - β) = cot β$
B $2 tan (α - β) = cot β$
C $2 cot (α - β) = cot β$
DNone of these