A projectile is fired with velocity v0 from a gun adjusted for a maximum range.It passes through two points P and Q whose heights above the horizontal are h each.The separation of the two points is
v0g√v20−4gh
v0g√v20+4gh
2v0g√v20−4gh
v0g√v20−gh
The correct Answer is:A
Gun is adjusted for maximum range, therefore α=45∘
y=x−gx2v20orx2−v20gx+v20gh=0
If x1 and x2 are roots of the above equation
x1+x2=v20gandx1x2=v20h
(x1−x2)2=(x1+x2)2−4x1x2
=(v20g)2−4v20gh,x1−x2=v20g√v20−4gh
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level-Vi multiple answer
16 Videos
- MOTION IN A PLANEBOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level-VI Passage answer
18 Videos
- MOTION IN A PLANEBOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Integer
6 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LEVEL-II (H.W)
24 Videos
- MOTION IN A STRAIGHT LINEBOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Level 2 H.W
29 Videos
Similar Questions
A projectile is fired with velocity v0 from a gun adjusted for a maximum range. It passes through two points PandQ whose heights above the horizontal are h each. Show that the separation of the two points is v0g√v20−4gh).
View SolutionA projectile is fired with a velocity u in such a way that its horizontal range is three times the maximum height aatained . Find the value of horizontal range .
View Solution
Knowledge Check
At t=0 a projectile is fired from a point O (taken as origin) on the ground wita speed of 50m/s at an angle of 53∘ with the horizontal. It just passes two points A and B each at height 75m above horizontal.
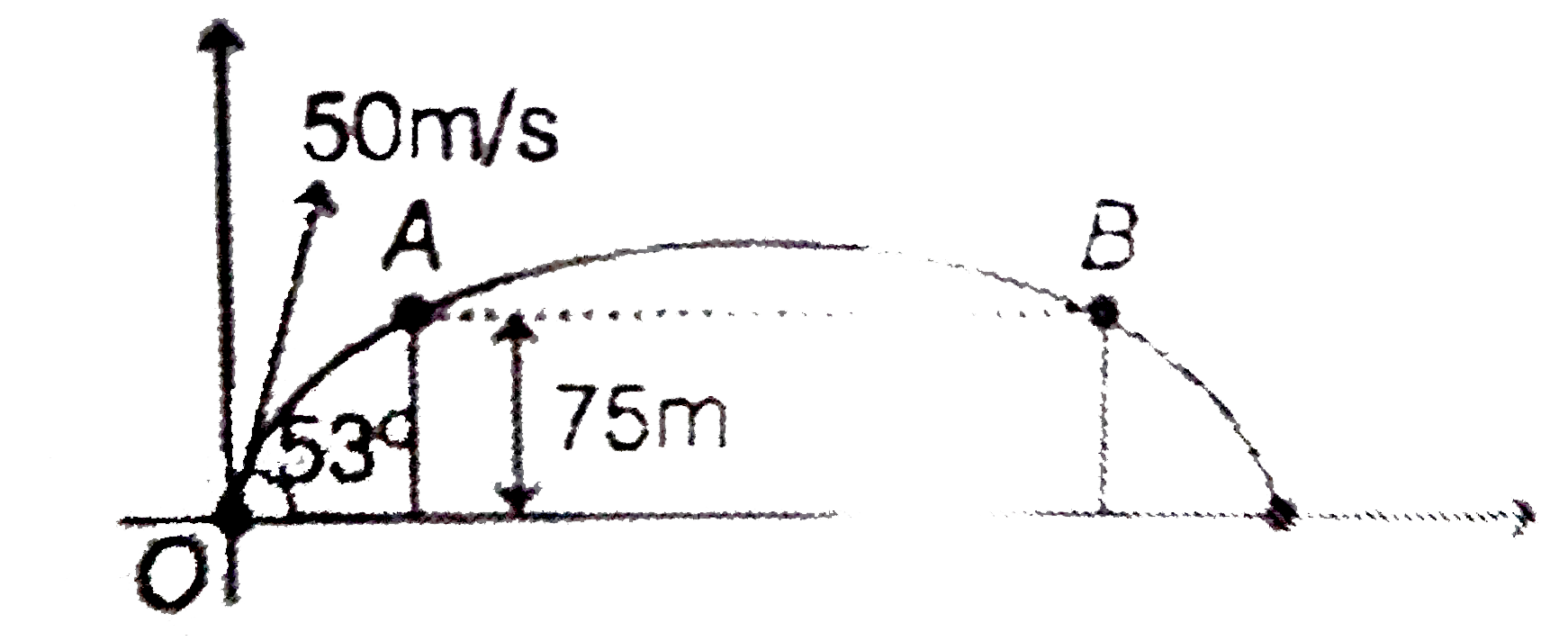
The horizontal separation between the points A and BA30 mB60 mC90 mDNoneAt t=0 a projectile is fired from a point O (taken as origin) on the ground wita speed of 50m/s at an angle of 53∘ with the horizontal. It just passes two points A and B each at height 75m above horizontal.

The horizontal separation between the points A and BA30mB60mC90mDnone of theseA projectile is fired from the origin with a velocity v0 at an angle θ with x-axis. The speed of the projectile at an altitude h is .
Av0cosθB√v20−2ghC√v20sin2θ−2ghDNone of these
two particles are projected upwards with the same initial velocity v0 in two different angles of projection such that their horizontal ranges are the same. The ratio of the heights of their horizontal ranges are the same. The ratio of the heights of their highest point will be
View SolutionTwo projectiles thrown from the same point at angles 60∘and30∘ with the horizontal attain the same height. The ratio of their initial velocities is
View SolutionAt t=0 a projectile is fired from a point O (taken as origin) on the ground wita speed of 50m/s at an angle of 53∘ with the horizontal. It just passes two points A and B each at height 75m above horizontal.
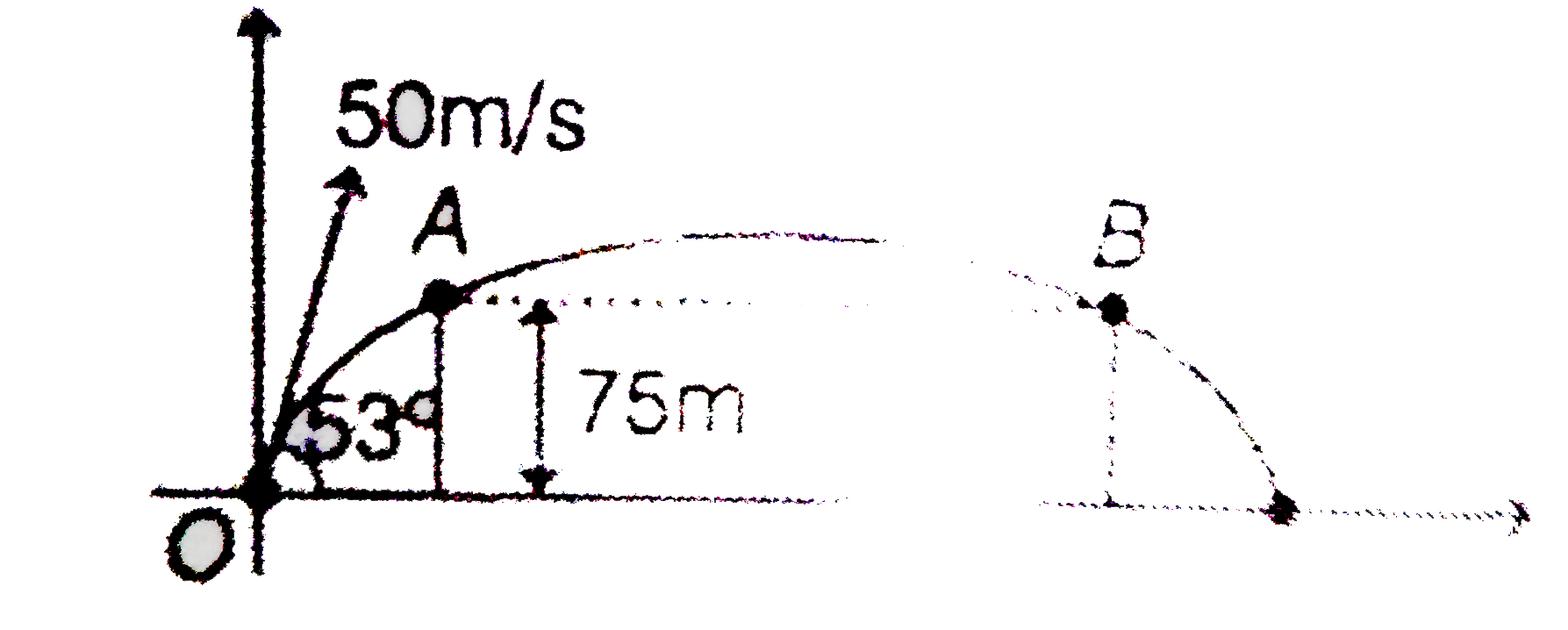
The distance (in metre) of the particle from origin at t=2s
View SolutionAt t=0 a projectile is fired from a point O (taken as origin) on the ground wita speed of 50m/s at an angle of 53∘ with the horizontal. It just passes two points A and B each at height 75m above horizontal.
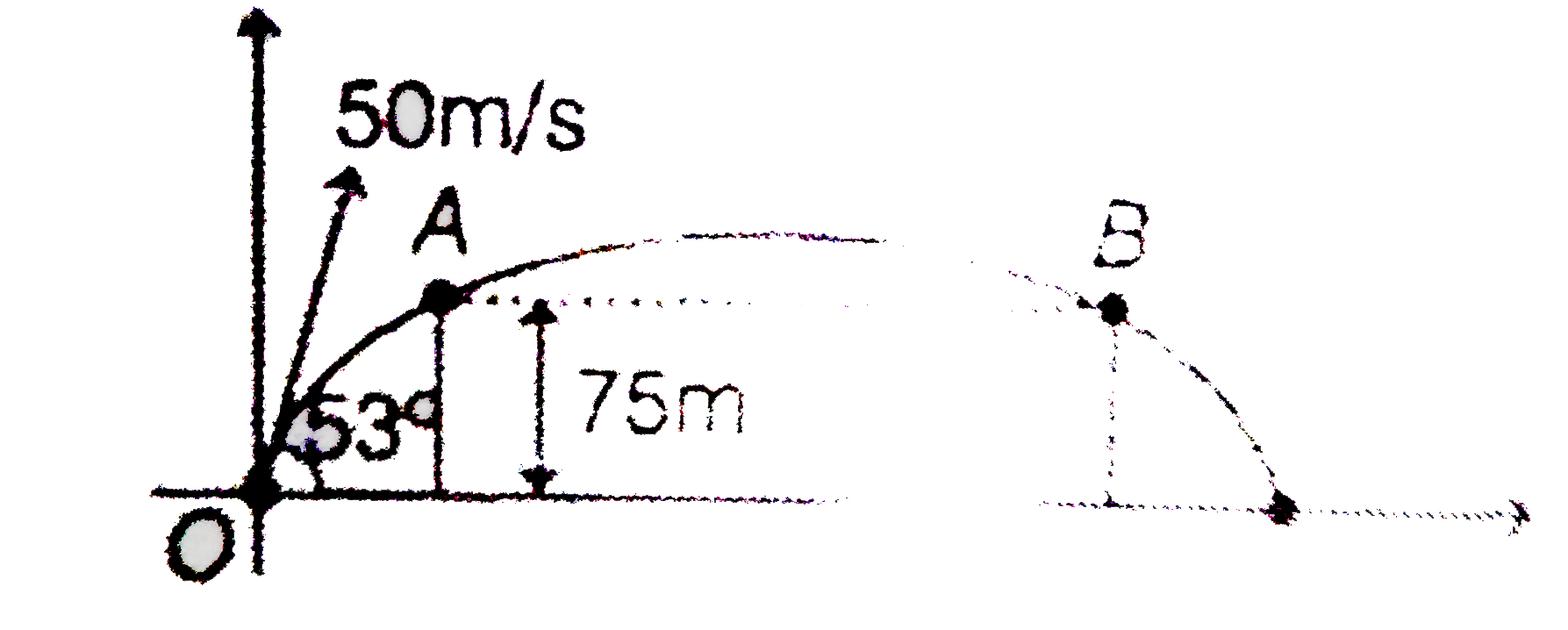
The distance (in metre) of the particle from origin at t=2s
View SolutionA projectile is projected and it takes 9s to reach in the horizontal plane through the point of projection. In its path it passes a point P after 4s. The height of P above the horizontal plane is
View Solution
