A ball projected with a velocity of $10 m / s$ at angle of $30^{\circ}$ with horizontal just clears two vertical poles each of height $1 m$ . Find separation between the poles.

Video Solution

Text Solution

Verified by Experts

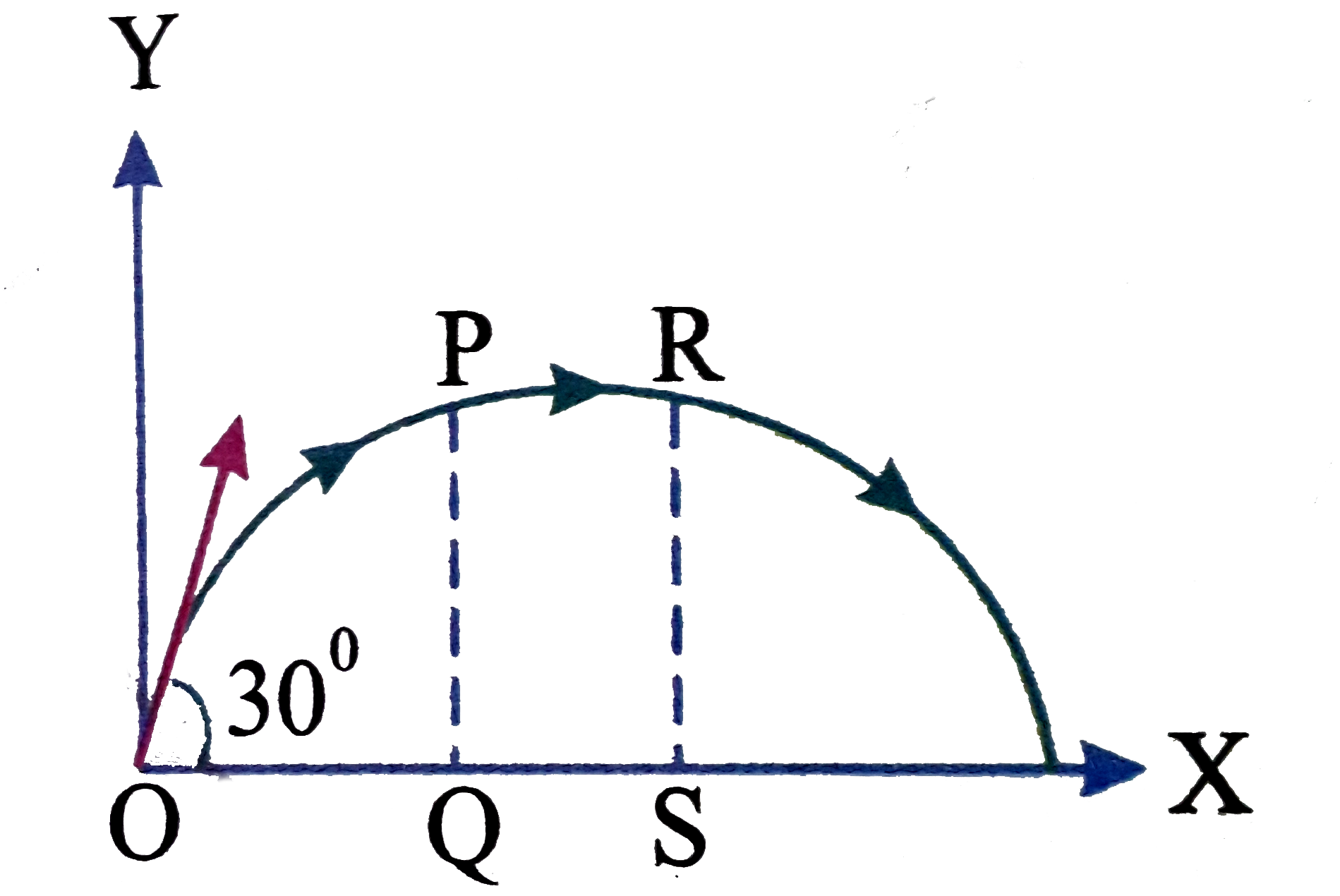
$h = u_{y} t + \frac{1}{2} g t^{2} = (10 {sin 30}^{\circ}) t + \frac{1}{2} (- 10) t^{2}$
$1 = 5 t - 5 t^{2} \Rightarrow t = 0.72 s, 2.76 s$ are the instants at which projectile crosses the poles
$∴$ Separation between poles $= O S - O Q$
$= u cos θ (t_{2} - t_{1})$
$= 10 {cos 30}^{\circ} (2.72 - 0.72) = 17.7 m$

|

Updated on:21/07/2023

Class 11 PHYSICS PROJECTILE MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A particle is projected with a velocity of $25 m / s$ at an angle of $30^{\circ}$ with the horizontal . Calculate
(i) The maximum height ,
(ii) time of flight and
(iii) horizontal range .
A562 m
B286 m
C188 m
D1130 m
Question 2 - Select One
A projectile takes off with an initial velocity of 50m//s at an angle of $37^{\circ}$ with horizontal, It is just able to clear two hurdles of height $25 m$ each, separated from each other by a distance $d$ Calculate $d$ .
A $160 m$
B $50 m$
C $320 m$
D $40 m$
Question 3 - Select One
A particle is projected with velocity of $10 \frac{m}{s}$ at an angle of 15° with horizontal.The horizontal range will be $(g = 10 \frac{m}{s^{2}})$
A10m
B5m
C2.5m
D1m

NARAYNA-MOTION IN A PLANE-Level-II(H.W)

Home
Ask Doubt
Profile