A and B are two pegs separated by 13cm.A body of 169kgwt is suspended by thread of 17cm connecting to A&B, such that the two segments of strings are perpendicular.Then tensions in shorter and longer parts of string are
100kgwt,69kgwt
65kgwt,156kgwt
156kgwt,65kgwt
69kgwt,100kgwt
The correct Answer is:B
To solve the problem of finding the tensions in the shorter and longer parts of the string, we can follow these steps:
Step 1: Understand the Setup
We have two pegs, A and B, separated by a distance of 13 cm. A body weighing 169 kg (which is equivalent to 169 kgwt) is suspended by a thread of total length 17 cm. The segments of the string connecting to the pegs are perpendicular to each other.
Step 2: Define Variables
Let:
- T1 = Tension in the shorter segment of the string
- T2 = Tension in the longer segment of the string
- x = Length of the shorter segment of the string
- 17−x = Length of the longer segment of the string
Step 3: Apply Geometry
Since the segments of the string are perpendicular, we can use the Pythagorean theorem:
x2+(17−x)2=132
Expanding this gives:
x2+(172−34x+x2)=169
2x2−34x+289−169=0
2x2−34x+120=0
Step 4: Solve the Quadratic Equation
Using the quadratic formula x=−b±√b2−4ac2a:
- Here, a=2, b=−34, and c=120.
x=34±√(−34)2−4⋅2⋅1202⋅2
x=34±√1156−9604
x=34±√1964
x=34±144
Calculating the two possible values:
1. x=484=12 cm
2. x=204=5 cm
Step 5: Assign Values
- The shorter segment x=5 cm
- The longer segment 17−x=12 cm
Step 6: Find Angles
Using the definitions of cosine:
cosθ1=513,cosθ2=1213
Using the definitions of sine:
sinθ1=1213,sinθ2=513
Step 7: Set Up Equations
From the balance of horizontal components:
T1cosθ1=T2cosθ2
Substituting the values:
T1⋅513=T2⋅1213
This simplifies to:
T1=125T2
From the balance of vertical components:
T1sinθ1+T2sinθ2=169
Substituting the values:
T1⋅1213+T2⋅513=169
Multiplying through by 13:
12T1+5T2=169⋅13
12T1+5T2=2197
Step 8: Substitute for T1
Substituting T1=125T2 into the vertical equation:
12(125T2)+5T2=2197
1445T2+5T2=2197
Multiplying through by 5 to eliminate the fraction:
144T2+25T2=10985
169T2=10985
T2=10985169=65 kgwt
Step 9: Find T1
Using T1=125T2:
T1=125⋅65=156 kgwt
Final Answer
- Tension in the shorter part of the string T1=156 kgwt
- Tension in the longer part of the string T2=65 kgwt
---
We have two pegs, A and B, separated by a distance of 13 cm. A body weighing 169 kg (which is equivalent to 169 kgwt) is suspended by a thread of total length 17 cm. The segments of the string connecting to the pegs are perpendicular to each other.
Let:
- T1 = Tension in the shorter segment of the string
- T2 = Tension in the longer segment of the string
- x = Length of the shorter segment of the string
- 17−x = Length of the longer segment of the string
Since the segments of the string are perpendicular, we can use the Pythagorean theorem:
x2+(17−x)2=132
Expanding this gives:
x2+(172−34x+x2)=169
2x2−34x+289−169=0
2x2−34x+120=0
Using the quadratic formula x=−b±√b2−4ac2a:
- Here, a=2, b=−34, and c=120.
x=34±√(−34)2−4⋅2⋅1202⋅2
x=34±√1156−9604
x=34±√1964
x=34±144
Calculating the two possible values:
1. x=484=12 cm
2. x=204=5 cm
- The shorter segment x=5 cm
- The longer segment 17−x=12 cm
Using the definitions of cosine:
cosθ1=513,cosθ2=1213
Using the definitions of sine:
sinθ1=1213,sinθ2=513
From the balance of horizontal components:
T1cosθ1=T2cosθ2
Substituting the values:
T1⋅513=T2⋅1213
This simplifies to:
T1=125T2
T1sinθ1+T2sinθ2=169
Substituting the values:
T1⋅1213+T2⋅513=169
Multiplying through by 13:
12T1+5T2=169⋅13
12T1+5T2=2197
Substituting T1=125T2 into the vertical equation:
12(125T2)+5T2=2197
1445T2+5T2=2197
Multiplying through by 5 to eliminate the fraction:
144T2+25T2=10985
169T2=10985
T2=10985169=65 kgwt
Using T1=125T2:
T1=125⋅65=156 kgwt
- Tension in the shorter part of the string T1=156 kgwt
- Tension in the longer part of the string T2=65 kgwt
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - NARAYNACHAPTER - MOTION IN A PLANEEXERCISE - Level-I (H.W)
41 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NARAYNACHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - LEVEL-II (H.W)
24 Videos
- MOTION IN A STRAIGHT LINEBOOK - NARAYNACHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Level 2 H.W
29 Videos
Similar Questions
Draw a line segment of length 6cm. Construct its perpendicular bisector. Measure the two parts of theline segment.
View SolutionA body of mass 50 kg, suspended by two strings of lengths 30 cm and 40 cm fastend to two points in the same horizontal line 50 cm apart, is in equilibrium. Find the tension (in Newtons) in each string.
View Solution
Knowledge Check
A body of 6⋅5 kg is suspended by two strings of lengths 5 and 12 metres attached to two points in the same horizontal line whose distance apart is 13 metre. The tension of the strings in kg wt. are
A3,5B2⋅5,6C4,5D3.4A uniform horizontal metre scale of mass m is suspended by two vertical strings attached to its two ends. A body of mass 2m is placed on the 75 cm mark. The tensions in the two strings are in the ratio is
A1:2B1:3C2:3D3:4A uniform horizontal meter scale of mass m is suspended by two vertical strings attached to its two ends. A block of mass 3m is placed on the 60cm mark. The tensions in the two strings are in the ratio
A17:19B19:21C17:23D19:23
A body of mass mis suspended by two strings making angles αandβ with the horizontal. Find the tensions in the strings.
View SolutionA blolck D weighing 300kg is suspended by means of two cords A and B as shown in the figure. W is a vertical wall and R a horizontal rigid beam. The tension in the string A in kg is :
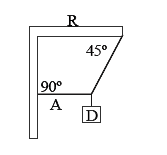
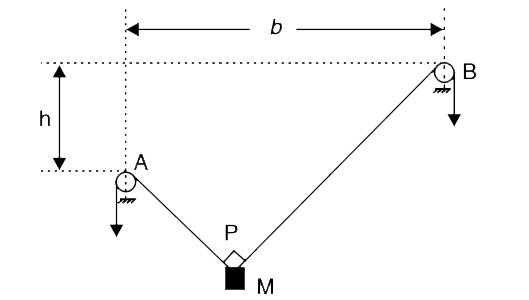
View SolutionTwo small pegs (A and B) are at horizontal and vertical separation b and h respectively. A small block of mass M is suspended with the help of two light strings passing over A and B as shown in fig. The two string are always kept at right angles (i.e., <APB=90∘). Find the minimum possible gravitation potential energy of the mass assuming the reference level at location of peg A. [Hint: the potential energy is minimum when the block is at its lowest position]
View SolutionA cylinder of mass m is suspended through two strings wrapped around it as shwon in figure . Find a. the tension T in the string and b. the speed o the cylinder as it falls through a distance h.

View SolutionA uniform horizontal meter scale of mass m is susopended by two certical string attached to its two ends. A body of mass 2m is place on the 75−cm mark. The tensions in the two strings are in the ratio
View Solution