A boat is moving with a velocity $v_{b w} = 5 k m / h r$ relative to water. At time $t = 0$ .the boat passes through a piece of cork floating in water while moving down stream.If it turns back at time $t_{1} = 30 min$ .
a) when the boat meet the cork again?
b) The distance travelled by the boat during this time.

Video Solution

Text Solution

Verified by Experts

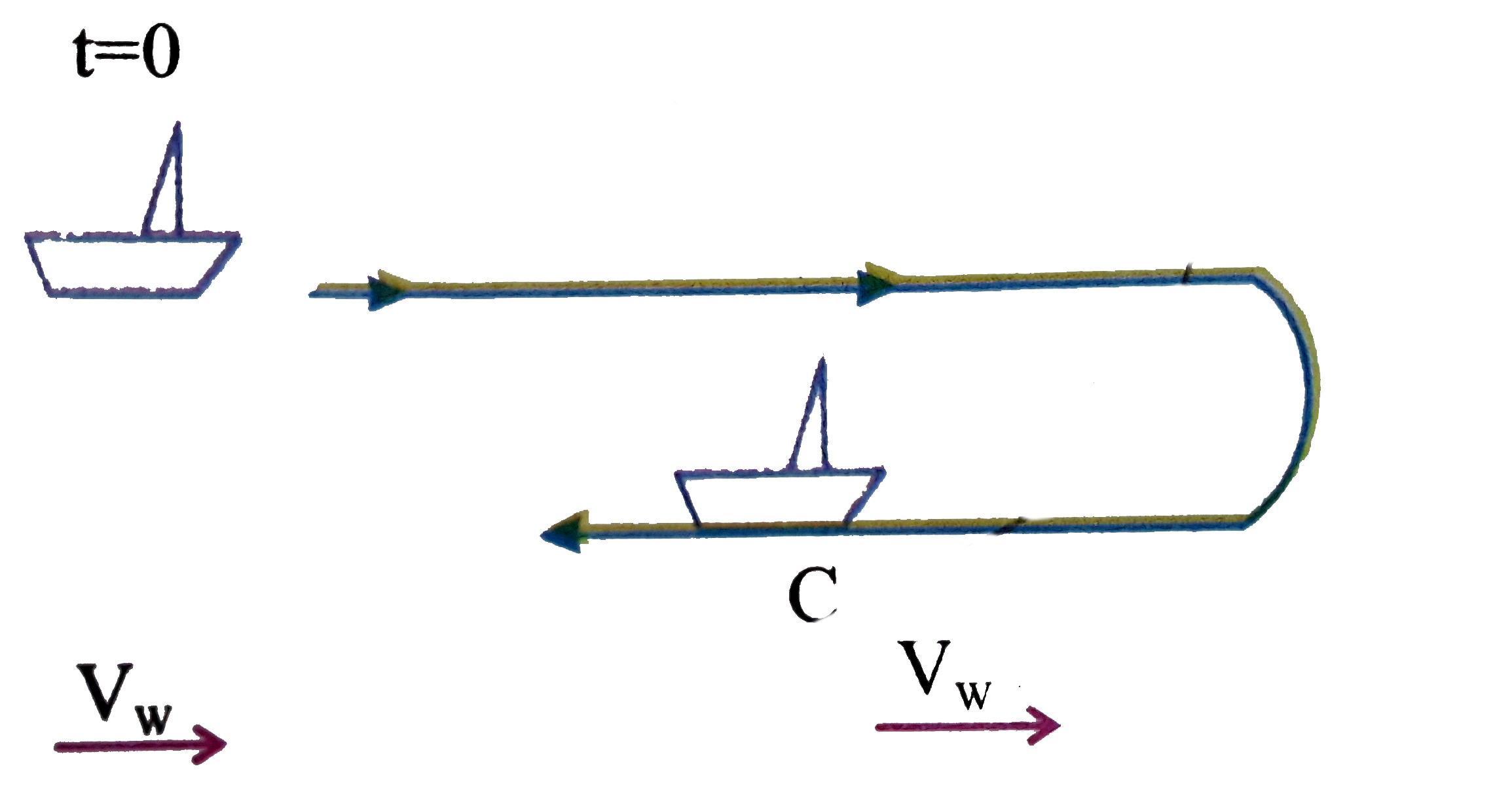
Let $A B = d$ is the distance travelled by boat along down stream in $t_{1}$ sec and it returns back and it meets the cork at point $C$ after $t_{2}$ sec.
$∴$ Let $A C = x$ is the distance travelled by the cork during $(t_{1} + t_{2})$ sec.
$d = (V_{B} + V_{W}) t_{1}$ ....(1)
$d - x = (V_{B} - V_{W}) t_{2}$ ....(2)
$x = V_{W} (t_{1} + t_{2})$ ....(3)
Substitute (1) and (3) in (2) we get $t_{1} = t_{2}$
$∴$ The boat meets the cork again after $T = 2 t_{1} = 60 min$ and the distance $(A B + B C)$ travelled by the boat before meets the cork is
$D = 2 d - x$
$D = 2 (V_{B} + V_{W}) t_{1} - V_{w} 2 t_{1}$
$D = 2 V_{B} t^{1} + 2 V_{w} t_{1} - 2 V_{w} t_{1}$
$D = 2 V_{B} t_{1} = 2 \times 5 \times \frac{30}{60} = 5 k m$

Updated on:21/07/2023

A boat takes $4 h r s$ to travel certain distance in a river in down stream and it takes $6 h r s$ to travel the same distance in upstream. Then the time taken by the boat to travel the same distance in still water is
A $4.8 h r s$
B $9.8 h r s$
C $24 h r s$
D $10 h r s$
A boat can be rowed in still water at a speed u. The boat is moving downstream in a river in which water flows at a speed v. There is raft floating in water and therefore moving along with water at speed v. Let the boat overtakes the raft at the moment t = 0.
The distance between the boat and raft at a later instant of time t is
A $(u + v) t$
B $u t$
C $v t$
D $(u - v) t$
A boat can travel with a speed of 30 km/hr in still water. If the speed of the stream is 6 km/hr, find the time taken by the boat to go 108 km downstream.
A2 hrs
B5 hrs
C3 hrs
D4 hrs