A rod of length L lies along the x-axis with its left end at the origin. It has a non-uniform charge density λ=αx, where a is a positive constant.
(a) What are the units of α?
(b) Calculate the electric potential at point A where x=−d .
Charge per unit length λ=QL
Taking O as origin , take an element of small length dx at distance x from the origin.
Charge on element dq=λdx
Small potential at P due to dq
dV=14π∈0.dq(2L−x)=Q4π∈0Ldx(2L−x)
VP=Q4π∈0L∫L0dx(2L−x)
I=∫L0dx(2L−x)=|loge(2L−x)|L0−1
=−[loge(2L−L)−loge(2L−0)]
=−loge(L2L)=−loge(12)=loge2
VP=14π∈0Qloge2L
Small electric field at P due to dq
dE=14π∈0.dq(2L−x)2=Q4π∈0L.dx(2L−x)2
EP=Q4π∈0L∫L0dx(2L−x)2
I=∫L0dx(2L−x)2=∫L0(2L−x)−2dx
=∣∣(2L−x)−1∣∣L0(−1)(−1)=∣∣∣1(2L−x)∣∣∣L0
=12L−L−12L−0=1L−12L=12L)
EP=14π∈0.Q2L2

Topper's Solved these Questions
Similar Questions
A continuous line of charge of length 3d lies along the x-axis, extending from x + d to x + 4d, The line carries a uniform linear charge density lambd . In terms of d,λ and any necessary physical constant find the magnitude of the electric field at the origin.
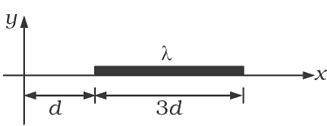
View SolutionA straight rod of length L has one of its end at the origin and the other at X=L. If the mass per unit length of the rod is given by Ax where A is constant, where is its centre of mass?
View Solution
Knowledge Check
A rod of length 'l' is placed along x-axis. One of its ends is at the origin. The rod has a non-uniform charge density λ= a, a being a positive constant. Electric potential at P as shown in the figure is -
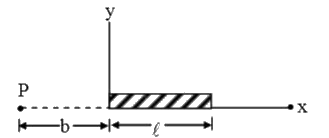 Aa4πε0ln(b+lb)Ba4πε0lnlbCa4πε0lnblDzero
Aa4πε0ln(b+lb)Ba4πε0lnlbCa4πε0lnblDzeroA rod of length l is placed along x - axis. One of its ends is at the origin. The rod has a non - uniform charge density λ=ax, a being a positive constant. The electric potential at the point P (origin) as shown in the figure is
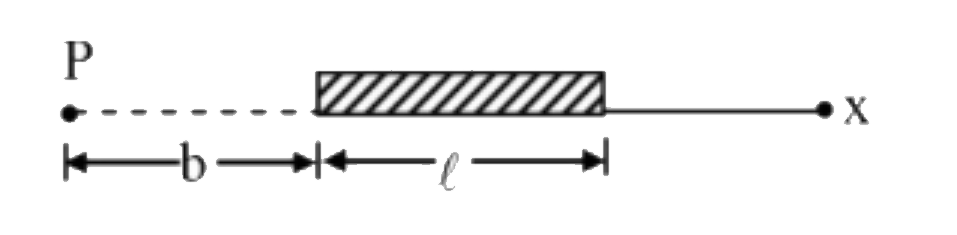 AV=a4πε0(lb(b+l))BV=a4πε0(bl(b+l))CV=a4πε0(bl)DV=a4πε0(lb)
AV=a4πε0(lb(b+l))BV=a4πε0(bl(b+l))CV=a4πε0(bl)DV=a4πε0(lb)A rod lies along the x-axis with one end at the origin and the other at x→∞. It carries a uniform charge λ C/m. The electric field at the point x = -a on the axis will be
A→E=λ4πε0a(−ˆi)B→E=λ4πε0a(ˆi)C→E=λ2πε0a(−ˆi)DE=λ2πε0a(ˆi)
A continuous line of charge oflength 3d lies along the x-axis, extending from x+d tox+4d . the line carries a uniform linear charge density λ.

In terms of d,λ and any necessary physical constants, find the magnitude of the electric field at the origin:
View SolutionA non-uniform thin rod of length L is palced along X-axis so that one of its ends is at the origin. The linear mass density of rod is λ=λ0x. The centre of mass of rod divides the length of the rod in the ratio:
View SolutionA rod lies along the X-axis with one end at the origin and the other at x→∞. It carries a uniform charge λCm−1. The electric field at the point x=−a on the axis will be
View SolutionA rod length L and mass M is placed along the x-axis with one end at the origin, as shown in the figure above. The rod has linear mass density λ=2ML2x, where x is the distance from the origin. Which of the following gives the x-coordinate of the rod's center of mass?

View SolutionA non–uniform thin rod of length L is placed along x-axis as such its one of ends at the origin. The linear mass density of rod is λ=λ0x. The distance of centre of mass of rod from the origin is :
View Solution