A non-uniform thin rod of length L is palced along X-axis so that one of its ends is at the origin. The linear mass density of rod is λ=λ0x. The centre of mass of rod divides the length of the rod in the ratio:
The correct Answer is:(2/1)
As shown in Fig. mass of small element of length dx is
dm=λdx=λ0xdx
∴xcm=∫L0xdm∫dm=∫L0x(λ0xdx)∫L0λ0xdx
xcm=[x3/3]L0[x2/2]L0=L3/3L2/2=2L3
If x1=2L3,x2=L−2L3=L3
x1x2=2L/3L/3=21

Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:Assertion- Reason Type questions
Explore 20 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:Multiple Choice Questions Comprehension 2
Explore 1 Video
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Problem For Practice(a)
Explore 25 Videos
- THERMODYNAMICSBook:PRADEEPChapter:THERMODYNAMICSExercise:Assertion- Reason Type Questions
Explore 19 Videos
Similar Questions
A rod of length L is placed along the x-axis between x=0 and x=L. The linear mass density is λ such that λ=a+bx. Find the mass of the rod.
View SolutionA rod of length l is pivoted about an end . Find the moment of inertia of the rod about this axis if the linear mass density of rod varies as ρ=ax2+b kg/m
View Solution
Knowledge Check
A non–uniform thin rod of length L is placed along x-axis as such its one of ends at the origin. The linear mass density of rod is λ=λ0x. The distance of centre of mass of rod from the origin is :
AL/2B2L/3CL/4DL/5A rod of length 'l' is placed along x-axis. One of its ends is at the origin. The rod has a non-uniform charge density λ= a, a being a positive constant. Electric potential at P as shown in the figure is -
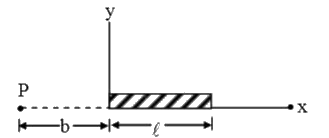 Aa4πε0ln(b+lb)Ba4πε0lnlbCa4πε0lnblDzero
Aa4πε0ln(b+lb)Ba4πε0lnlbCa4πε0lnblDzeroFind centre of mass of given rod of linear mass density λ=(a+b(xl)2) , x is distance from one of its end. Length of the rod is l.
A3l4(3a+b2a+b)B3l4(2a+b3a+b)Cl4(2a+b3a+b)Dl(2a+b3a+b)
A thin rod of length 6m is lying along the x-axis with its ends at x=0 and x=6m. It linear density (mass/length) varies with x as kx4. Find the position of centre of mass of rod in meters.
View SolutionIf linear density of a rod of length 3m varies as λ=2+x, them the position of the centre of gravity of the rod is
View SolutionA thin rod of length 6 m is lying along the x-axis with its ends at x=0 and x=6m. Its linear density *mass/length ) varies with x as kx4. Find the position of centre of mass of rod in meters.
View SolutionA rod of length l is placed along x - axis. One of its ends is at the origin. The rod has a non - uniform charge density λ=ax, a being a positive constant. The electric potential at the point P (origin) as shown in the figure is
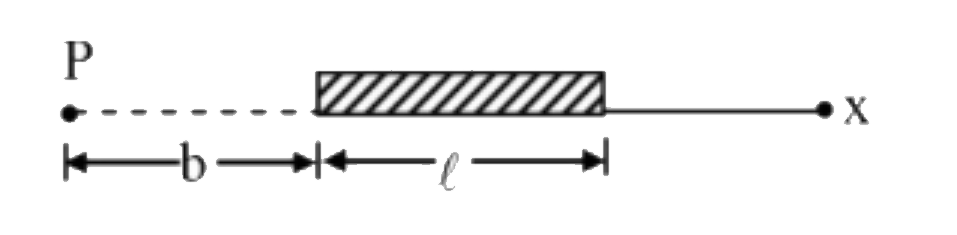
View SolutionThree thin rods, each of length 2 m and mass 3 kg are placed along x, y and z axes, such that one end of each rod is at the origin. The moment of inertia of this system about the x axis is
View Solution

