A small transparent slab (μ=1.5) is placed along AS2 as shown.

AC=CO=D,S1C=S2S=d<<D
The distance of first minima above O is
3D√43
D√247
3D√247
5D√247
The correct Answer is:C
Path difference =2dsinθ+(μ−1)l
∴ For principal maxima,
2dsinθ+0.5l=0
sinθ0=−l4d=−116 , (⟨'l=d4)
∴OP=Dtanθ0≈−D16
for the first minima :
∴2dsinθ+0.5l=±λ2
The first minima the positive side is at distance
Dtanθ+=D3√162−32 above O.
In the −ve side, the distance will be
Dtanθ−=D5√162−52 below O.
Topper's Solved these Questions
- WAVE OPTICSBOOK - NARAYNACHAPTER - WAVE OPTICSEXERCISE - LEVEL - V
37 Videos
- WAVE OPTICSBOOK - NARAYNACHAPTER - WAVE OPTICSEXERCISE - LEVEL - VI
40 Videos
- WAVE OPTICSBOOK - NARAYNACHAPTER - WAVE OPTICSEXERCISE - LEVEL - III
30 Videos
- SEMICONDUCTOR ELECTRONICSBOOK - NARAYNACHAPTER - SEMICONDUCTOR ELECTRONICSEXERCISE - ADDITIONAL EXERCISE (ASSERTION AND REASON TYPE QUESTIONS :)
19 Videos
Similar Questions
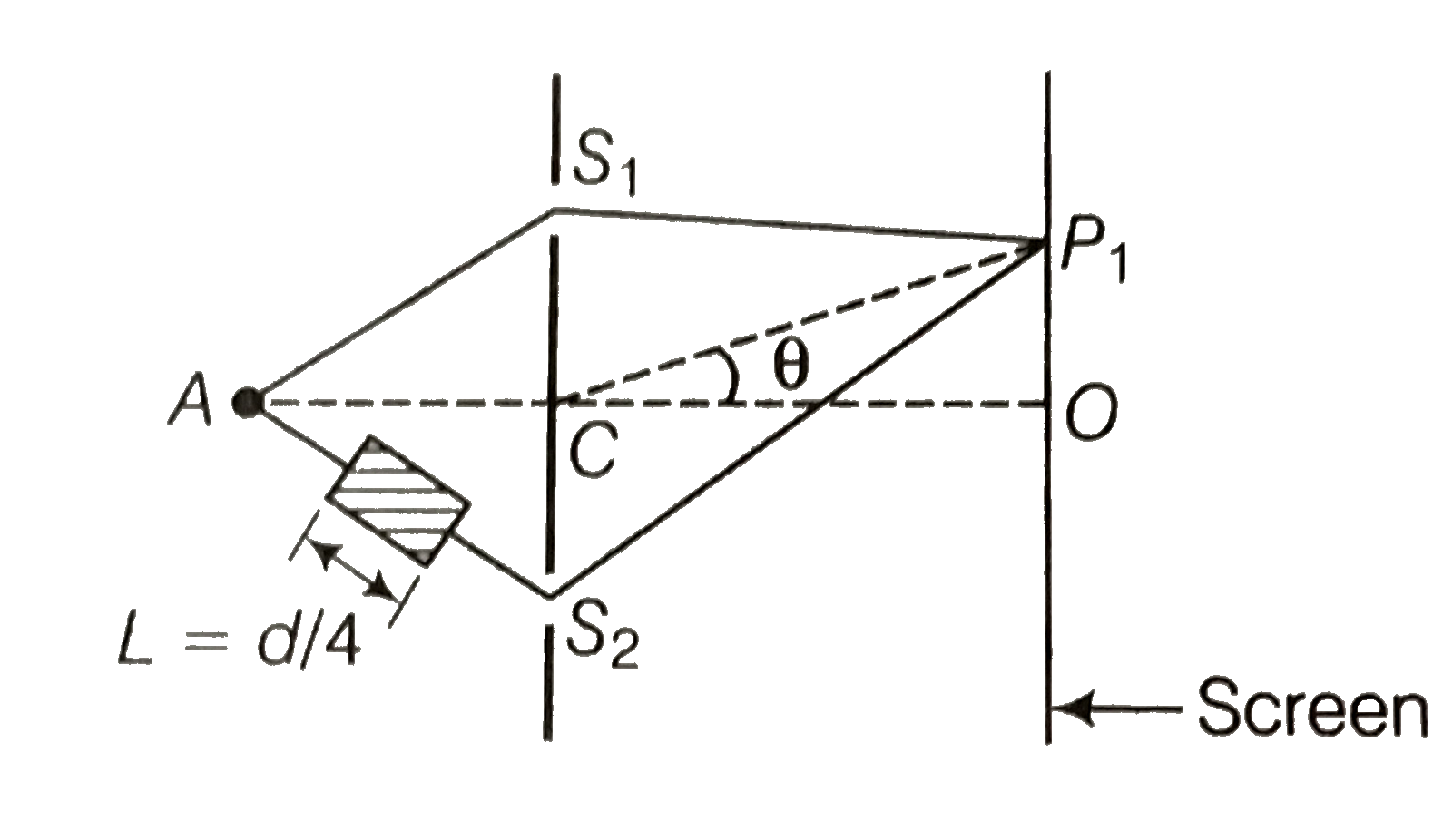
A small transparent slab containing material of μ=1.5 is placed along AS2(figure). What will be the distance from O of the principle maxima and of the first minima on either side of the principal maxima obtained in the absence of the glass slab ?
View SolutionMonochromatic light of wavelength λ passes through a very narrow slit S and then strikes a screen placed at a distance D = 1m in which there are two parallel slits S1 and S2 as shown. Slit S1 is directly in line with S while S2 is displaced a distance d to one side. The light is detected at point P on a second screen, equidistant from S1 and S2 When either slit S1 or S2 is open equal light intensities I are measured at point P. When both slits are open, the intensity is three times as large i.e. 3I. If the minimum possible wavelength is Nd2, then find the value of N(d<<D)

View Solution
Knowledge Check
A small transparent slab (μ=1.5) is placed along AS2 as shown.

AC=CO=D,S1C=S2S=d<<D
The distance of first minima below the point O isAD√231B3D√231C2D√231D5D√231A small transparent slab (μ=1.5) is placed along AS2 as shown.

AC=CO=D,S1C=S2S=d<<D
The distance of princpal maxima front 'O' isAD4BD16CD8DDTwo ideal slits S1 and S2 are at a distance d apart, and illuninated by light of wavelength λ passing through an ideal source slit S placed on the line through S2 as shown. The distance between the planes of slits and the source slit is D.A screen is held at a distance D from the plane of the slits. The minimum value of d for which there is darkness at O is (d<<D)
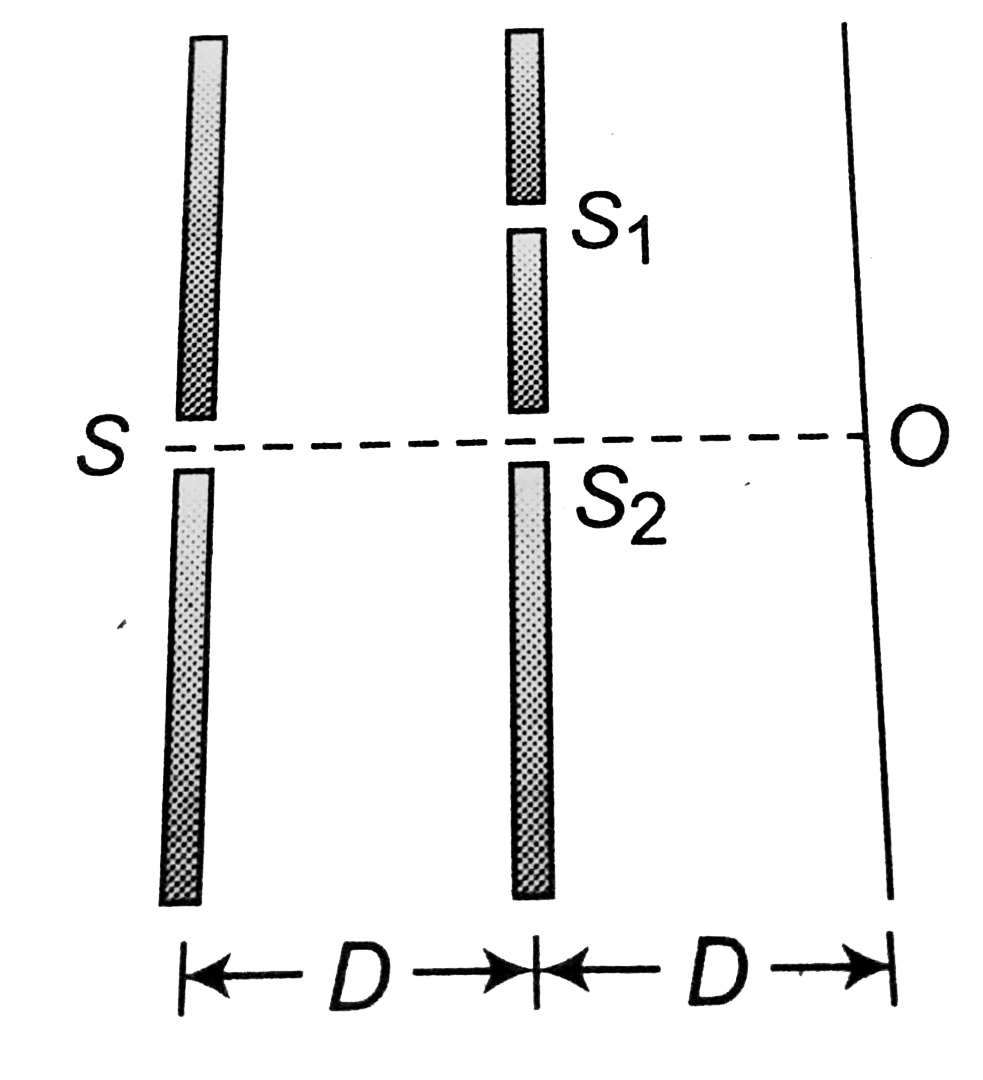 A√3λD2B√λDC√λD2D√3λD
A√3λD2B√λDC√λD2D√3λD
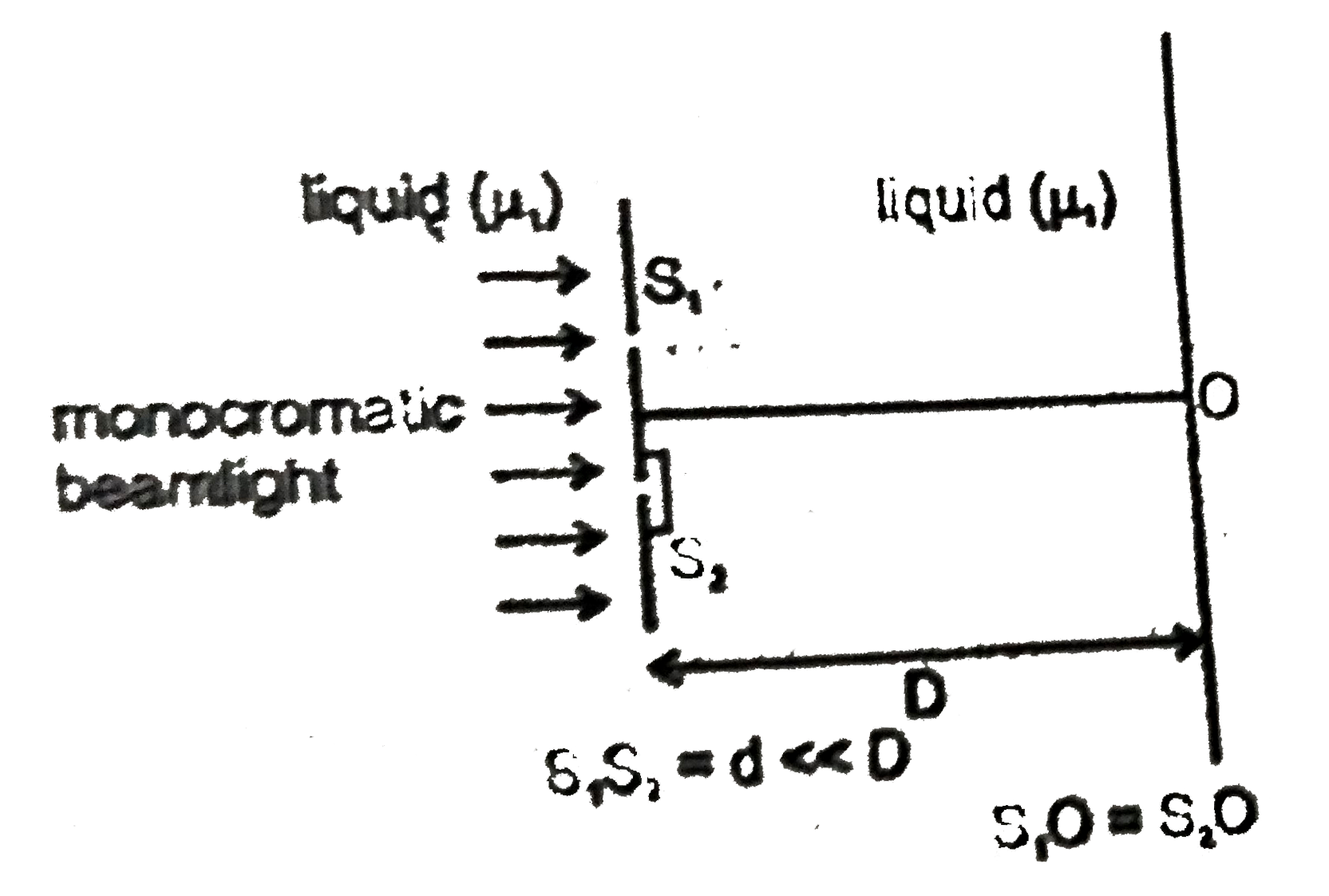
Young's double slit experiment is conducted in a liquid of refractive index μ1 as shown in figure. A thin transparent slab of refractive index μ2 is placed in front of the slit s2. The magnitude of optical path difference at 'O' is
View SolutionIn YDSE arangement shown in figure, fringes are seen on screen using monochromatic source S having wavelength 3000∘Δ (in air). S1 and S2 are two slits separate by d=1mm and D=1m . Left of slits S1andS2 medium of refractive index μ1=2 is presernt refractive index μ2=32 is present. A thin slab of thickness 't' is placed in front of S1 . The refractive index of slab μ3 varies with distance from its starting face as shown in figure.

If the thickness of the slab is selected 1μm , then the position of the central maxima will be (y - coordinate)
View SolutionMicrowave ocillators S1andS2 are used to show interference of electromagnetic waves on a screen which in parallel to S1S2 and 2 m away from S1S2 . If S1S2=20 cm and λ=4cm, then the distance between the successive maxima and minima will be
View SolutionIn YDSE arrangement as shown in figure, fringes are seen on screen using monochromatic source S having wavelength 3000 Å (in air). S1and S2 are two slits seperated by d = 1 mm and D = 1m. Left of slits S1 and S2 medium of refractive index n1=2 is present and to the right of S1 and S2 medium of n2=32, is present. A thin slab of thickness 't' is placed in front of S1 . The refractive index of n3 of the slab varies with distance from it's starting face as shown in figure.

In order to get central maxima at the centre of screen, the thickness of slab required is :
View SolutionConsider the situation shown in fig. The two slits S1 and S2 placed symmetrically around the central line are illuminated by monochromatic light of wavelength λ. The separation between the slit is d. The ligth transmitted by the slits falls on a screen S0 placed at a distance D form the slits. The slit S3 is at the central line and the slit S4 is at a distance z from S3 Another screen Sc is placed a further distance D away from Sc Find the ratio of the maximum to minimum intensity observed on Sc
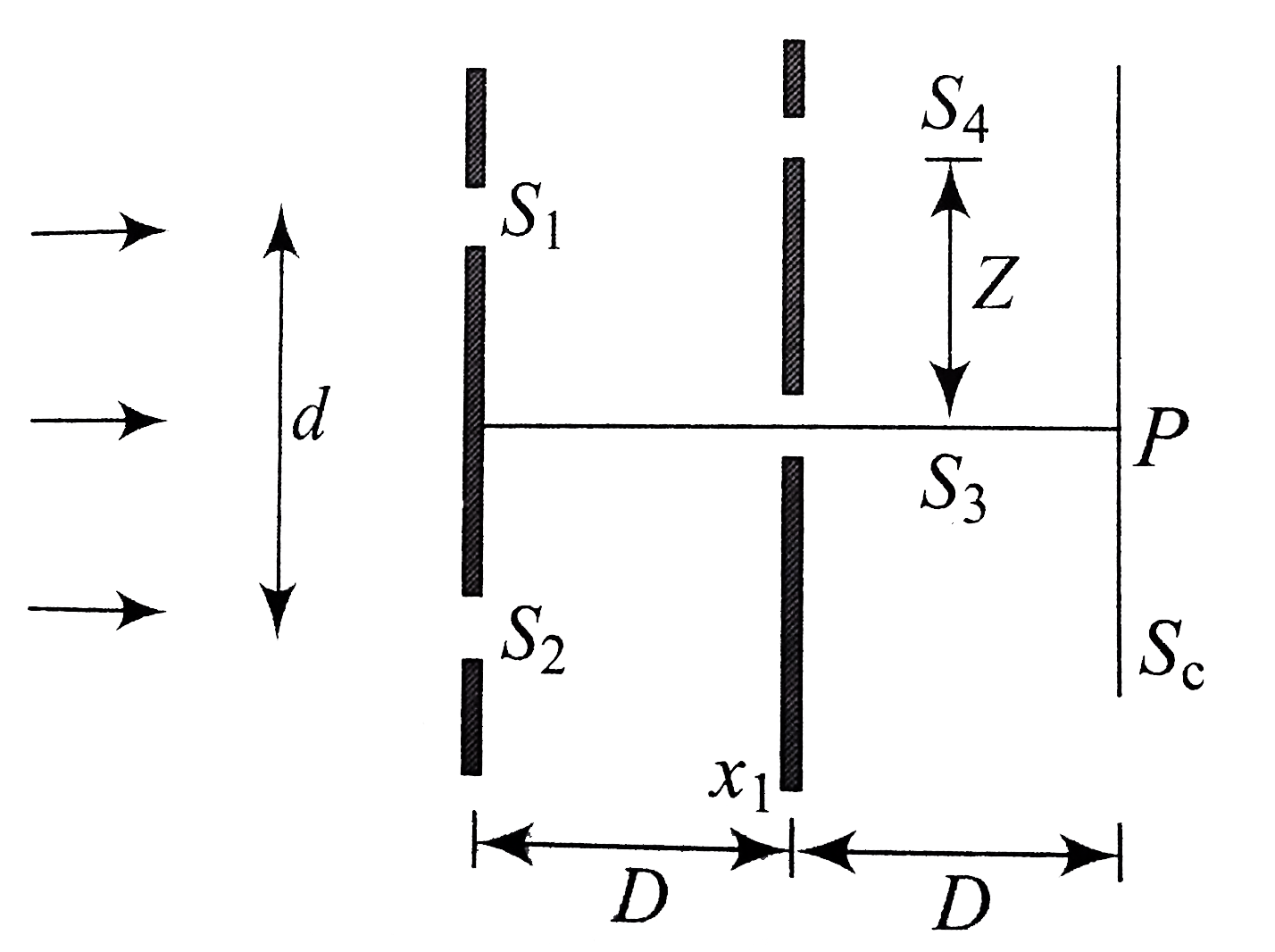
If z=λD2d
View Solution
