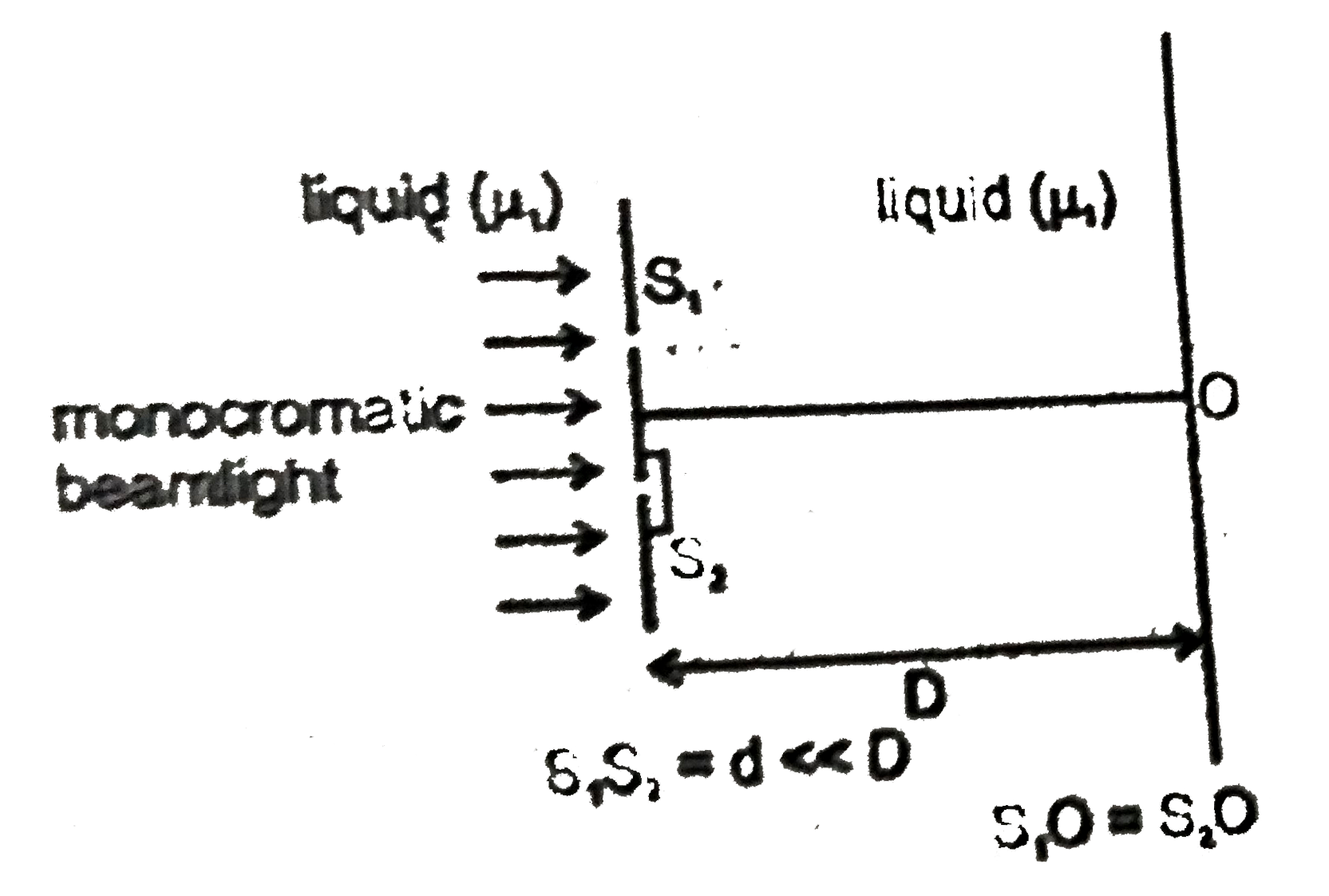
Young's double slit experiment is conducted in a liquid of refractive index $μ_{1}$ as shown in figure. A thin transparent slab of refractive index $μ_{2}$ is placed in front of the slit $s_{2}$ . The magnitude of optical path difference at 'O' is
$Young's double slit experiment is conducted in a liquid of refractive index mu1 as shown in figure. A thin transparent slab of refractive index mu2 is placed in front of the slit s2. The magnitude of optical path difference at 'O' is$

$∣ ∣ ∣ (\frac{μ_{2}}{μ_{1}} - 1) t ∣ ∣ ∣$

$∣ ∣ ∣ (\frac{μ_{1}}{μ_{2}} - 1) t ∣ ∣ ∣$

$| (μ_{2} - μ_{1}) t |$

$| (μ_{2} - 1) t |$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Updated on:21/07/2023

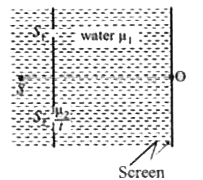
A YDSE is conducted in water $(μ_{1})$ as shown in figure. A glass plate of thickness t and refractive index $μ_{2}$ is placed in the path of $S_{2}$ . The optical path difference at O is

A $(μ_{2} - 1) t$
B $(μ_{1} - 1) t$
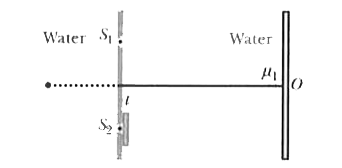
C $(\frac{μ_{2}}{μ_{1}} - 1) t$
D $(μ_{2} - μ_{1}) t$
A Young's double-slit experiment is conducted in water $(n_{1})$ as shown in the following figure, and a glass plate of thickness t and refractive index $n_{2}$ is placed in the path of $S_{2}$ . Wavelength of light in water is $λ$ . Find the magnitude of the phase difference between waves coming from $S_{1}$ and $S_{2}$ at O.

A $∣ ∣ ∣ (\frac{n_{2}}{n_{1}} - 1) t ∣ ∣ ∣ \frac{2 π}{λ}$
B $∣ ∣ ∣ (\frac{n_{2}}{n_{1}} - 1) t ∣ ∣ ∣ \frac{2 π}{λ}$
C $| (n_{2} - n_{1}) t | \frac{2 π}{λ}$
D $| (n_{2} - 1) t | \frac{2 π}{λ}$
There is a Young's double-slit experiment set-up completely dipped in water. Assume that the refractive index of water is $μ_{1}$ . One of the slits is covered with a thin film of thickness t and refractive index $μ_{2}$ . What will be the optical path difference at the centre of screen ?
A $| (μ_{2} - μ_{1}) t |$
B $| (μ_{2} - 1) t |$
C $∣ ∣ ∣ (\frac{μ_{2}}{μ_{1}} - 1) t ∣ ∣ ∣$
D $∣ ∣ ∣ (\frac{μ_{1}}{μ_{2}} - 1) t ∣ ∣ ∣$