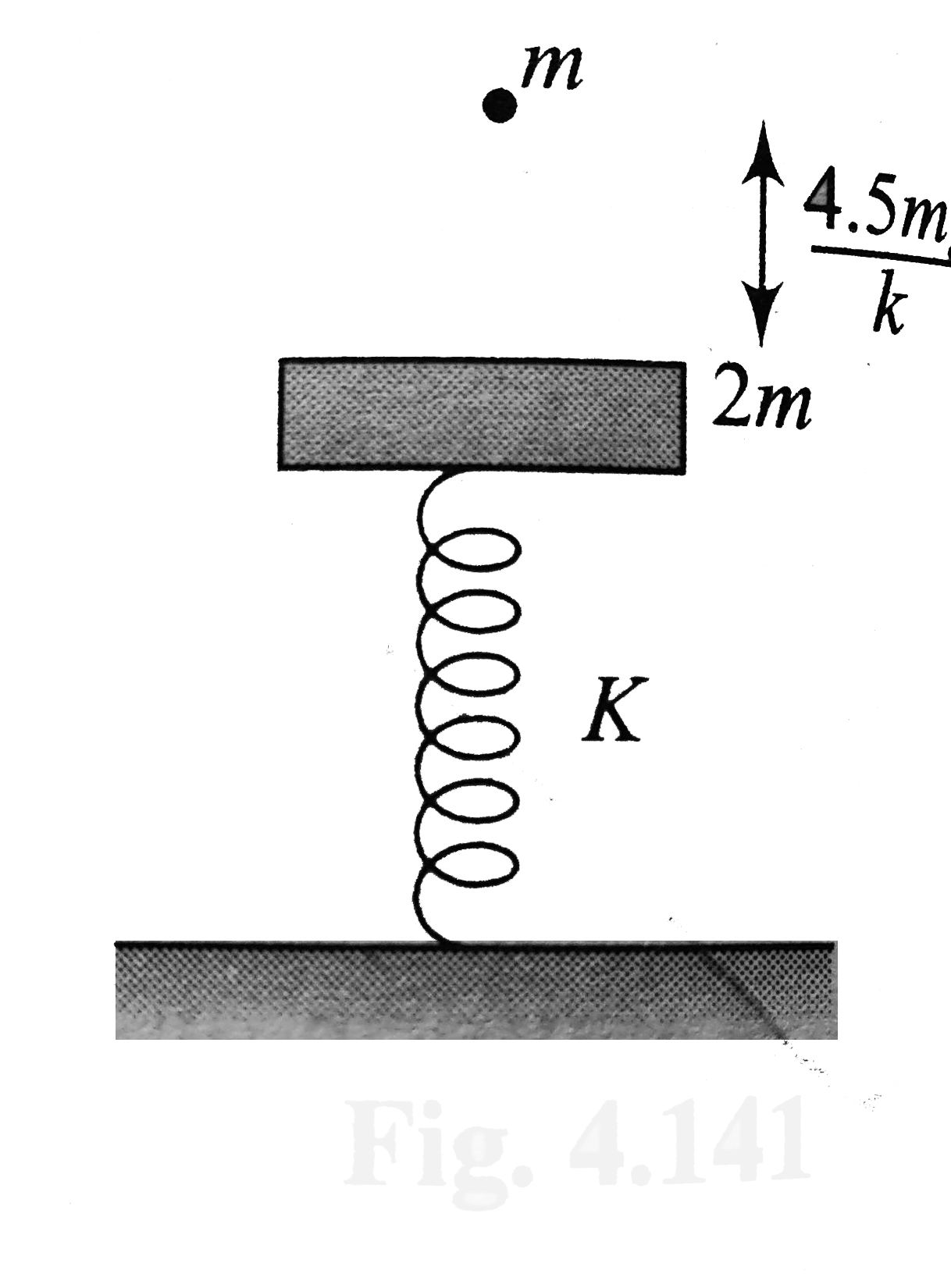
In the figure shown, mass 2m connected with a spring of force constant k is at rest and in equilibrium. A particle of mass m is released from height 4.5mg/k from 2m . The particle stick to the block. Neglecting the duration of collision find time from the release of m to the moment when the spring has maximum compression.
The correct Answer is:5
Velocity of the particle just before collision,
u=√2g×4.5mgK. Now just after collision, velocity (V) of the system of 'plate + particle ' is given by μ=3mV
y=Asin(ωt+ϕ), where A=2mgK,
ϕ=5π6,ω=√K3m
The plate will be at rest again when y=−A
After simplification, t=2π3√3mK=π/5s.
Topper's Solved these Questions
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - LEVEL-I (H.W)
1 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - DISPLACEMENT
6 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - Passage-XIII
1 Videos
- NEWTONS LAWS OF MOTIONBOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION
6 Videos
- PHYSICAL WORLDBOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q
10 Videos
Similar Questions
In the figure shown, mass 2m connected with a spring of force constant k is at rest and in equilibrium. A partical of mass m is released from height 4.5mg/k from 2m . The partical stick to the block. Neglecting the duration of collision find time from the release of m to the moment when the spring has maximum compression.

View SolutionIn the figure shown mass 2m is at rest and in equilibrium. A particle of mass m is released from height 4.5mgk from palte. The particle sticks to the plate. Neglecting the duration of collision. Starting form the when the particles sticks to plate to the time when the spring is in maximum compression for the first time is 2π√mak then find a.
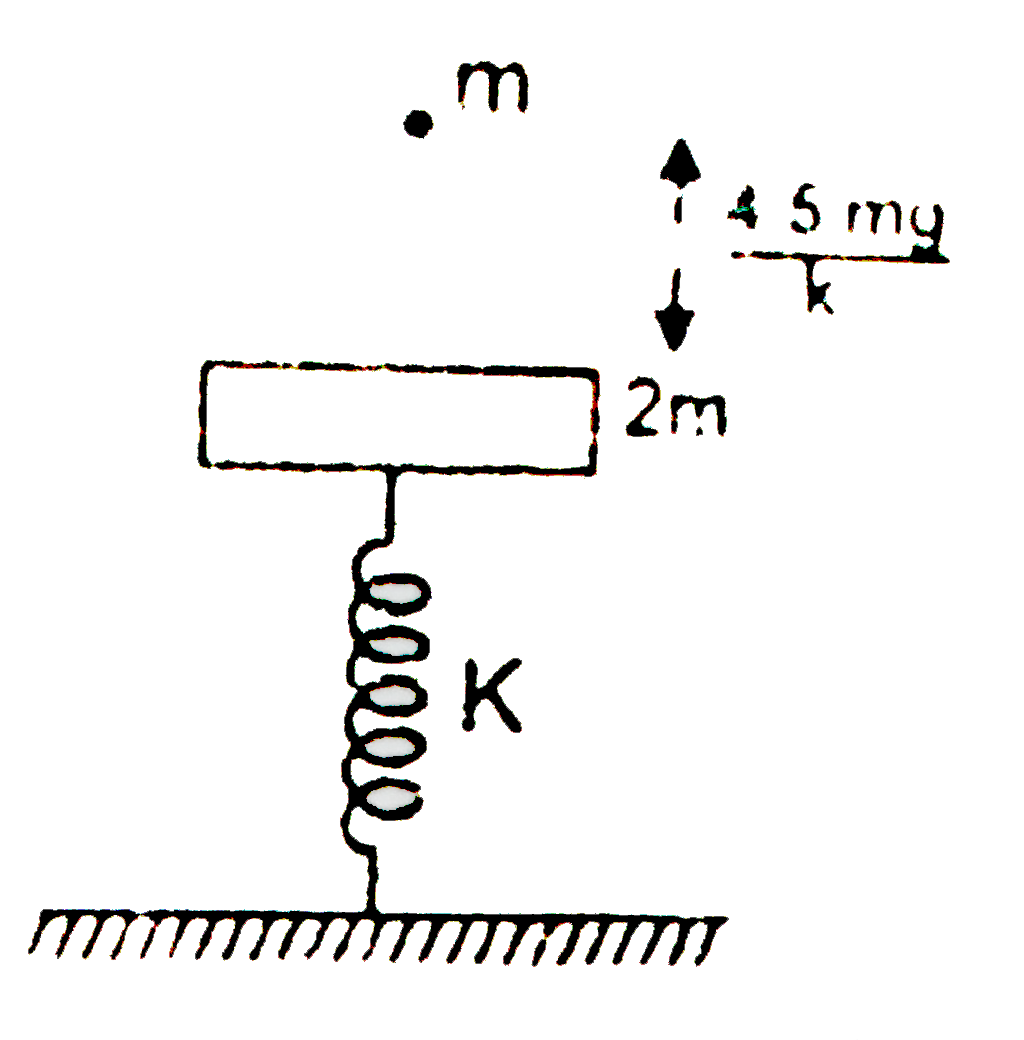
View Solution
Knowledge Check
A particle of mass m is released from rest and follows a particle as a function of time?
 A
A B
B C
C D
D
A block of mass m length force a verical of spring constant k If the block is polled down by a distance of 2mg/k from its equilibrium position and released for the subsequent in the spring to maximum compressed in it mg/k
A2B3C4D1A 2 kg block is connected with two springs of force constants k1=100N/m and k2=300N/m as shown in figure. The block is released from rest with the springs unstretched. The acceleration of the block in its lowest postion is (g=10m/s2)
 AzeroB10m/s2 , upwardsC10m/s2 downwardsD5m/s2 upwards
AzeroB10m/s2 , upwardsC10m/s2 downwardsD5m/s2 upwards
The block shown in figure is released from rest. Find out the speed of the block when the spring is compressed by 1 m

View SolutionA block of mass m is released from a height h from the top of a smooth surface. There is an ideal spring of spring constant k at the bottom of the track. Find the maximum compression in the spring (Wedge is fixed)

View SolutionA block of mass 200 g is suspended by a vertical spring. The spring is stretched by 1.0 cm when the block is in equilibrium. A particle of mass 120 g is dropped on the block from a height of 45 cm. The particle sticks to the block after the impact. Find the maximum extension of the spring. Take g=10m/s2.

View SolutionA block of mass m suspended from a spring of spring constant k. Find the amplitude of S.H.M.
View SolutionA slab S of mass m released from a height h0, from the top of a spring of force constant k. The maximum compression x of the spring is given by the equation.
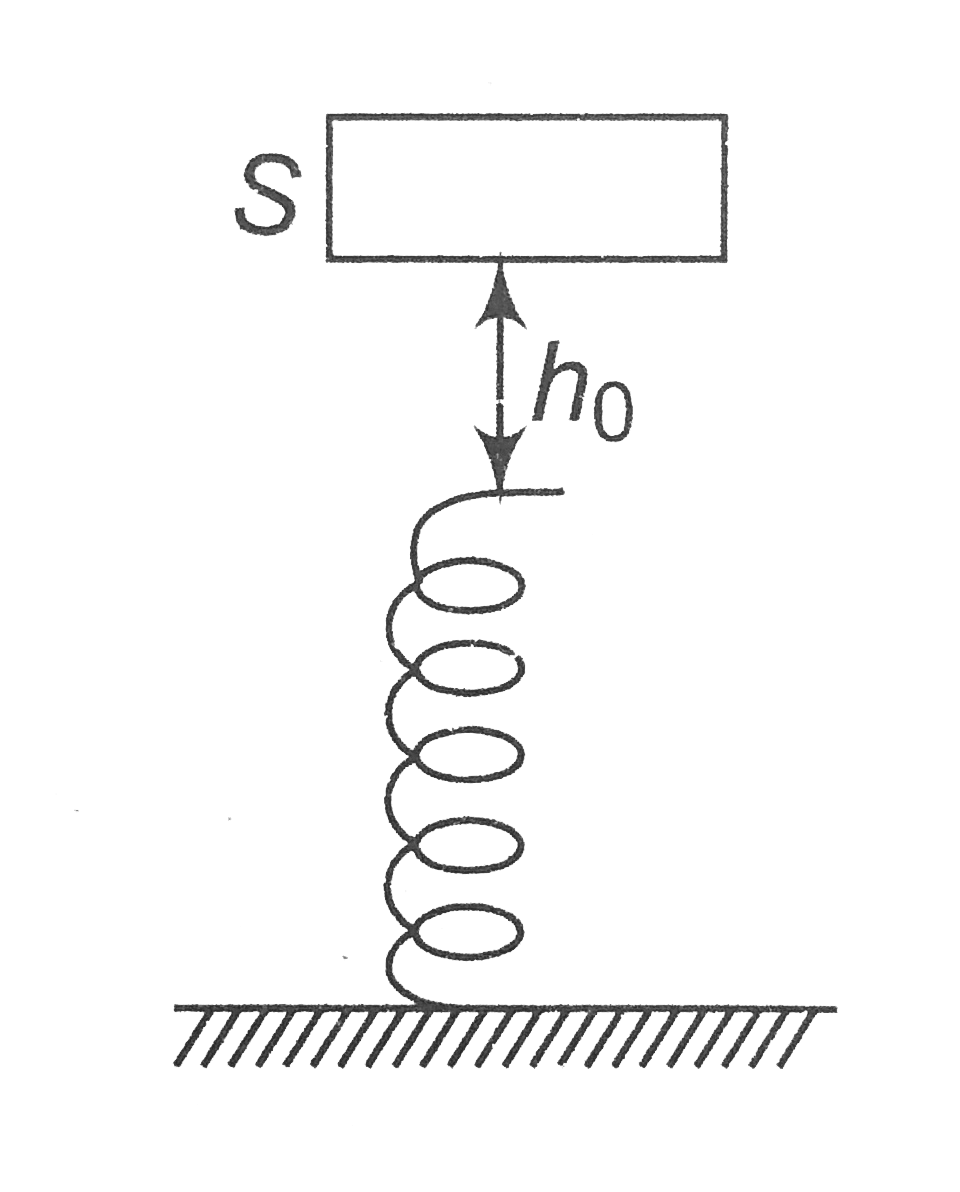
View Solution
