A small ball of mass 1kg is released from a smooth horizontal pipe containing a spring fixed at a height of 20m and 10m away from a vertical wall as shown in the figure. The initial compression of a spring is 2cm and it strikes a smooth vertical wall and smooth horizontal floor repeatedly and elastically as shown. The time period of one complete oscillation (g=10m/s2). (The ball do not collide with walls of the pipe ) is P+π50Q, the value of Q−P is__________
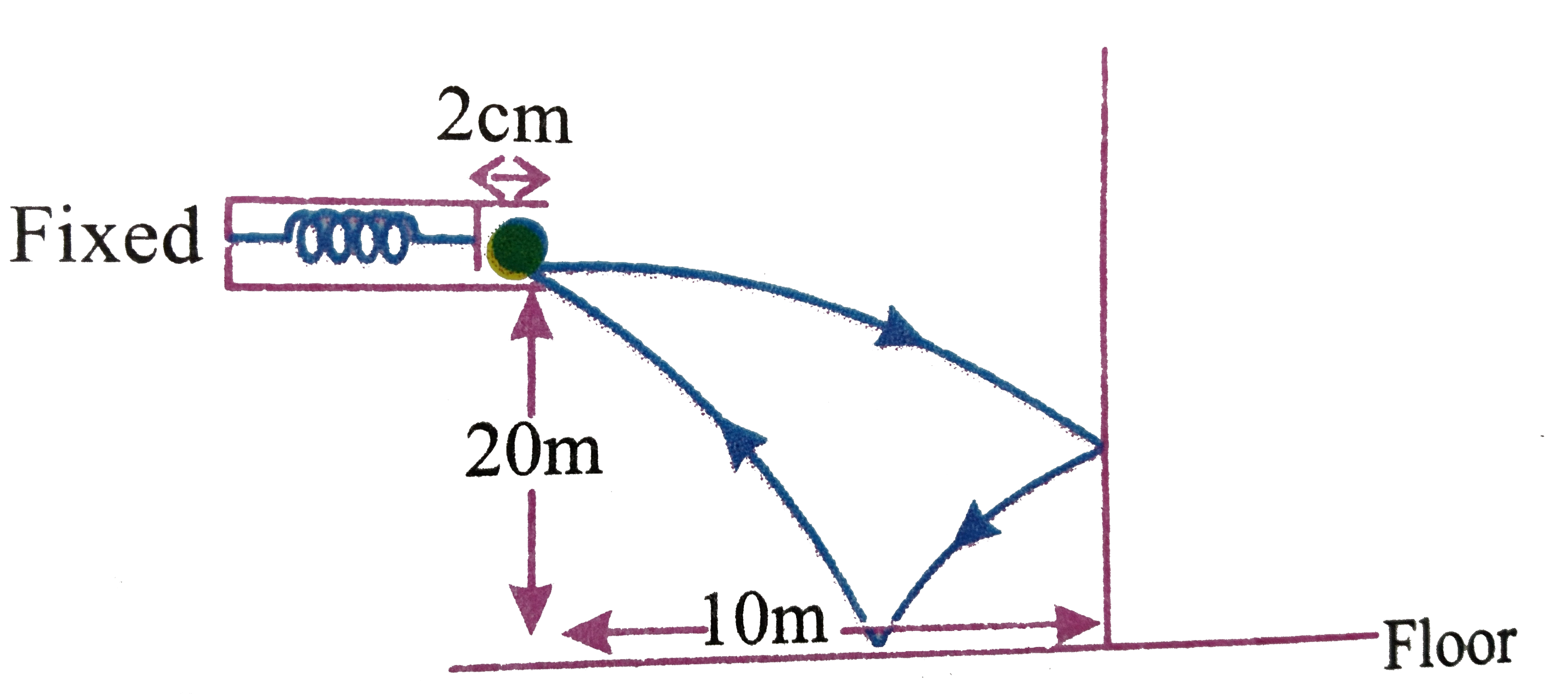
The correct Answer is:1
H=12>2⇒t=2sec
Vx(4)=20⇒Vx=5
12(1)(5)2=k2(2×10−2)2
k=62500
T=4+π√mk
Topper's Solved these Questions
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:LEVEL-I (H.W)
Explore 1 Video
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:DISPLACEMENT
Explore 6 Videos
- OSCILLATIONSBook:NARAYNAChapter:OSCILLATIONSExercise:Passage-XIII
Explore 1 Video
- NEWTONS LAWS OF MOTIONBook:NARAYNAChapter:NEWTONS LAWS OF MOTIONExercise:PASSAGE TYPE QUESTION
Explore 6 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
Similar Questions
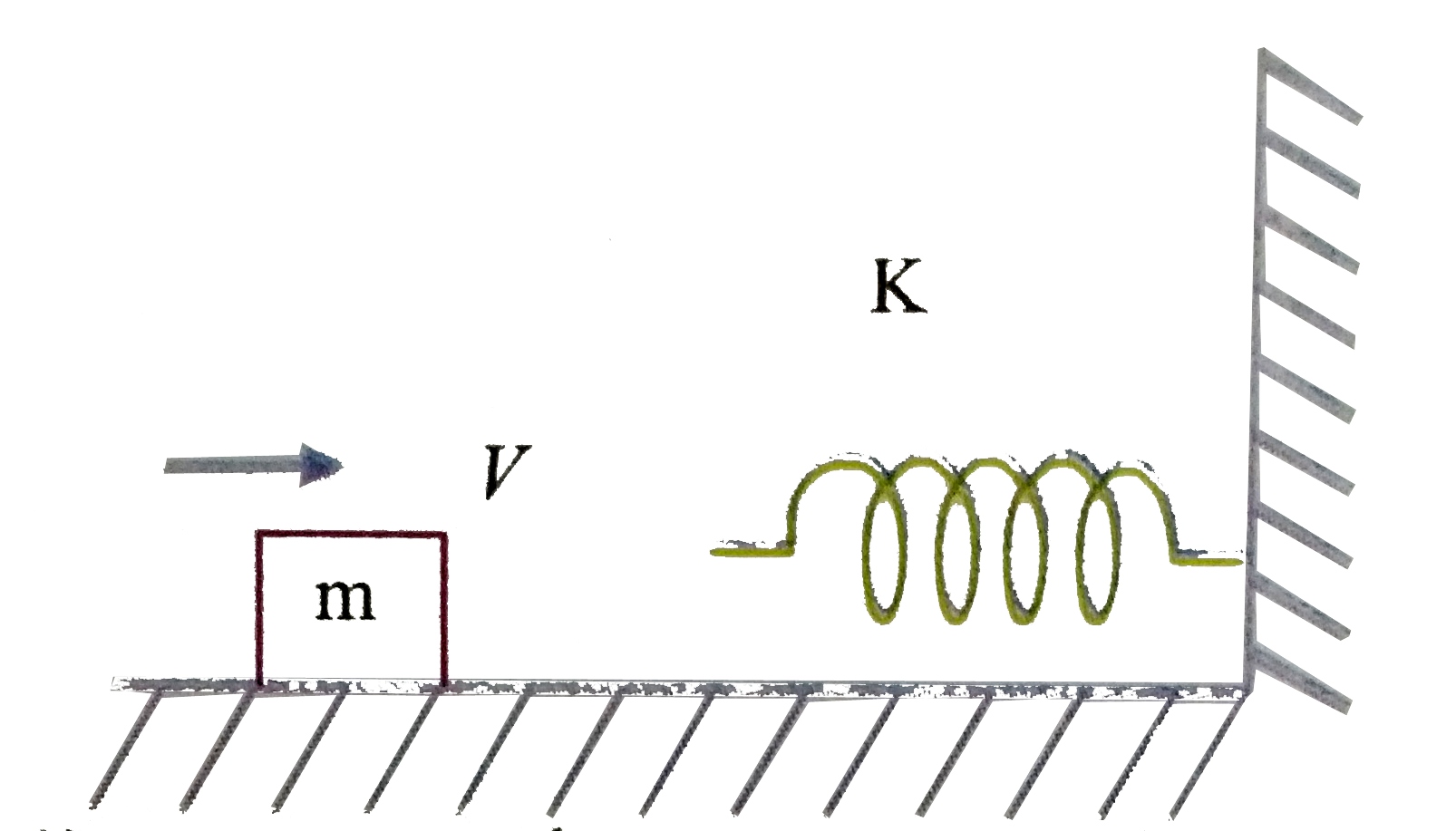
A block of mass m sliding n a smooth horizontal surface with velocity →v meets a long horizontal spring fixed ast one end and having spring constant k as shown n figure. Find the maximum compression of the spring. Will the velocity of the block be the same as v whenit comes back to the original position shown?

View SolutionBlock of mass m is pushed towards a horizontal spring as shown in figure , with initial speed u .

Spring constant of the spring is K and floor is smooth . Calculate maximum possible compression of the spring .
View Solution
Knowledge Check
A ball of mass m=1kg strikes a smooth horizontal floor as shown in figure. The impulse exerted on the floor is
 A(a) 6.25NsB(b) 1.76NsC(c) 7.8NsD(d) 2.2Ns
A(a) 6.25NsB(b) 1.76NsC(c) 7.8NsD(d) 2.2NsA block of 10 g slides on smooth horizontal surface with 20 m/s towards a spring of spring constant 100 N/m placed horizontally (as shown in figure). The maximum compression in spring is
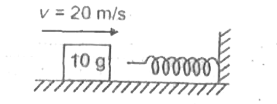 A2 mB0.2 mC20 mD43m
A2 mB0.2 mC20 mD43mA block of mass m=25kg on a smooth horizontal surface with a velocity →v=3ms−1 meets the spring of spring constant k=100N/m fixed at one end as shown in figure. The maximum compression of the spring and velocity of block as it returns to the original position respectively are.
 .A1.5m,−3ms−1B1.5m,0ms−1C1.0m,3ms−1D0.5m,2ms−1
.A1.5m,−3ms−1B1.5m,0ms−1C1.0m,3ms−1D0.5m,2ms−1
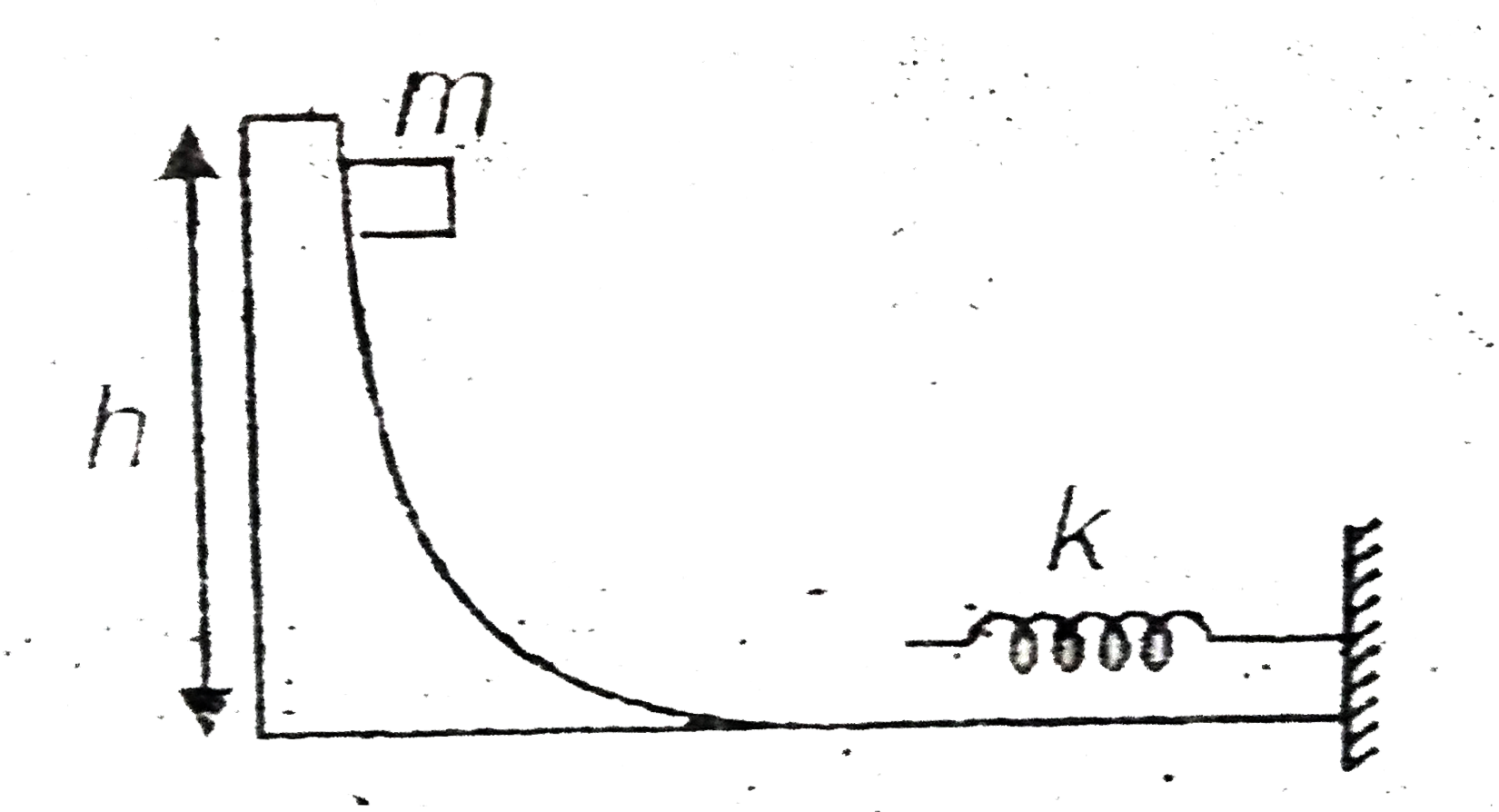
A block of mass m is released from a height h from the top of a smooth surface. There is an ideal spring of spring constant k at the bottom of the track. Find the maximum compression in the spring (Wedge is fixed)
View SolutionTwo blocks of masses m and M connected by a light spring of stiffness k, are kept on a smooth horizontal surface as shown in figure. What should be the initial compression of the spring so that the system will be about to break off the surface, after releasing the block m1?
View SolutionA bullet of mass 'm' is fired from a gum of mass M with a (muzzle) velocity u. If the cart on which gun is fixed can move on the smooth horizontal floor as shown

Find maximum compression of spring of spring constant (K) is
View SolutionThe system shown in the figure can move on a smooth surface. The spring is initially compressed by 6 cm and then released.

View SolutionA particle of mass m is attached to three identical massless springs of spring constant k as shown in the m 135 figure. The time period of vertical oscillation of the particle is

View Solution

