
Two simple pendulums A and B having lengths l and l4 respectively are released from the position as shown in Fig. Calculate the time (in seconds) after which the two strings become parallel for the first time. (Take l=90π2m and g=10ms2.
The correct Answer is:1
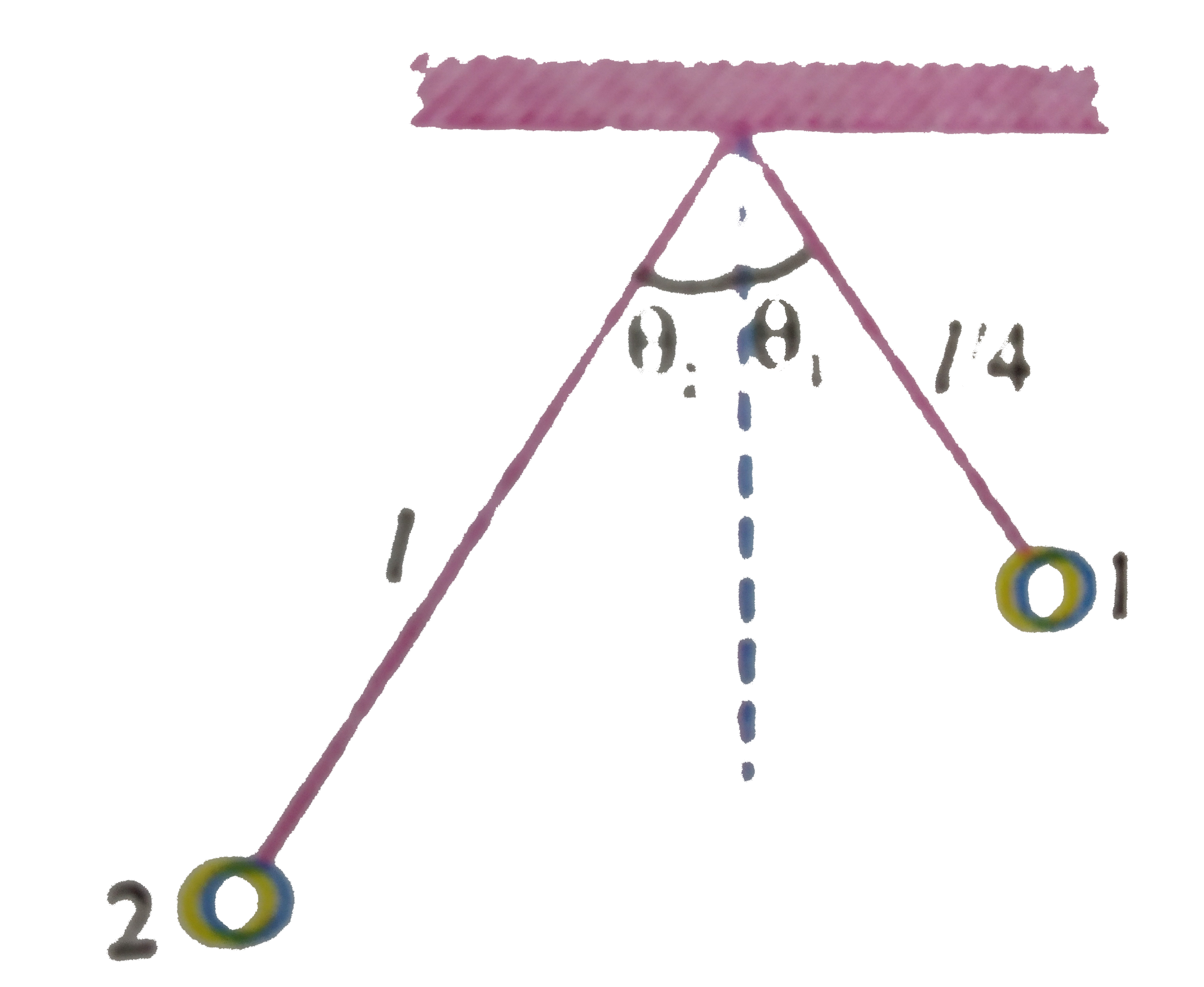 Let T=2π√lg,θ1=θ2
Let T=2π√lg,θ1=θ2
θcos(4πTt)=−θcos(2πTt),4πTt=2nπ±(2πTt+π)
for n=0,t=T/2 for n=1,tT/6,3T/2
the first time meeting, t=T6=π3√lg=1s
Topper's Solved these Questions
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - LEVEL-I (H.W)
1 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - DISPLACEMENT
6 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - Passage-XIII
1 Videos
- NEWTONS LAWS OF MOTIONBOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION
6 Videos
- PHYSICAL WORLDBOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q
10 Videos
Similar Questions
Two simple pendulum A and B having lengths l and l/4 respectively are released from the positions as shown in figure. Calculate the time after which the release of the two strings become parallel for the first time. Angle θ is very small.

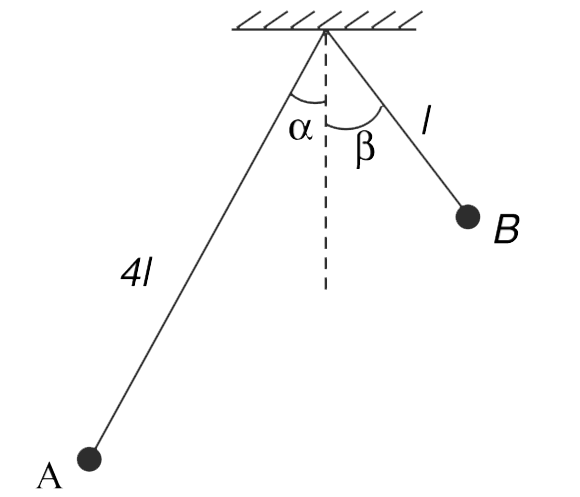
View SolutionTwo simple pendulums A and B have length 4l and l respectively. They are released from rest from the position shown. Both the angles α and β are small. Calculate the time after which the two string become parallel for the first time if-
(a) α=β " " (b)β=1.5α
View Solution
Knowledge Check
Two simple pendulum of length l and 16l are released from the same phase together. They will be at the same time phase after a minimum time.
A8π3√lgBπ3√lgC2sDNone of theseTwo balls of mass m and 2m are attached with strings of length 2L and L respectively. They are released from horizontal position. Find ratio of tensions in the string when the acceleration of both is only in vertical direction :
A3:5B4:5C2:5D1:2Mass of the bob of a simple pendulum of length L is m. If the bob is projected horizontally from its mean position with velocity √4gL, then the tension in the string becomes zero after a vertical displacement of
AL/3B3L/4C4L/3D5L/3
Two simple pendulums of length 1m and 1.21 m are started oscillating from some position. Find the minimum time (in second) after which they again start from same position.
View SolutionTwo simple pendulum have lengths land 25l16 . At t=0 they are in same phase after how may oscillations of smaller pendulum will they be again in phase for first time ?
View SolutionTwo balls are released from the same height at an interval of 2s. When will the separation between the balls be 20m after the first ball is released? Take g=10m/s2.
View SolutionA pendulum has length L = 1.8 m. The bob is released from position shown in the figure. Find the tension in the string when the bob reaches the lowest position. Mass of the bob is 1 kg.

View SolutionA uniform thin rod of length l and mass m is hinged at a distance l/4 from one of the end and released from horizontal position as shown in Fig. The angular velocity of the rod as it passes the vertical position is

View Solution
