Mass of the bob of a simple pendulum of length L is m. If the bob is projected horizontally from its mean position with velocity √4gL, then the tension in the string becomes zero after a vertical displacement of
L/3
3L/4
4L/3
5L/3
The correct Answer is:D
To solve the problem step by step, we will analyze the motion of the bob of the pendulum and determine when the tension in the string becomes zero.
Step 1: Understand the Initial Conditions
The bob of the pendulum has a mass m and is projected horizontally from the mean position with a velocity v=√4gL, where g is the acceleration due to gravity and L is the length of the pendulum.
Hint: Identify the initial velocity and the forces acting on the bob when it is projected.
Step 2: Identify Forces Acting on the Bob
When the bob moves upward, two forces act on it:
1. The gravitational force mg acting downward.
2. The tension T in the string acting upward.
As the bob moves, it also experiences centripetal acceleration due to its circular motion.
Hint: Recall that the centripetal force required to keep the bob moving in a circular path is provided by the tension in the string minus the component of gravitational force acting along the direction of the string.
Step 3: Condition for Zero Tension
The tension in the string becomes zero when the centripetal force required for circular motion is exactly equal to the component of the gravitational force acting along the string. This can be expressed as:
T=mv2L−mgcos(θ)=0
Where θ is the angle the string makes with the vertical.
Hint: Set up the equation for tension and solve for the conditions when T=0.
Step 4: Kinetic and Potential Energy Considerations
At the highest point where tension is zero, the bob has converted some of its kinetic energy into potential energy. The initial kinetic energy when the bob is at the mean position is:
KEi=12mv2=12m(4gL)=2mgL
At a height h above the mean position, the potential energy is:
PE=mgh=mgL(1−cos(θ))
Hint: Use conservation of energy to relate the initial kinetic energy to the potential energy at the height h.
Step 5: Set Up the Energy Equation
Using conservation of energy:
KEi=PE
2mgL=mgL(1−cos(θ))+12mv2
Since the tension is zero, we can assume v2=gLsin(θ) at that point.
Hint: Substitute v2 into the energy equation to find the relationship between h and θ.
Step 6: Solve for θ
From the energy conservation equation, we can simplify and solve for θ:
2=1−cos(θ)+12sin(θ)
Rearranging gives:
1+12sin(θ)=0
This leads to:
sin(θ)=23
Hint: Use the relationship h=L(1−cos(θ)) to find the vertical displacement h.
Step 7: Calculate the Height h
Using the identity sin2(θ)+cos2(θ)=1:
cos(θ)=√1−(23)2=√59=√53
Now, the height h can be calculated:
h=L(1−cos(θ))=L(1−√53)=L(3−√53)
After calculating, we find:
h=5L3
Final Answer
The vertical displacement after which the tension in the string becomes zero is:
5L3
---
The bob of the pendulum has a mass m and is projected horizontally from the mean position with a velocity v=√4gL, where g is the acceleration due to gravity and L is the length of the pendulum.
When the bob moves upward, two forces act on it:
1. The gravitational force mg acting downward.
2. The tension T in the string acting upward.
The tension in the string becomes zero when the centripetal force required for circular motion is exactly equal to the component of the gravitational force acting along the string. This can be expressed as:
T=mv2L−mgcos(θ)=0
Where θ is the angle the string makes with the vertical.
At the highest point where tension is zero, the bob has converted some of its kinetic energy into potential energy. The initial kinetic energy when the bob is at the mean position is:
KEi=12mv2=12m(4gL)=2mgL
PE=mgh=mgL(1−cos(θ))
Using conservation of energy:
KEi=PE
2mgL=mgL(1−cos(θ))+12mv2
From the energy conservation equation, we can simplify and solve for θ:
2=1−cos(θ)+12sin(θ)
1+12sin(θ)=0
This leads to:
sin(θ)=23
Using the identity sin2(θ)+cos2(θ)=1:
cos(θ)=√1−(23)2=√59=√53
h=L(1−cos(θ))=L(1−√53)=L(3−√53)
h=5L3
The vertical displacement after which the tension in the string becomes zero is:
5L3
Topper's Solved these Questions
- WORK POWER AND ENERGYBOOK - NARAYNACHAPTER - WORK POWER AND ENERGYEXERCISE - NCERT (Based Questions)
45 Videos
- WORK POWER AND ENERGYBOOK - NARAYNACHAPTER - WORK POWER AND ENERGYEXERCISE - Level-V (Single Answer)
24 Videos
- WORK POWER AND ENERGYBOOK - NARAYNACHAPTER - WORK POWER AND ENERGYEXERCISE - Level- II (C.W)
68 Videos
- WORK , ENERGY & POWER BOOK - NARAYNACHAPTER - WORK , ENERGY & POWER EXERCISE - EXERCISE IV
43 Videos
Similar Questions
The bob of a simple pendulum of length 1m hangs at rest. It is suddenly projected horizontally with velocity 10ms−1. Calculate the velocity of the bob and tension of the string when it is horizontal. The mass of the bob is 12kg.
[Hint : See worked out example 4]
View SolutionBob of a simple pendulum of length L is projected horizontally with a speed of u=√4gh, , from the lowest position. Find the distance of the bob from vertical line AB, at the moment its tangential acceleration becomes zero.
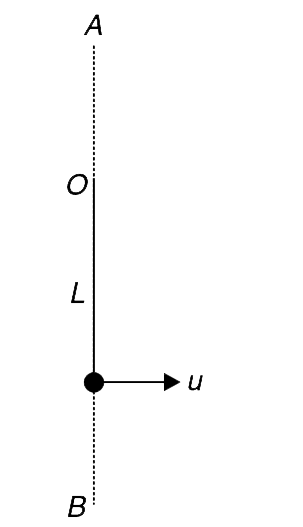
View Solution
Knowledge Check
The bob of a simple pendulum of length L, is displaced through 90∘, from its mean position and then released. What will be the tension in the string when the bob of mass m will be its lowest position ?
AmgB2 mgC3 mgD6 mgThe bob of a simple pendulum of length L, is displaced through 90∘, from its mean position and then released. What will be the tension in the string when the bob of mass m will be at its lowest position?
AmgB3 mgC2 mgD6 mgA particle suspended by a light inextensible thread of length l is projected horizontally from its lowest position with velocity √7gl/2. The string will slack after swinging through an angle equal to
A30∘B90∘C120∘D150∘
The bob of a simple pendulum of length l is given a sharp hit to impart it a horizontal speed of √3gl . When it was at its lowermost position. Find
angle α shown of the string from upside of vertical and speed of the particle when the string becomes slack.

View SolutionA pendulum has length L = 1.8 m. The bob is released from position shown in the figure. Find the tension in the string when the bob reaches the lowest position. Mass of the bob is 1 kg.

View SolutionA simple pendulum has a bob of mass m and string of length R. The bob is projected from lowest position giving it a horizontal velocity just enough for it to complete the vertical circle. Let the angular displacement of the pendulum from its initial vertical position be represented by θ. Plot the variation of kinetic energy (kE) of the bob and the tension (T) in the string with θ. Plot the graph for one complete rotation of the pendulum.
View SolutionIf the inertial mass m1 of the bob of a simple pendulum of length 'l' is not equal to the gravitationalmassmg, then its period is
View SolutionThe velocity of the bob of a simple pendulum in the mean position is v. If its amplitude is doubled, by keeping the same length, then its velocity in the mean position will be
View Solution
