A simple pendulum is oscillating with an angular amplitude of $90^{\circ}$ as shown in the figure. The value of $θ$ for which the resulting acceleration of the bob is directed (i) vertically downward, (ii) vertically upward and (iii) horizontally is

A

$0^{0}, {cos}^{- 1} (\frac{1}{\sqrt{3}}), 90^{0}$

B

$90^{0}, {cos}^{- 1} (\frac{1}{\sqrt{3}}), 0^{0}$

C

${cos}^{- 1} (\frac{1}{\sqrt{3}}), 0^{0}, 90^{0}$

D

${cos}^{- 1} (\frac{1}{\sqrt{3}}), 90^{0}, 0^{0}$ .

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

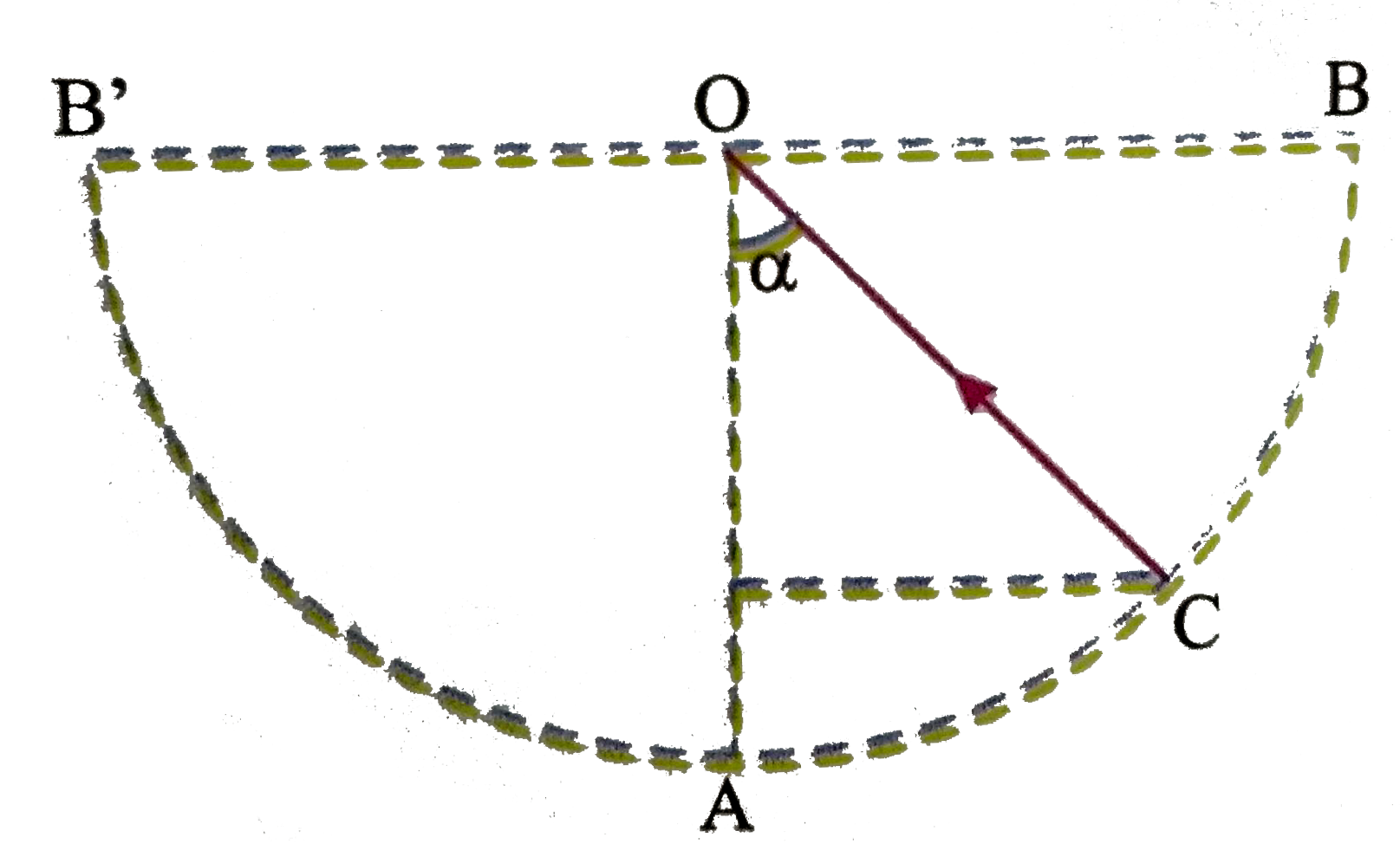
At "C", $T cos α = M g$ …(i)
$P . E_{B} = K . E_{A} \Rightarrow m g r = \frac{1}{2} m v_{A}^{2}$
hence at $C, v = \sqrt{v_{A}^{2} - 2 g r (1 - cos α)}$
$T - m g cos α = \frac{M v^{2}}{r} = \frac{M .2 g r cos α}{r}$ .

|

Updated on:21/07/2023

Class 11 PHYSICS WORK, ENERGY AND POWER

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A simple pendulum is vibrating with an angular amplitude of $90^{\circ}$ as shown in the figure. For what value of a is the acceleration directed

i) vertically upwards
ii) horizontally
iii) vertically downward
A $0^{\circ}, {cos}^{- 1} (\frac{1}{\sqrt{3}}), 90^{\circ}$
B $90^{\circ}, {cos}^{- 1} (\frac{1}{\sqrt{3}}), 0^{\circ}$
C ${cos}^{- 1} (\frac{1}{\sqrt{3}}), 0^{\circ}, 90^{\circ}$
D ${cos}^{- 1} (\frac{1}{\sqrt{3}}), 90^{\circ}, 0^{\circ}$
Question 2 - Select One
A simple pendulum is vibrating with an angular amplitude of $90^{\circ}$ as shown in figure. For what value of $α$ (angle between string and vertical) during its motion, the total acceleration is directed horizontally ?

A ${tan}^{- 1} (\frac{1}{2})$
B ${tan}^{- 1} (\frac{1}{\sqrt{2}})$
C ${cos}^{- 1} (1 / \sqrt{3})$
D ${sin}^{- 2} (1 / \sqrt{3})$
Question 3 - Select One
A simple pendulum is oscillating with an angular amplitude $60^{\circ}$ . If mass of bob is $50$ gram, then the tension in the string at mean position is $(g = 10 m s^{- 2})$
A0.5 N
B1 N
C1.5 N
D2 N

NARAYNA-WORK POWER AND ENERGY-Level- III (C.W)

Home
Ask Doubt
Profile