A particle strikes a horizontal frictionless floor with a speed 'u' at an angle 'theta' with the vertical and rebounds with a speed 'v' at an angle 'alpha' with the vertical. Find the value of 'v' if 'e' is the coefficient of restitution.
The correct Answer is:B
.
Topper's Solved these Questions
- WORK POWER AND ENERGYBOOK - NARAYNACHAPTER - WORK POWER AND ENERGYEXERCISE - NCERT (Based Questions)
45 Videos
- WORK POWER AND ENERGYBOOK - NARAYNACHAPTER - WORK POWER AND ENERGYEXERCISE - Level-V (Single Answer)
24 Videos
- WORK POWER AND ENERGYBOOK - NARAYNACHAPTER - WORK POWER AND ENERGYEXERCISE - Level- II (C.W)
68 Videos
- WORK , ENERGY & POWER BOOK - NARAYNACHAPTER - WORK , ENERGY & POWER EXERCISE - EXERCISE IV
43 Videos
Similar Questions
A particle of mass m strikes a horizontal smooth floor with velocity u making an angle θ with the floor and rebound with velocity v making an angle θ with the floor. The coefficient of restitution between the particle and the floor is e. Then
View SolutionA projectile is fired with a speed u at an angle θ with the horizontal. Find its speed when its direcrtion of motion makes an angle α with the horizontal.
View Solution
Knowledge Check
A particle strikes a horizontal frictionless floor with a speed u, at an angle θ with the vertical, and rebounds with a speed υ, at an angle ϕ with the vertical. The coefficient of restitution between the particle and the floor is e. The angle ϕ is equal to :
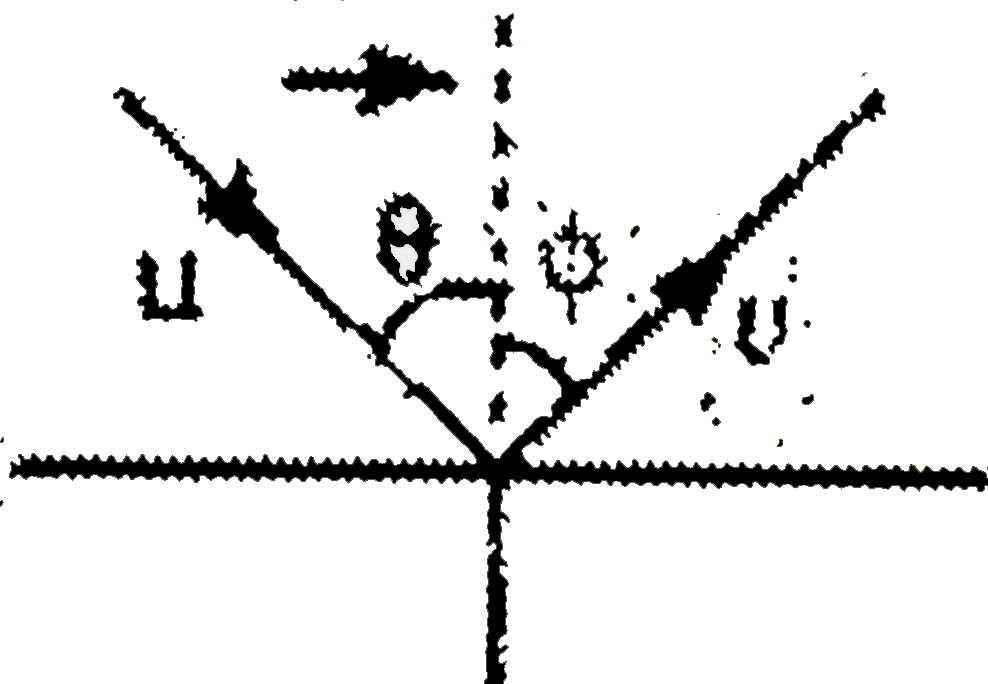 AθBtan−1[etanθ]Ctan−![1etanθ]D(1+e)θ
AθBtan−1[etanθ]Ctan−![1etanθ]D(1+e)θA particle strikes a horizontal frictionless floor with a speed u at an angle θ with the vertical, and rebounds with a speed v at an angle ϕ with vertical. The coefficient of restitution between the particle and floor is e. The magnitude of v is
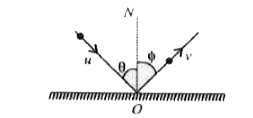 AeuB(1−e)uCu√e2sin2θ+cos2θDu√sin2θ+e2cos2θ
AeuB(1−e)uCu√e2sin2θ+cos2θDu√sin2θ+e2cos2θA particle strikes a horizontal frictionless floor with a speed u at an angle θ with the vertical, and rebounds with a speed v at an angle ϕ with vertical. The coefficient of restitution between the particle and floor is e. The angle ϕ is equal to
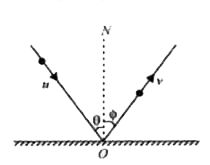 AθB(1+e)θCtan−1(etanθ)Dtan−1(1etanθ)
AθB(1+e)θCtan−1(etanθ)Dtan−1(1etanθ)
A particle is thrown with speed u of an angle theta with the horizontal when the particle makes an angle phi with the horizontal its speed changes to v
View SolutionA particle strikes a horizontal frictionless floor with a speed u, at an angle θ to the vertical, and rebounds with a speed v, at an angle ϕ to the vertical. The coefficient of restitution between the particle and the floor is e. The magnitude of v is
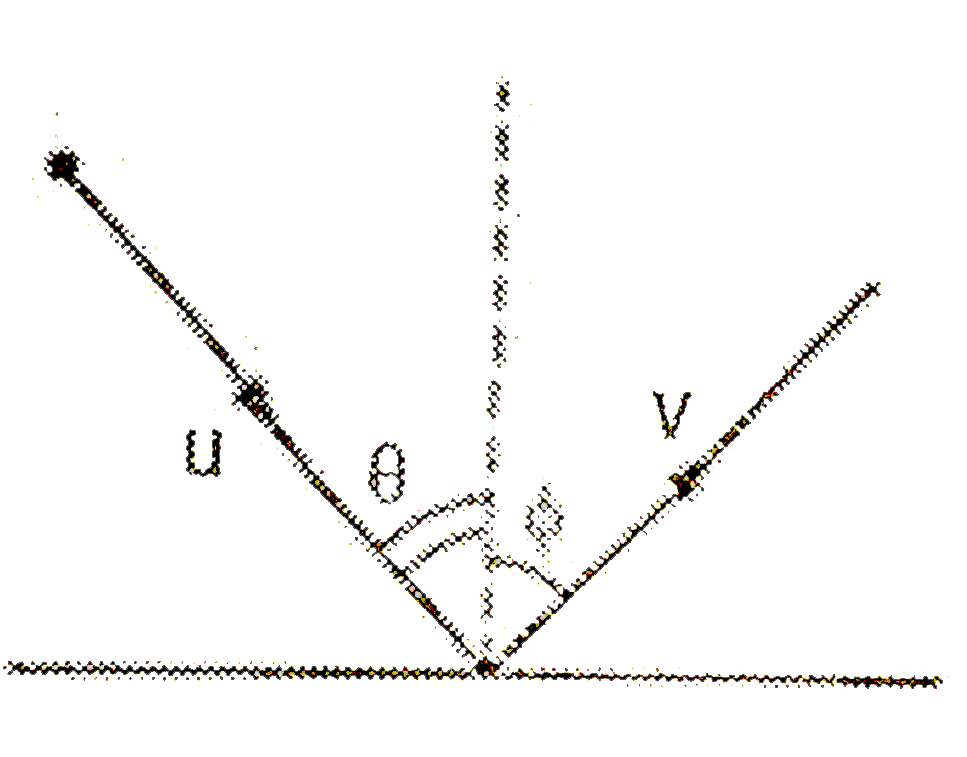
View SolutionA particle strikes a horizontal smooth floor with a velocity u making an angle θ with the floor and rebounds with velocity v making an angle ϕ with the floor. The coefficient of restitution between the particle and the floor is e.
View SolutionA particle strikes a horizontal smooth floor with a velocity a making an angle θ with the floor and rebounds with velocity v making an angle ϕ with the floor. If the coefficient of restitution between the particle and the floor is e, then
View SolutionA particle is thrown with a speed u at an angle θ with the horizontal. When the particle makes an angle ϕ with the horizontal. Its speed changes to v :
View Solution
