The system shown is lying on a smooth horizontal surface. Mass m is constrained to move along the line 3. Springs 1 and 2 at right angles with respect to one another are symmetrically arranges with respect to 3 which is an elastic cord. The force constants of 1,2 and 3are k each and they are all just taut in the condition shown. For small oscillations of m along 3, time period is π√myk(1+√x). The valye of xy is___________

The correct Answer is:4
(1) Let m be displaced to left by x.
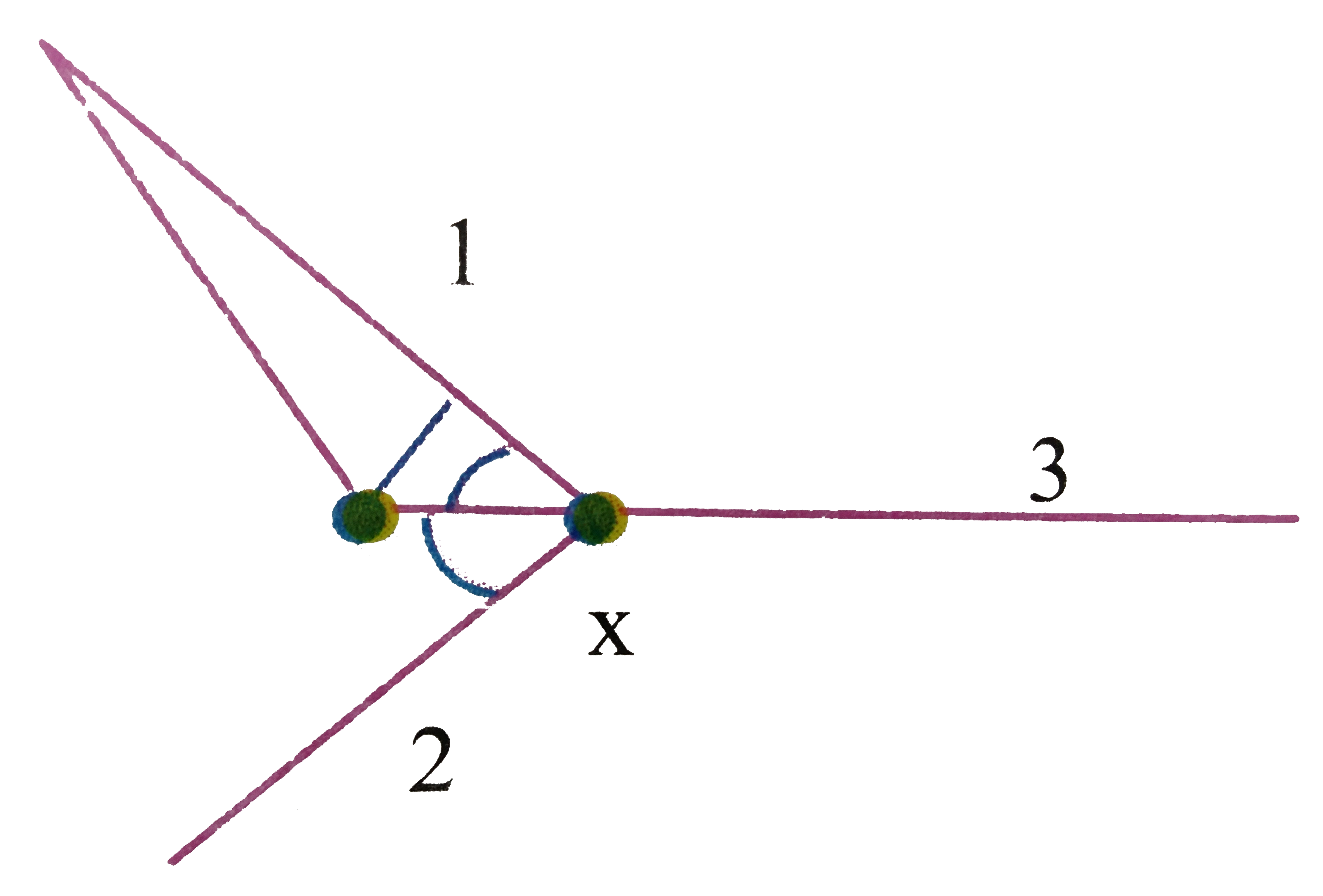
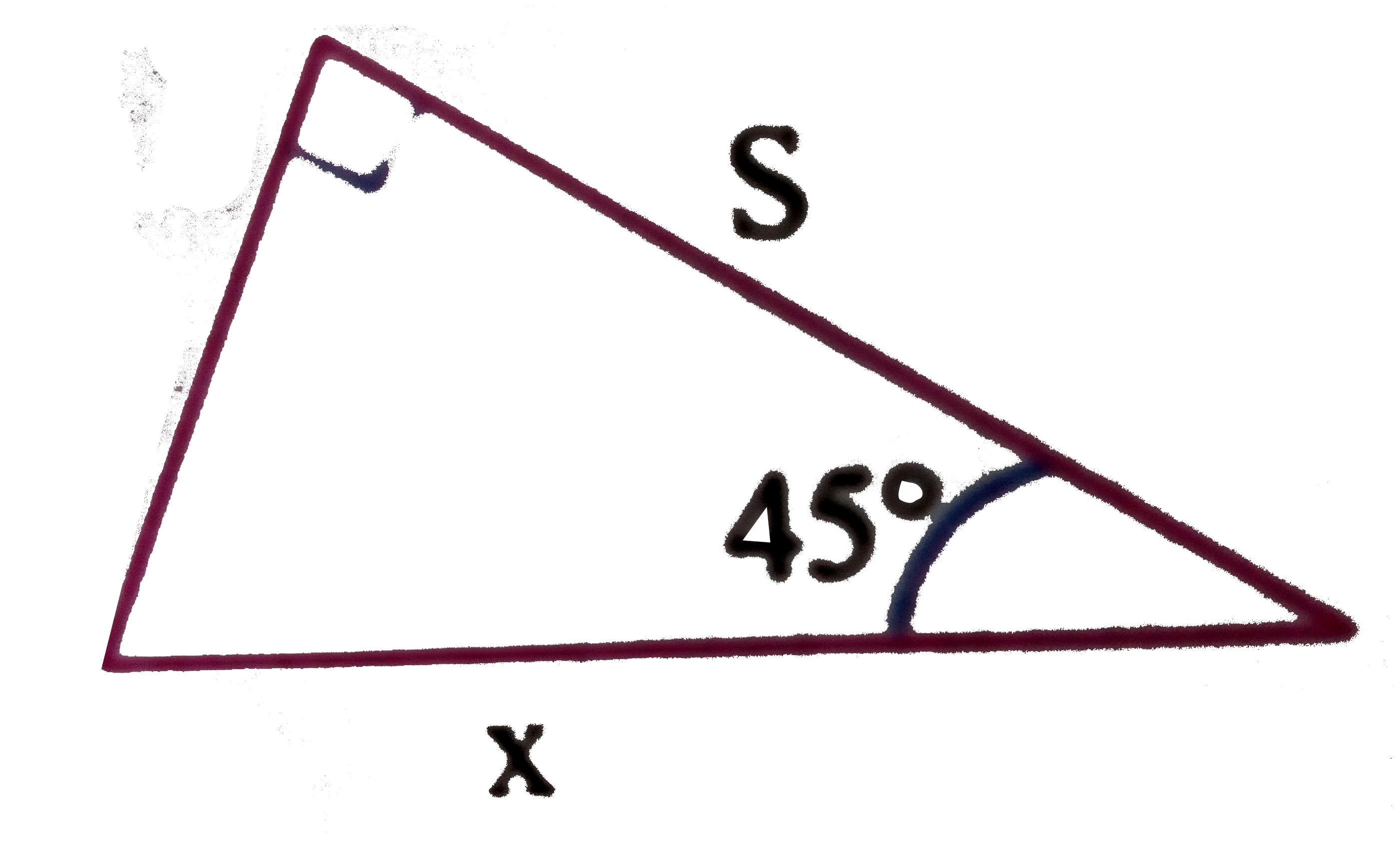
Elongation of spring is S=xcos45
Spring force is 2kScos45∘ along left 2kxcos245∘=ikx
Force due to cord =kx
Restoring force for leftward deflection is 2kx
2kx=ma
For left T1=2π√m2k
(2) For right cord becomes slack and only springs provoded restoring force.
Restoring force =kx
kx=maT2=2π√mk
For complete cycle, time period =12 of T1+12 of T2
=π√m2K+π√mk=π√m2k(1+√2)
Topper's Solved these Questions
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - LEVEL-I (H.W)
1 Video
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - DISPLACEMENT
6 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - Passage-XIII
1 Video
- NEWTONS LAWS OF MOTIONBOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION
6 Videos
- PHYSICAL WORLDBOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q
10 Videos
Similar Questions
Two springs are jonied and connected to a mass m as shown in figure. If the force constants of the two springs are k1andk2, shown that frequency of oscillation of mass m is

View SolutionA block of mass m is connected between two springs (constants K1 and K2) as shown in the figure and is made to oscillate, the frequency of oscillation of the system shall be-

View Solution
Knowledge Check
A block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is
 A√2mkv0B√mk.v0C√mk.v0Dm2k.v0
A√2mkv0B√mk.v0C√mk.v0Dm2k.v0
A mass m is suspended from a spring of force constant k and just touches another identical spring fixed to the floor as shown in the fig. The time period of small oscillations isA2π√mkBπ√mk+π√mk2Cπ√m3k2Dπ√mk+π√m2kA mass m is suspended from a spring of force constant k and just touches another idential spring fixed to the floras shown in the figure. The time period of small oscillation is
 A2π√mkBπ√mk+π√mk/2Cπ√m3k/2Dπ√mk+π√m2k
A2π√mkBπ√mk+π√mk/2Cπ√m3k/2Dπ√mk+π√m2k
Two spring of spring constants k1 and k2 ar joined and are connected to a mass m as shown in the figure. Calculate the frequency of oscillation of mass m.

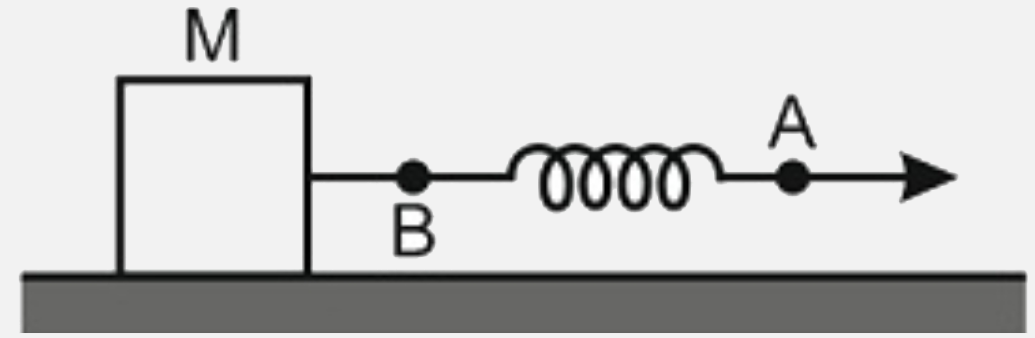
View SolutionA block of mass M is placed on a smooth horizontal surface and it is pulled by a light spring as shown in the diagram. If the ends A and B of the spring are moving with 4 ms−1 and 2 ms−1 respectively and the rate at which spring energy is increasing is 20 Js−1. then what is the value of spring force (in N)?
View SolutionA horizontal force F is applied on a riing of mass m1 constrained to move on a horizontal smooth wire the hanging mass m2 is constant angle with

View SolutionA mass M is suspended by two springs of force constants K1andK2 respectively as shown in the diagram. The total elongation (stretch) of the two springs is

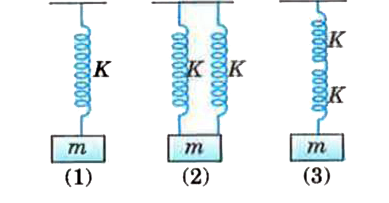
View SolutionThe figure shows the arrangement of block of mass m with one or more identical springs in three different ways . If Force cosntant of each springs is K and T1, T2 and T3 are the time periods of oscillations of the arrangement 1, 2, and 3, respectibely, then
View Solution