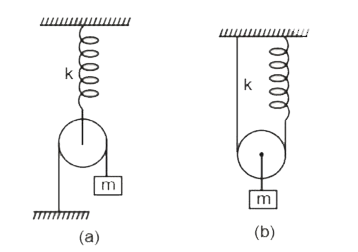
Figure shows a system consisting of a massles pulley, a spring of force constant k and a block of mass m. If the block is sligthtly displaced vertically down from its equilibrium and released, find the period of its vertical oscillation in cases (a) and (b).

Let the block is displacement down a small displacement ment 'y'. The corresponding
extension of spring will be y2. The extra force devolved in the spring is Ky2. If T be the tension in the string, then
2T=Ky2 or T=Ky4
The restoring force on the block
Frest=−T=−Ky4 and a=Frestm=K4m(−y)
As force is proportional to the displacement form mean postion, so it represents SHM. compering with standard equation of SHM,a=−ω2y, we get ω=√K4m and time period T=2πω=2π√4mK
Note: The expression T=2π√4mk can be written as T=2π√mkeff, where keff=k4. The given device is equivalent to a block of mass m connected to a spring of force constant keff.
Topper's Solved these Questions
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - C.U.Q
78 Videos
- OSCILLATIONSBOOK - NARAYNACHAPTER - OSCILLATIONSEXERCISE - LEVEL -I (C.W)
34 Videos
- NEWTONS LAWS OF MOTIONBOOK - NARAYNACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - PASSAGE TYPE QUESTION
6 Videos
- PHYSICAL WORLDBOOK - NARAYNACHAPTER - PHYSICAL WORLDEXERCISE - C.U.Q
10 Videos
Similar Questions
Figure shows a system consisting of a massless pulley, a spring of force constant k and ablock of mass m. If the block is slightly displaced vertically down from its equillibrium position and then released, find the period of its vertical oscillation in cases (a) & (b).
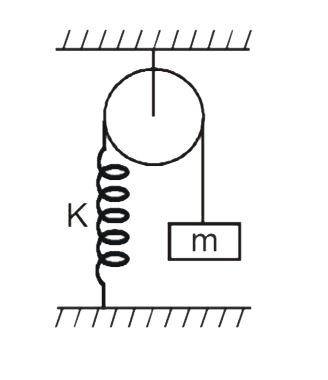
View SolutionFigure shows a system consisting of pulley having radius R, a spring of force constant k and a block of mass m. Find the period of its vertical oscillation.
View Solution
Knowledge Check
Figure shows a system consisting of a massless pulley, a spring of force constant k and a block of mass m. If the block is slightly displaced vertically down from is equilibrium position and then released, the period of its vertical oscillation is
 A2π√mKBπ√m4KCπ√mKD4π√mK
A2π√mKBπ√m4KCπ√mKD4π√mKThree springs of each force constant k are connected as shown figure. Point mass m is slightly displaced to compress A and released. Time period of oscillation is
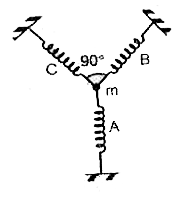 A2π√m2kB2π√m3kC2π√mkD2π√mk+√2(k+1)
A2π√m2kB2π√m3kC2π√mkD2π√mk+√2(k+1)An elastic string of constant k is attached to a block of mass m as shown. The block is given an extension of 2mgk from the equilibrium position and released. The time period of oscillations of the block is
 A2π√mkB4√mk(π3+√3)C2π√mk+2√3√mkDπ√mk+√3√mk
A2π√mkB4√mk(π3+√3)C2π√mk+2√3√mkDπ√mk+√3√mk
In the following arrangements, bock is slightly displaced vertically down from its equilibrium position and released. Find time period of vertical oscillations. The pulley is light.

View SolutionA system shown in the figure consists of a massless pulley, a spring of force constant k displaced vertically downwards from its equilibrium position and released, then the Period of vertical oscillations is

View SolutionA block of mass m hangs from a vertical spring of spring constant k. If it is displaced from its equilibrium position, find the time period of oscillations.
View SolutionFind the period of a vertical spring - block system by both methods.
View SolutionA block of mass m is connected with two ideal pullies and a massless spring of spring constant K as shown in figure. The block is slightly displaced from its equilibrium position. If the time period of oscillation is μπ√mK. Then find the value of μ.

View Solution
