Two walls of thicknes l1 and l2 and ther-mal condctivities K1 and K2 are in contact In the steady state, if the temperature at the outer faces are T1 and T2 find the temperature at the common wall .
Let θ be the temperature of the junction or interface In steady stateQt = constant
∴K1A(θ1−θ)l1=K2A(θ−θ)l2
K1θ1l1+K2θ2l2K1l1+K2l2=K1θ1l2+K2θ2l1K1l2+K2l1
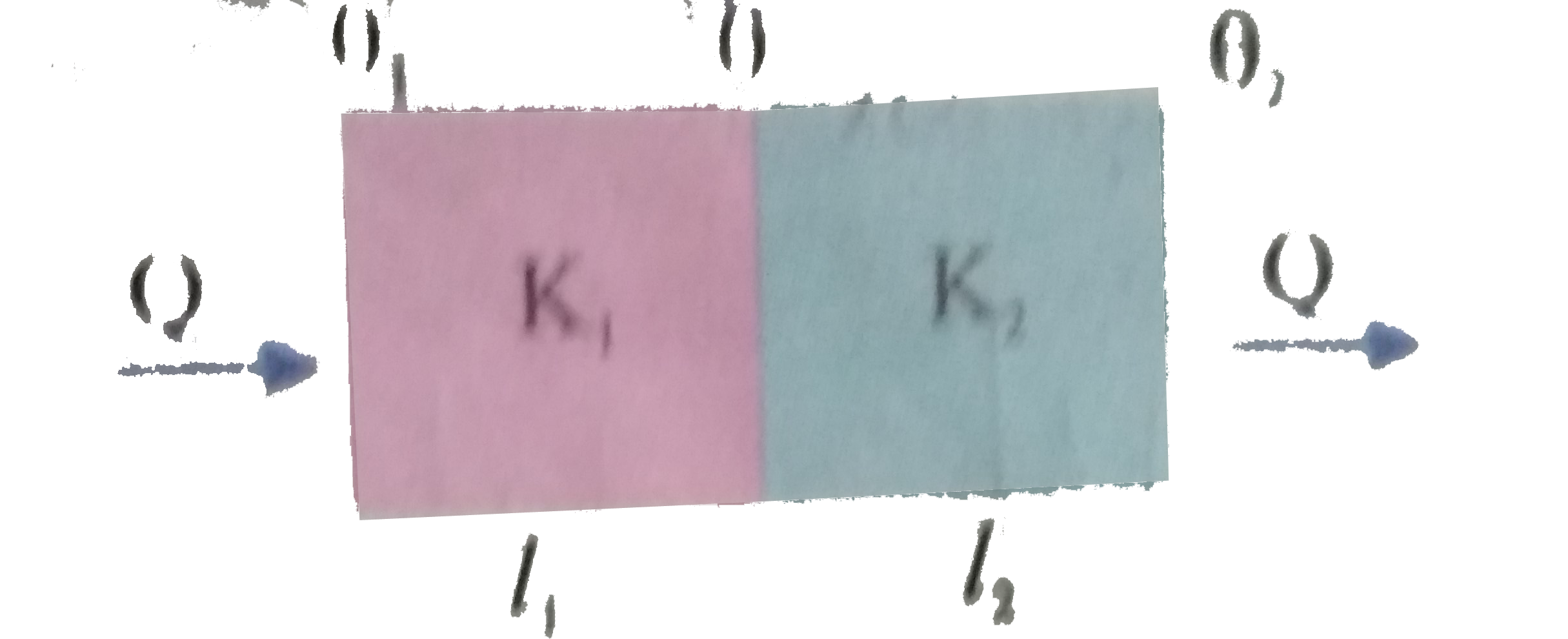 .
.
Topper's Solved these Questions
- TRANSMISSION OF HEATBook:NARAYNAChapter:TRANSMISSION OF HEATExercise:C .U .Q
Explore 89 Videos
- TRANSMISSION OF HEATBook:NARAYNAChapter:TRANSMISSION OF HEATExercise:LEVEL -1 (C.W)
Explore 1 Video
- THERMODYNAMICSBook:NARAYNAChapter:THERMODYNAMICSExercise:Exercise
Explore 187 Videos
- UNITS AND MEASUREMENTSBook:NARAYNAChapter:UNITS AND MEASUREMENTSExercise:STATEMENT TYPE QUESTION
Explore 23 Videos
Similar Questions
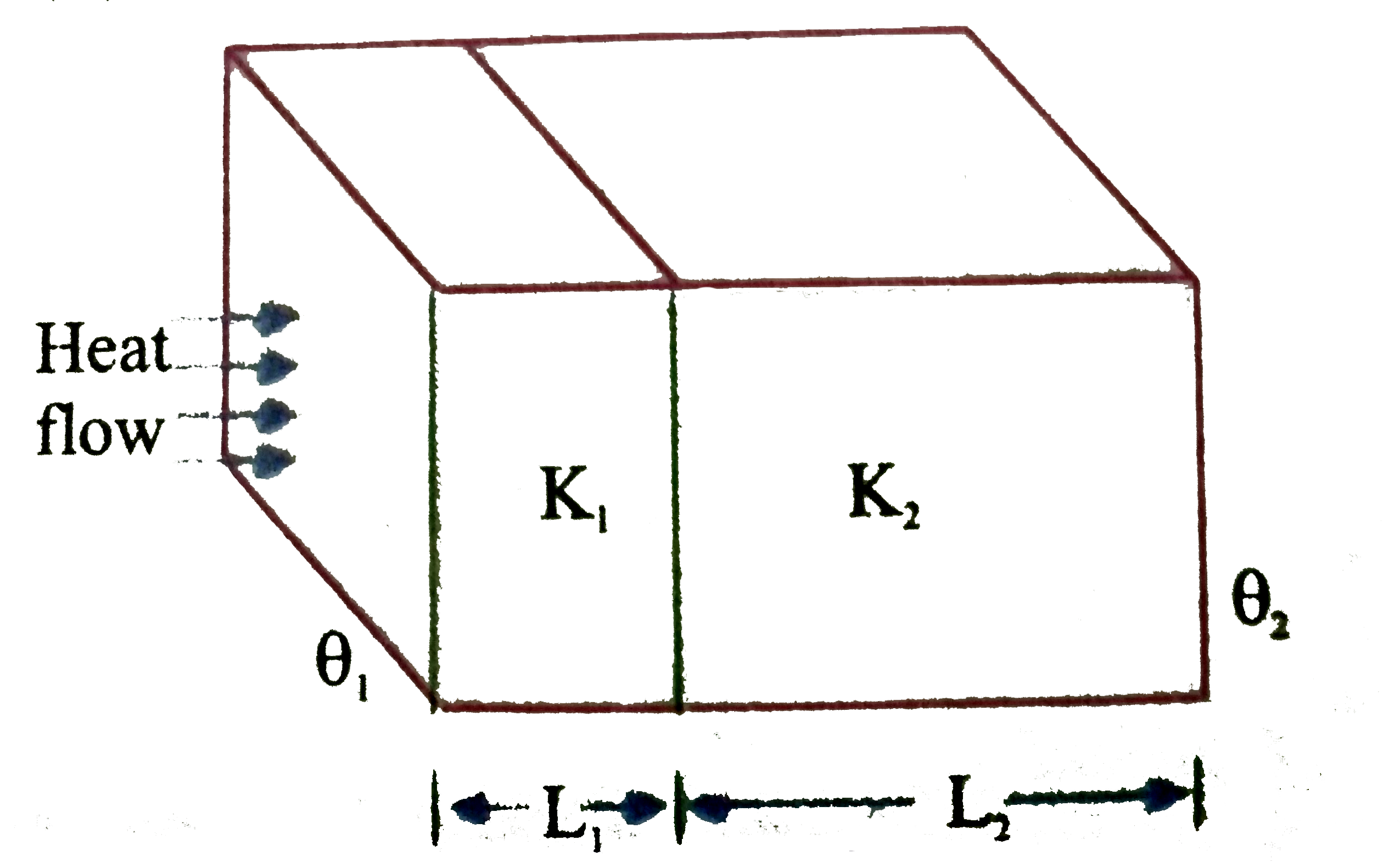
Two plates each of area A thickness L1 and L2 thermal conductivities K1 and K2 respectively are joined to from a single plate of thickness (L1+L2) If the temperatures of the free surfaces are θ1 and θ2 Calculate
(a) Rate of flow of heat
(b) Temperature of interface
 .
.
View SolutionConsider two rods of equal cross - sectionai area A, one of Aluminium and other of iron joined end to end as shown in figure -4.8. Length of the two rods and their thermal coductivities are l1,k1and l2,k2 respectively . If the ends of the rods are maintained at temperature T1 and T2,(T1>T2) find the temperature of the junction in steady state .

View Solution
Knowledge Check
Two walls of thickness d and d and thermal conductivities k and k are in contact. In the steady state, if the temperature at the outer T1 and T2 , the temperature at the common wall is
Ak1T1d2+k2T2d1k1d2+k2d1Bk1T1+k2d2d1+d2C(k1d1+k2d2T1+T2)T1T2Dk1d1T1+k2d2T2k1d1+k2d2If two conducting slabs of thickness d1 and d2, and thermal conductivity K1 and K2 are placed together face to face as shown in figure in the steady state temperature of outer surfaces are θ1 and θ2. The temperature of common surface is-
 AK1θ1d1+K2θ2d2K1d1+K2d2BK1θ1+K2θ2K1+K2CK1θ1+K2θ2θ1+θ2DK1θ1d2+K2θ2d1K1d2+K2d1
AK1θ1d1+K2θ2d2K1d1+K2d2BK1θ1+K2θ2K1+K2CK1θ1+K2θ2θ1+θ2DK1θ1d2+K2θ2d1K1d2+K2d1If two conducting slabs of thickness d1 and d2, and thermal conductivity K1 and K2 are placed together face to face as shown in figure in the steady state temperature of outer surfaces are θ1 and θ2. The temperature of common surface is-
 AK1θ1d1+K2θ2d2K1d1+K2d2BK1θ1+K2θ2K1+K2CK1θ1+K2θ2θ1+θ2DK1θ1d2+K2θ2d1K1d2+K2d1
AK1θ1d1+K2θ2d2K1d1+K2d2BK1θ1+K2θ2K1+K2CK1θ1+K2θ2θ1+θ2DK1θ1d2+K2θ2d1K1d2+K2d1
A composite cylinder is made of two materials having thermal conductivities K1 and K2 as shown. Temperature of the two flat faces of cylinder are maintained at T1 and T2. For what ratio K1/K2 the heat current throught the two materials will be same. Assume steady state and the rod is lagged (insulated from the curved surface).
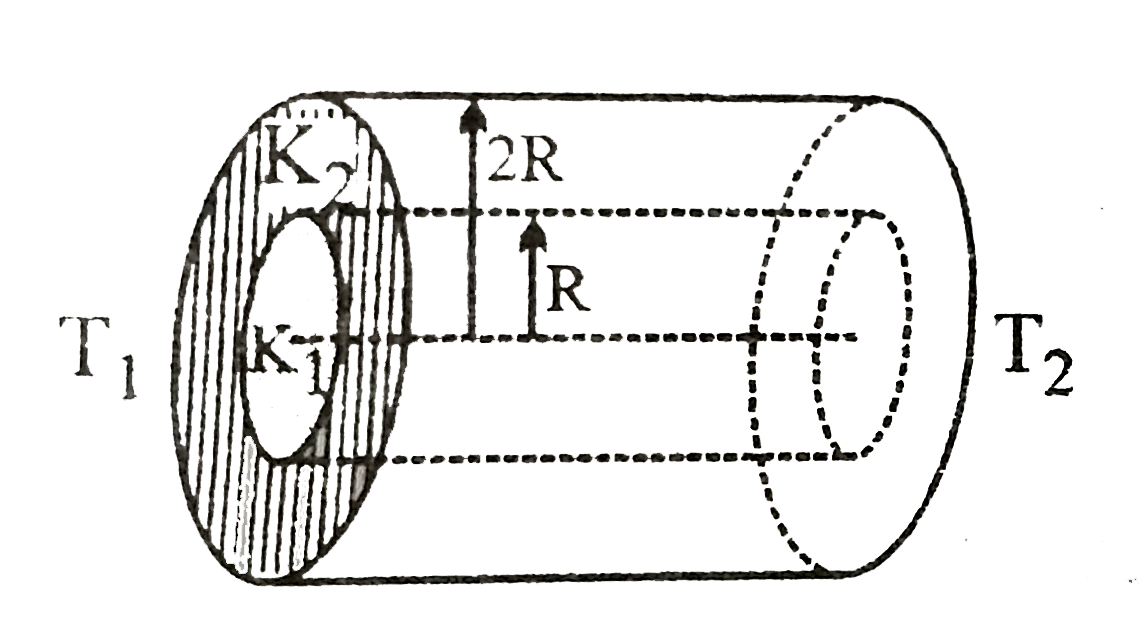
View SolutionTwo bodies of masses m1 and m2 and specific heat capacities S1 and S2 are connected by a rod of length l, cross-ssection area A, thermal conductivity K and negligible heat capacity. The whole system is thermally insulated. At time t=0 , the temperature of the fisrt body is T1 and the temperature of the second body is T2(T2>T1) . Find the temperature difference between the two bodies at time t.
View SolutionThe figure shows the cross-section of the outer wall of a house buit in a hill-resort to keep the house insulated from the freezing temperature of outside. The wall consists of teak wood of thickness L1 and brick of thickness (L2=5L1), sandwitching two layers of an unknown material with identical thermal conductivites and thickness. The thermal conductivity of teak wood is K1 and that of brick is (K2=5K). Heat conducion through the wall has reached a steady state with the temperature of three surfaces being known. (T1=25∘C,T2=20∘C and T5=−20∘C). Find the interface temperature T4 and T3.

View SolutionTwo cylindrical rods of lengths l1 and l2, radii r1 and r2 have thermal conductivities k1 and k2 respectively. The ends of the rods are maintained at the same temperature difference. If l1=2l2 and r1=r2/2, the rates of heat flow in them will be the same if k1/k2 is:
View SolutionTwo bars of same length and same cross-sectional area but of different thermal conductivites K1 and K2 are joined end to end as shown in the figure. One end of the compound bar it is at temperature T1 and the opposite end at temperature T2 (whereT1>T2). The temperature of the junction is

View Solution

