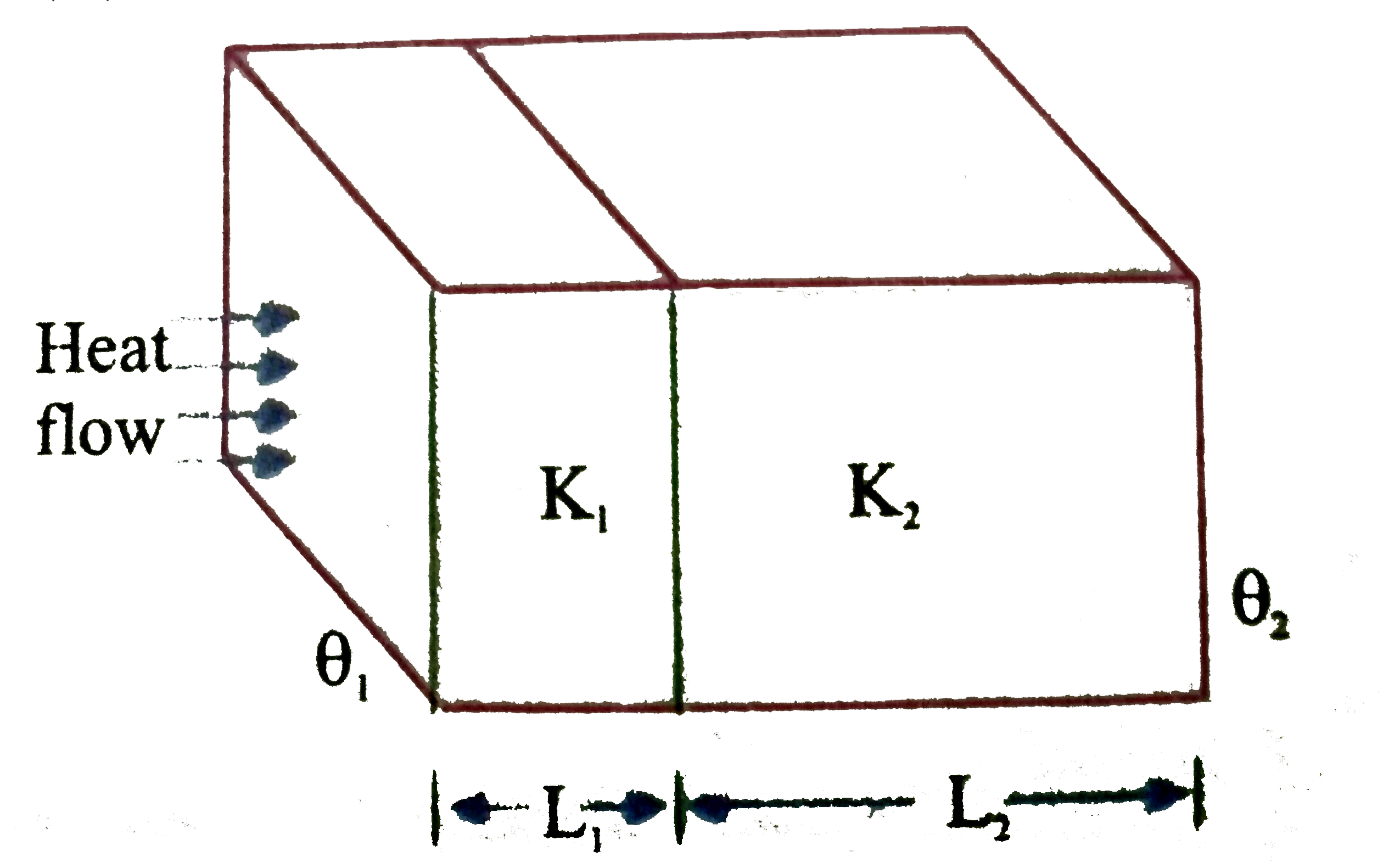
Two plates each of area A thickness L1 and L2 thermal conductivities K1 and K2 respectively are joined to from a single plate of thickness (L1+L2) If the temperatures of the free surfaces are θ1 and θ2 Calculate
(a) Rate of flow of heat
(b) Temperature of interface
 .
.
If the thermal resistance of the two plates are R1 and R2 respectively then as plates are in series
Rs=R1+R2=L1AK1+L2AK2
H=dQdt=ΔθRs=(θ1−θ2)(R1+R2)=A(θ1=θ2)[L1K1+L2K2]
(b) If θ is common temperature of interface then
θ1−θ2R1+R2=θ1−θR−1[∵H1=H2]∴θ=θ1R2+θ2R1(R1+R2)
θ=[θ1L2K2+θ2L1K1][L1K1+L2K2][∵R=LKA] .
Topper's Solved these Questions
- TRANSMISSION OF HEATBOOK - NARAYNACHAPTER - TRANSMISSION OF HEATEXERCISE - C .U .Q
89 Videos
- TRANSMISSION OF HEATBOOK - NARAYNACHAPTER - TRANSMISSION OF HEATEXERCISE - LEVEL -1 (C.W)
1 Videos
- THERMODYNAMICSBOOK - NARAYNACHAPTER - THERMODYNAMICSEXERCISE - Exercise
187 Videos
- UNITS AND MEASUREMENTSBOOK - NARAYNACHAPTER - UNITS AND MEASUREMENTSEXERCISE - STATEMENT TYPE QUESTION
23 Videos
Similar Questions
Two plates eachb of area A, thickness L1andL2 thermal conductivities K1andK2 respectively are joined to form a single plate of thickness (L1+L2). If the temperatures of the free surfaces are T1andT2. Calculate.

(a) rate of flow of heat
(b) temperature of interface and
(c) equivalent thermal conductivity.
View SolutionTwo walls of thicknes l1 and l2 and ther-mal condctivities K1 and K2 are in contact In the steady state, if the temperature at the outer faces are T1 and T2 find the temperature at the common wall .
View Solution
Knowledge Check
If two conducting slabs of thickness d1 and d2, and thermal conductivity K1 and K2 are placed together face to face as shown in figure in the steady state temperature of outer surfaces are θ1 and θ2. The temperature of common surface is-
 AK1θ1d1+K2θ2d2K1d1+K2d2BK1θ1+K2θ2K1+K2CK1θ1+K2θ2θ1+θ2DK1θ1d2+K2θ2d1K1d2+K2d1
AK1θ1d1+K2θ2d2K1d1+K2d2BK1θ1+K2θ2K1+K2CK1θ1+K2θ2θ1+θ2DK1θ1d2+K2θ2d1K1d2+K2d1If two conducting slabs of thickness d1 and d2, and thermal conductivity K1 and K2 are placed together face to face as shown in figure in the steady state temperature of outer surfaces are θ1 and θ2. The temperature of common surface is-
 AK1θ1d1+K2θ2d2K1d1+K2d2BK1θ1+K2θ2K1+K2CK1θ1+K2θ2θ1+θ2DK1θ1d2+K2θ2d1K1d2+K2d1
AK1θ1d1+K2θ2d2K1d1+K2d2BK1θ1+K2θ2K1+K2CK1θ1+K2θ2θ1+θ2DK1θ1d2+K2θ2d1K1d2+K2d1If two metallic plates of equal thickness and thermal conductivities K1 and K2 are put together face to face and a common plate is constructed, then the equivalent thermal conductivity of this plate will be
 AK1K2K1+K2B2K1K2K1+K2C(K21+K22)3/2K1K2D(K21+K22)3/22K1K2
AK1K2K1+K2B2K1K2K1+K2C(K21+K22)3/2K1K2D(K21+K22)3/22K1K2
Two materials having coefficients of thermal conductivity ‘3 K’ and ‘K’ and thickness ‘d’ and ‘3 d’, respectively, are joined to form a slab as shown in the figure. The temperatures of the outer surfaces are θ2 and θ1 respectively, (θ2>θ1) The temperature at the interface is:
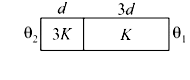
View SolutionA composite slab is prepared by pasting two plates of thickness L1 and L2 and thermal conductivites K1 and K2 . The slab have equal cross-sectional area. Find the equivalent conductivity of the composite slab.
View SolutionIf two metallic plates of equal thickness and equal length and thermal conductivities K1andK2 are put together face to face a common plate is constructed, then the equivalent thermal conductivity of this plate will be-
View SolutionTwo cylindrical rods of lengths l1 and l2, radii r1 and r2 have thermal conductivities k1 and k2 respectively. The ends of the rods are maintained at the same temperature difference. If l1=2l2 and r1=r2/2, the rates of heat flow in them will be the same if k1/k2 is:
View SolutionIf layer thickness L2 is 1.4cm, then its thermal conductivity K2 will have value (in W/mK)
View Solution
