A uniform sphere has radius R. A sphere of diameter R is cut from its edge as shown. Then the distance of centre of mass of remaining portion from the centre of mass of the original sphere is

R/7
R/14
2R/7
R/18
The correct Answer is:B
shift=r3dR3−r3
Topper's Solved these Questions
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level -II(H.W)
Explore 47 Videos
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level-V
Explore 72 Videos
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:NCERT based questions
Explore 15 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - IV
Explore 39 Videos
Similar Questions
A disc of radius a2 is cut out from a uniform disc of radius a as shown in figure . Find the X Coordinate of centre of mass of remaining portion

View SolutionA semicircular portion of radius 'r' is cut from a uniform rectangular plate as shown in figure. The distance of centre of mass 'C' of remaining plate, from point 'O' is
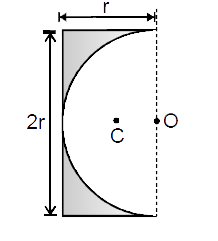
View Solution
Knowledge Check
The distance of the centre of mass of a hemispherical shell of radius R from its centre is
AR2BR3C2R2D2R3A uniform metal dise of radius R is taken and out of it a disc of diameter R is cut off from the end. The centre of the mass of the remaining part will be:
AR4from the centreBR3from the centreCR5 from the centreDR6 from the centreIn the figure one fourth part of a uniform disc of radius R is shown. The distance of the centre of mass of this object from centre 'O' is :
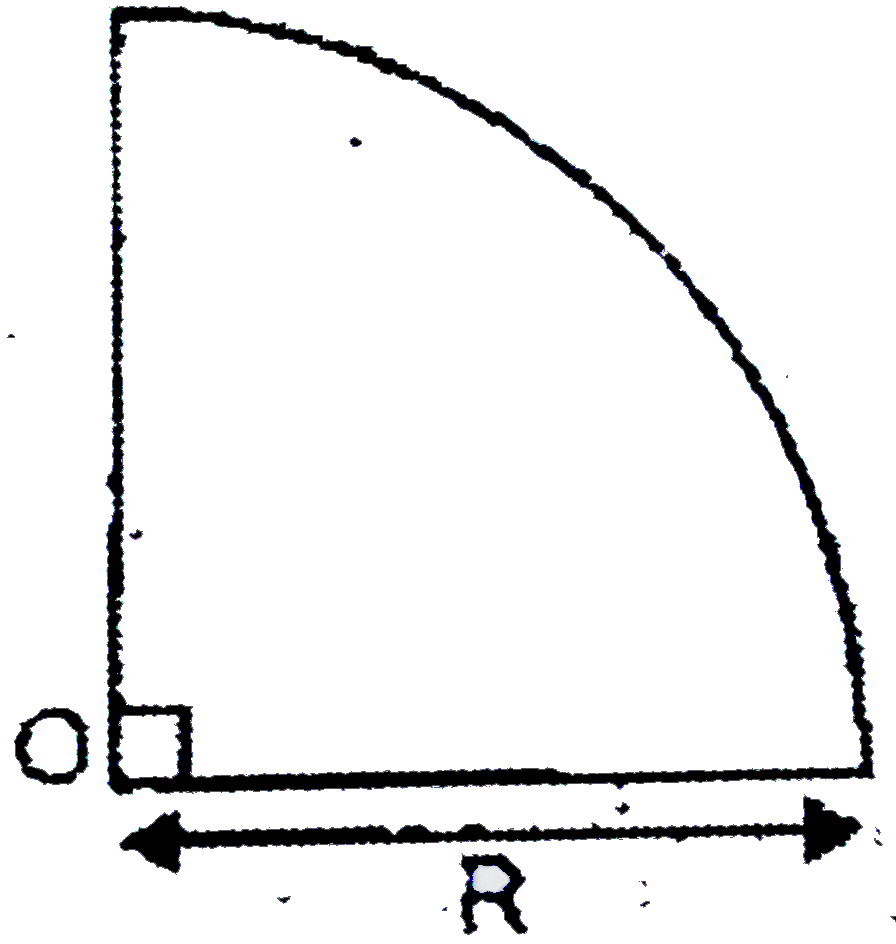 A4R3πB2r3πC√24R3πD√22R3π
A4R3πB2r3πC√24R3πD√22R3π
A particle of mass m is placed at a distance of 4R from the centre of a huge uniform sphere of mass M and radius R. A spherical cavity of diameter R is made in the sphere as shown in the figure. If the gravitational interaction potential energy of the system of mass m and the remaining sphere after making the cavity is λGMm28R. Find the value of λ
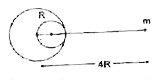
View SolutionA uniform circular disc of radius a is taken. A circular portion of radius b has been removed from it as shown in the figure. If the center of hole is at a distance c from the center of the disc, the distance x2 of the center of mass of the remaining part from the initial center of mass O is given by

View SolutionA solid sphere of mass m & radius R is cut into two equal parts and kept as shown. Find the height of centre of mass from the ground.

View SolutionFrom a circular disc of radius R, a triangular portion is cut (sec figure). The distance of the centre of mass of the remainder from the centre of the disc is −

View SolutionA hemispherical cavity of radius R is created in a solid sphere of radius 2R as shown in the figure . Then y -coordinate of the centre of mass of the remaining sphere is

View Solution

