A uniform rod is 4m long and weights 10kg. If it is supported on a kinetic edge at one meter from the end, what weight placed at that end keeps the rod horizontal.
8kg
10kg
12kg
15kg
The correct Answer is:B
To solve the problem of finding the weight that keeps the rod horizontal, we need to analyze the torque acting on the rod. Here’s the step-by-step solution:
Step 1: Understand the System
We have a uniform rod that is 4 meters long and weighs 10 kg. It is supported at a point that is 1 meter from one end. This means that the distance from the support point to the center of mass of the rod (which is at the midpoint, 2 meters from one end) is 1 meter.
Step 2: Identify Forces and Distances
- Weight of the rod (W_rod) = 10 kg × 9.81 m/s² = 98.1 N (acting downward at the center of the rod, which is 2 meters from the left end).
- Let the weight placed at the end (W) be the unknown force we need to find. This weight will act downward at the right end of the rod (4 meters from the left end).
Step 3: Calculate Torques
To keep the rod horizontal, the sum of the torques about the pivot point (the support point) must be zero.
- Torque due to the weight of the rod (clockwise):
- Distance from the pivot (1 meter from the left end to the center of the rod) = 1 meter.
- Torque (τ_rod) = Weight of the rod × Distance = 98.1 N × 1 m = 98.1 N·m (clockwise).
- Torque due to the weight placed at the end (counterclockwise):
- Distance from the pivot (1 meter from the left end to the right end) = 3 meters.
- Torque (τ_weight) = W × 3 m.
Step 4: Set Up the Equation
For the rod to be in equilibrium (horizontal), the clockwise torque must equal the counterclockwise torque:
τrod=τweight
Substituting the values we have:
98.1N⋅m=W×3m
Step 5: Solve for W
Now, we can solve for W:
W=98.1N⋅m3m=32.7N
Step 6: Convert Weight to Mass
To find the mass equivalent of this weight, we can use the relation W=mg:
m=Wg=32.7N9.81m/s²≈3.33kg
Final Answer
The weight that must be placed at the end of the rod to keep it horizontal is approximately 32.7 N or 3.33 kg.
---
We have a uniform rod that is 4 meters long and weighs 10 kg. It is supported at a point that is 1 meter from one end. This means that the distance from the support point to the center of mass of the rod (which is at the midpoint, 2 meters from one end) is 1 meter.
- Weight of the rod (W_rod) = 10 kg × 9.81 m/s² = 98.1 N (acting downward at the center of the rod, which is 2 meters from the left end).
- Let the weight placed at the end (W) be the unknown force we need to find. This weight will act downward at the right end of the rod (4 meters from the left end).
To keep the rod horizontal, the sum of the torques about the pivot point (the support point) must be zero.
- Distance from the pivot (1 meter from the left end to the center of the rod) = 1 meter.
- Torque (τ_rod) = Weight of the rod × Distance = 98.1 N × 1 m = 98.1 N·m (clockwise).
- Distance from the pivot (1 meter from the left end to the right end) = 3 meters.
- Torque (τ_weight) = W × 3 m.
For the rod to be in equilibrium (horizontal), the clockwise torque must equal the counterclockwise torque:
Now, we can solve for W:
To find the mass equivalent of this weight, we can use the relation W=mg:
The weight that must be placed at the end of the rod to keep it horizontal is approximately 32.7 N or 3.33 kg.
Topper's Solved these Questions
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level -II(H.W)
Explore 47 Videos
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:Level-V
Explore 72 Videos
- SYSTEM OF PARTICLESBook:NARAYNAChapter:SYSTEM OF PARTICLESExercise:NCERT based questions
Explore 15 Videos
- PHYSICAL WORLDBook:NARAYNAChapter:PHYSICAL WORLDExercise:C.U.Q
Explore 10 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTION Book:NARAYNAChapter:SYSTEM OF PARTICLES AND ROTATIONAL MOTION Exercise:EXERCISE - IV
Explore 39 Videos
Similar Questions
A uniform rod AB, 4m long and weighing 12 kg, is supported at end A, with a 6 kg lead weight at B. The rod floats as shown in figure with one-half of its length submerged. The buoyant force on the lead mass is negligible as it is of negligible volume. Find the tension in the cord and the total volume of the rod
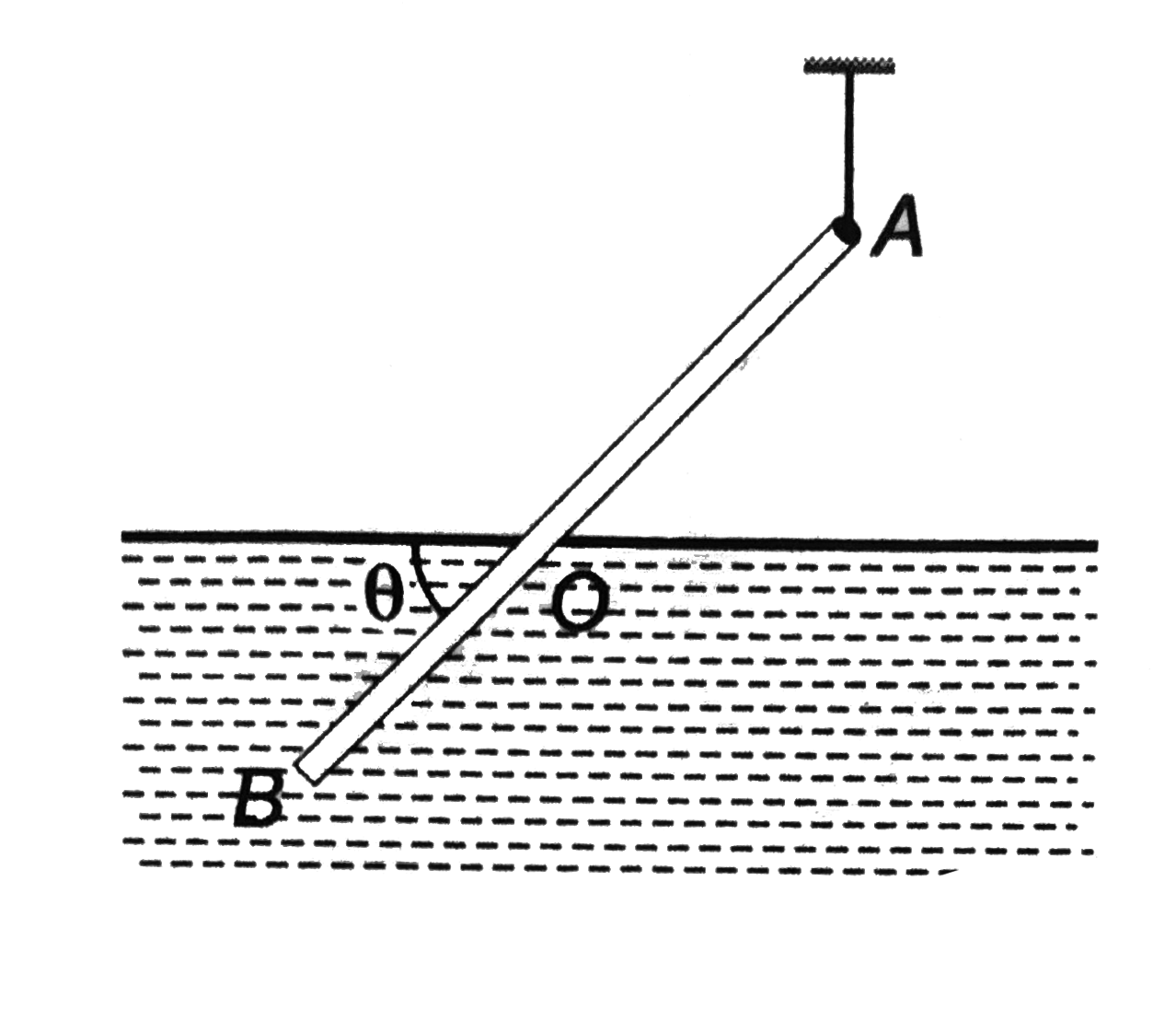
View SolutionA metal bar 70cm long and 4.00kg in mass is supported on two knife edges placed 10cm from each end. A 6.00kg weight is suspended at 30cm from one end. Find the reactions at the knife edges. Assume the bar to be of uniform cross-section and homogeneous.
View Solution
Knowledge Check
A uniform rod of length L and weight WR is suspended as shown in the accompanying figure. A weight W is added to the end of the rod. The rod rests in horizontal position and is hinged at O. the support wire is at an angle θ to the rod. What is the tension T in the wire ?
 AT=WsinθBT=W+WRCT=W+1/2WRDT=W+1/2WRsinθ
AT=WsinθBT=W+WRCT=W+1/2WRDT=W+1/2WRsinθA uniform rod of length L and weight W is suspended horizontally by two vertical ropes as shown. The first rope is attached to the left end of the rod while the second is attached to the left end of the rod while the second rope is attached a distance L/4 from the right end. The tension in the second rope is.
 .AW2BW4CW3D2W3
.AW2BW4CW3D2W3A uniform rod of length 1m mass 4kg is supports on two knife-edges placed 10cm from each end. A 60N weight is suspended at 30cm from one end. The reactions at the knife edges is.
A60 N, 40 NB75 N, 25 NC65 N, 35 ND55 N, 45 N
AS heavy uniform rod is hanging verticallly from a fixed support. It is streetched by its own weight. The diameter of the rod is
View SolutionOne end of a uniform rod of mass M and cross-sectional area A is suspended from a rigid support and an equal mass M is suspended from the other end, what is the stress at the mid point of the rod.
View SolutionA horizontal heavy uniform bar of weight W is supported at its ends by two men. At the instant, one of the men lets go off his end of the rod, the other feels the force on his hand changed to
View SolutionA uniform rod of mass 20 Kg and length 1.6 m is piovted at its end and swings freely in the vertical plane. Angular acceleration of the rod just after the rod is relased from rest in the horizontal position is

View SolutionA uniform one metre long rod AB of weight 17 kg is suspended horizontally from fixed supports by two vertical strings attached to points C and D on the rod at distances of 12 cm and 16 cm from A and B respectively. The strings at C and D can support weights of 10 kg and 9 kg respectively without breaking. Then the position where a weight of 2 kg can be attached to the rod without breaking either of the strings is
View Solution

