A horizontal heavy uniform bar of weight W is supported at its ends by two men. At the instant, one of the men lets go off his end of the rod, the other feels the force on his hand changed to
W
W2
3W4
W4
The correct Answer is:D
To solve the problem, we need to analyze the situation step by step. Let's break it down:
Step 1: Understand the Initial Setup
We have a horizontal uniform bar of weight W supported at both ends by two men (let's call them Man A and Man B). The bar is in equilibrium, meaning the forces acting on it are balanced.
Step 2: Forces Acting on the Bar
Initially, both men exert an upward force on the bar to support its weight. Let the force exerted by Man A be FA and by Man B be FB. Since the bar is uniform, the weight W acts at the center of the bar.
Step 3: Apply the Equilibrium Condition
For the bar to be in equilibrium, the sum of the upward forces must equal the weight of the bar:
FA+FB=W
Step 4: Analyze the Situation When One Man Lets Go
When one of the men (let's say Man A) lets go of his end of the bar, he no longer exerts any force on it. Therefore, the force FA becomes zero.
Step 5: Recalculate the Forces
Now, only Man B is supporting the weight of the bar. The equation for forces now becomes:
FB=W
This means that Man B now has to support the entire weight of the bar alone.
Step 6: Conclusion
Thus, the force felt by Man B on his hand changes to equal the weight of the bar W.
Final Answer
When one man lets go of his end of the rod, the other feels the force on his hand change to W.
---
We have a horizontal uniform bar of weight W supported at both ends by two men (let's call them Man A and Man B). The bar is in equilibrium, meaning the forces acting on it are balanced.
Initially, both men exert an upward force on the bar to support its weight. Let the force exerted by Man A be FA and by Man B be FB. Since the bar is uniform, the weight W acts at the center of the bar.
For the bar to be in equilibrium, the sum of the upward forces must equal the weight of the bar:
FA+FB=W
When one of the men (let's say Man A) lets go of his end of the bar, he no longer exerts any force on it. Therefore, the force FA becomes zero.
Now, only Man B is supporting the weight of the bar. The equation for forces now becomes:
FB=W
This means that Man B now has to support the entire weight of the bar alone.
Thus, the force felt by Man B on his hand changes to equal the weight of the bar W.
When one man lets go of his end of the rod, the other feels the force on his hand change to W.
Topper's Solved these Questions
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on centre of mass)
12 Videos
- ROTATIONAL MOTIONBOOK - ERRORLESS CHAPTER - ROTATIONAL MOTIONEXERCISE - Practice Problems (Problems based on angular displacement, velocity and acceleration)
16 Videos
- NEWTONS LAWS OF MOTIONBOOK - ERRORLESS CHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Self Evaluation Test
16 Videos
- SIMPLE HARMONIC MOTIONBOOK - ERRORLESS CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - simple Harmonic Motion
21 Videos
Similar Questions
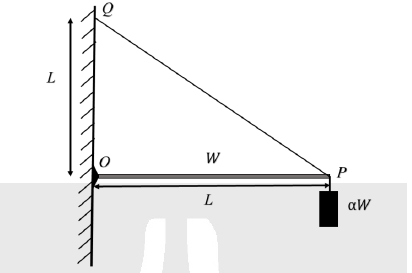
One end of a horizontal uniform beam of weight W and length L is hinged on a vertical wall at point O and its other end is supported by a light inextensible rope. The other end of the rope is fixed at point Q at a height L above the hinge at point O. A block of weight αW is attached at the point Q at a height L above the hinge at point O. A block of weight αW is attached at the point P of the beam as shown in the figure. The rope can sustain a maximum tension of 2(√2)W. Which of the following statements is/are correct?
View SolutionTwo men A and B are carrying a uniform bar of length L on their shoulders. The bar is held horizontally such that A gets one-fourth load. If A is at one end of the bar, the distance of B from that end is
View Solution
Knowledge Check
A uniform rod of length L and weight W is suspended horizontally by two vertical ropes as shown. The first rope is attached to the left end of the rod while the second is attached to the left end of the rod while the second rope is attached a distance L/4 from the right end. The tension in the second rope is.
 .AW2BW4CW3D2W3
.AW2BW4CW3D2W3Two men support a uniform horizontal beam at its two ends, if one of them suddenly lets go, the force exerted by the beam on the other man will
Aremain unaffectedBincreaseCdecreaseDbecome unequal to the force exerted by him on the beamA heavy iron bar of weight W is having its one end on the ground and the other on the shoulder of a man The rod makes an angle θ with the horizontal What is the weight experienced by the man ?
AWsinθBWcosθCWDW/2
One end of a uniform bar of weight w1 is suspended from the roof and a weight w2 is suspended from the other end, the area of cross-section is A. What is the stress at the midpoint of the rod ?
View SolutionOne end of a uniform bar of weight w1 is suspended from the roof and a weight w2 is suspended from the other end, the area of cross-section is A. What is the stress at the midpoint of the rod ?
View SolutionA uniform rod is 4m long and weights 10kg. If it is supported on a kinetic edge at one meter from the end, what weight placed at that end keeps the rod horizontal.
View SolutionA uniform rod of length L and weight WR is suspended as shown in the accompanying figure. A weight W is added to the end of the rod. The rod rests in horizontal position and is hinged at O. the support wire is at an angle θ to the rod. What is the tension T in the wire ?

View SolutionA blacksmith carries a hammer on his shoulder and holds in at the other end of its light handle in his hand. If he changes the point of support of the handle and x is the distance between the point of support and his hand , then the pressure on his hand varies with x as :
View Solution
